3.2实数同步练习 浙教版(2024)数学七年级上册(含答案)
文档属性
| 名称 | 3.2实数同步练习 浙教版(2024)数学七年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 462.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-02 10:06:19 | ||
图片预览
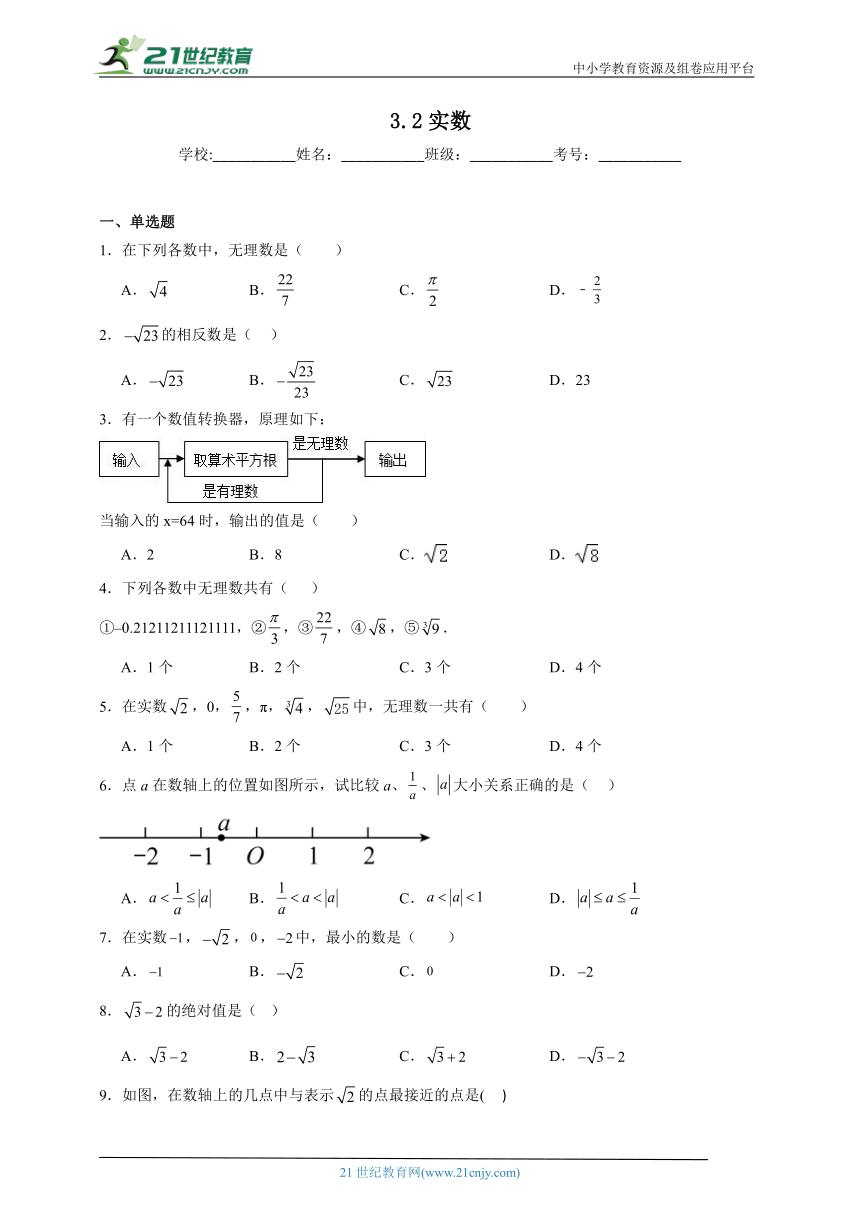


文档简介
中小学教育资源及组卷应用平台
3.2实数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在下列各数中,无理数是( )
A. B. C. D.﹣
2.的相反数是( )
A. B. C. D.23
3.有一个数值转换器,原理如下:
当输入的x=64时,输出的值是( )
A.2 B.8 C. D.
4.下列各数中无理数共有( )
①–0.21211211121111,②,③,④,⑤.
A.1个 B.2个 C.3个 D.4个
5.在实数,0,,π,,中,无理数一共有( )
A.1个 B.2个 C.3个 D.4个
6.点a在数轴上的位置如图所示,试比较a、、大小关系正确的是( )
A. B. C. D.
7.在实数,,,中,最小的数是( )
A. B. C. D.
8.的绝对值是( )
A. B. C. D.
9.如图,在数轴上的几点中与表示的点最接近的点是( )
A.点A B.点B C.点C D.点D
10.下列各数中,绝对值最小的数是( )
A.0 B. C. D.
11.下列实数中最大的数是( )
A. B. C.1 D.
12.在,,,,,(相邻两个之间的个数逐次加),其中无理数的个数为( )
A.个 B.个 C.个 D.个
二、填空题
13.估算: .(结果精确到1)
14.若a=-0.22,b=-2-2,c=(-)-2,d=(-)0,将a,b,c,d按从大到小的顺序用“>”连接起来: .
15. 3 .(选填)
16.以下各数:①﹣1;②;③;④;⑤1.010010001…(相邻两个1之间依次多一个0),其中是无理数的有 .(只填序号)
17.比较大小3 .
三、解答题
18.先阅读下面的文字,再回答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的.因为的整数部分是1,所以将减去其整数部分,所得的差就是的小数部分.例如:,即.的整数部分为2,小数部分为.
(1)的整数部分是______,小数部分是______.
(2)如果的小数部分为的整数部分为,求的值;
(3)已知,其中是整数,且,求的值.
19.小明知道了是无理数,那么在数轴上是否能找到距原点距离为的点呢?小颖在数轴上用尺规作图的方法作出了在数轴上到原点距离等于的点,如图.小颖作图说明了什么?
20.把下列各数填在相应的括号内(填序号):①,②,③,④,⑤,⑥,⑦,⑧(每两个3之间依次多一个2)
(1)整数集合{ …};
(2)分数集合{ …};
(3)无理数集合{ …}.
21.某县在招商引资期间,把已破产的油泵厂出租给外地某投资商.该投资商为了减少固定资产投资,将原来的正方形场地改建成的长方形场地,且长、宽的比为,并且把原来的正方形铁栅栏围墙全部利用,围成新场地的长方形围墙,这些铁栅栏够用吗?
22.某市规划A,B两块空地种植花卉,A空地为正方形,B空地为长与宽之比是的长方形,若两块空地的面积都为,现打算分别在两块空地的四周都围上栅栏,请比较这两块空地所需栅栏长度的大小?并说明理由.
23.先阅读下面材料,再解答问题:
材料:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:若,其中a,b为有理数,是无理数,则.
证明:∵,a为有理数
∴是有理数
∵b为有理数,是无理数
∴
∴
∴
(1)若,其中a、b为有理数,请猜想_________,_________,并根据以上材料证明你的猜想;
(2)已知的整数部分为a,小数部分为b,且x,y为有理数,x,y,a,b满足,求x,y的值.
24.比较与的大小;与的大小;与的大小;猜想与的大小关系,并证明你的结论.
参考答案:
1.C
2.C
3.D
4.C
5.C
6.B
7.D
8.B
9.D
10.A
11.A
12.A
13.5
14.c>d>a>b
15.
16.②⑤③
17.>
18.(1)4,
(2);
(3)的值是.
19.①每一个无理数都可以用数轴上的一个点表示出来,也就是数轴上的点有些表示有理数,有些表示无理数;②到原点距离等于某一个数的实数有两个.
20.(1)④⑤
(2)①③⑥
(3)②⑦⑧
21.围成新场地的长方形围墙时,这些铁栅栏够用
22.B空地所需的栅栏长度比较大
23.(1)3;1
(2)
24.猜想:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.2实数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在下列各数中,无理数是( )
A. B. C. D.﹣
2.的相反数是( )
A. B. C. D.23
3.有一个数值转换器,原理如下:
当输入的x=64时,输出的值是( )
A.2 B.8 C. D.
4.下列各数中无理数共有( )
①–0.21211211121111,②,③,④,⑤.
A.1个 B.2个 C.3个 D.4个
5.在实数,0,,π,,中,无理数一共有( )
A.1个 B.2个 C.3个 D.4个
6.点a在数轴上的位置如图所示,试比较a、、大小关系正确的是( )
A. B. C. D.
7.在实数,,,中,最小的数是( )
A. B. C. D.
8.的绝对值是( )
A. B. C. D.
9.如图,在数轴上的几点中与表示的点最接近的点是( )
A.点A B.点B C.点C D.点D
10.下列各数中,绝对值最小的数是( )
A.0 B. C. D.
11.下列实数中最大的数是( )
A. B. C.1 D.
12.在,,,,,(相邻两个之间的个数逐次加),其中无理数的个数为( )
A.个 B.个 C.个 D.个
二、填空题
13.估算: .(结果精确到1)
14.若a=-0.22,b=-2-2,c=(-)-2,d=(-)0,将a,b,c,d按从大到小的顺序用“>”连接起来: .
15. 3 .(选填)
16.以下各数:①﹣1;②;③;④;⑤1.010010001…(相邻两个1之间依次多一个0),其中是无理数的有 .(只填序号)
17.比较大小3 .
三、解答题
18.先阅读下面的文字,再回答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的.因为的整数部分是1,所以将减去其整数部分,所得的差就是的小数部分.例如:,即.的整数部分为2,小数部分为.
(1)的整数部分是______,小数部分是______.
(2)如果的小数部分为的整数部分为,求的值;
(3)已知,其中是整数,且,求的值.
19.小明知道了是无理数,那么在数轴上是否能找到距原点距离为的点呢?小颖在数轴上用尺规作图的方法作出了在数轴上到原点距离等于的点,如图.小颖作图说明了什么?
20.把下列各数填在相应的括号内(填序号):①,②,③,④,⑤,⑥,⑦,⑧(每两个3之间依次多一个2)
(1)整数集合{ …};
(2)分数集合{ …};
(3)无理数集合{ …}.
21.某县在招商引资期间,把已破产的油泵厂出租给外地某投资商.该投资商为了减少固定资产投资,将原来的正方形场地改建成的长方形场地,且长、宽的比为,并且把原来的正方形铁栅栏围墙全部利用,围成新场地的长方形围墙,这些铁栅栏够用吗?
22.某市规划A,B两块空地种植花卉,A空地为正方形,B空地为长与宽之比是的长方形,若两块空地的面积都为,现打算分别在两块空地的四周都围上栅栏,请比较这两块空地所需栅栏长度的大小?并说明理由.
23.先阅读下面材料,再解答问题:
材料:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:若,其中a,b为有理数,是无理数,则.
证明:∵,a为有理数
∴是有理数
∵b为有理数,是无理数
∴
∴
∴
(1)若,其中a、b为有理数,请猜想_________,_________,并根据以上材料证明你的猜想;
(2)已知的整数部分为a,小数部分为b,且x,y为有理数,x,y,a,b满足,求x,y的值.
24.比较与的大小;与的大小;与的大小;猜想与的大小关系,并证明你的结论.
参考答案:
1.C
2.C
3.D
4.C
5.C
6.B
7.D
8.B
9.D
10.A
11.A
12.A
13.5
14.c>d>a>b
15.
16.②⑤③
17.>
18.(1)4,
(2);
(3)的值是.
19.①每一个无理数都可以用数轴上的一个点表示出来,也就是数轴上的点有些表示有理数,有些表示无理数;②到原点距离等于某一个数的实数有两个.
20.(1)④⑤
(2)①③⑥
(3)②⑦⑧
21.围成新场地的长方形围墙时,这些铁栅栏够用
22.B空地所需的栅栏长度比较大
23.(1)3;1
(2)
24.猜想:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
