浙教版数学九年级上册 第一章 二次函数单元测试(含简单答案)
文档属性
| 名称 | 浙教版数学九年级上册 第一章 二次函数单元测试(含简单答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 326.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-04 00:00:00 | ||
图片预览



文档简介
浙教版数学九年级上册第一章二次函数
一、选择题
1.要得到抛物线 ,可以将抛物线 ( )
A.向左平移2个单位长度,再向上平移3个单位长度
B.向左平移2个单位长度,再向下平移3个单位长度
C.向右平移2个单位长度,再向上平移3个单位长度
D.向右平移2个单位长度,再向下平移3个单位长度.
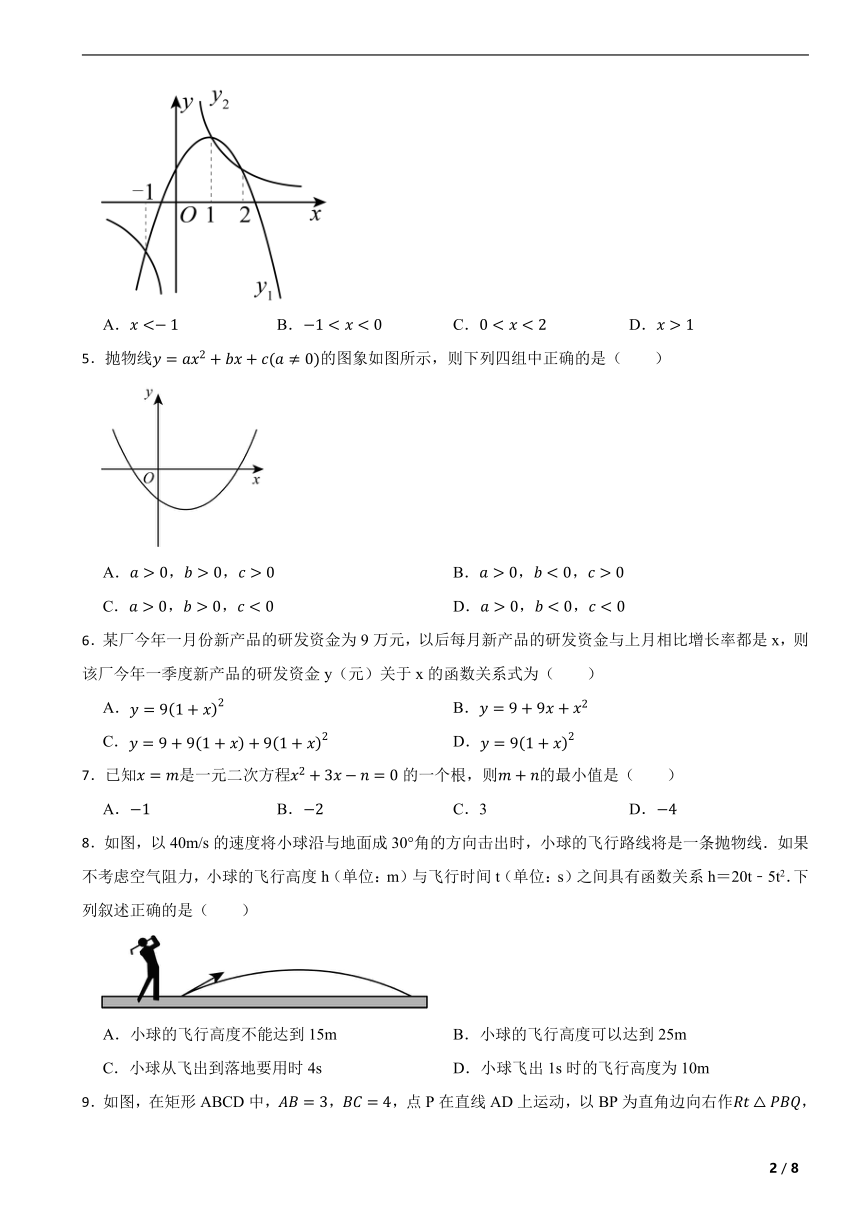
2.在平面直角坐标系中,抛物线如图所示,则关于的方程根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法准确判断
3.函数和(是常数,且在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
4. 函数与的图象如图所示,当( )时,,均随着的增大而减小.
A. B. C. D.
5.抛物线的图象如图所示,则下列四组中正确的是( )
A.,, B.,,
C.,, D.,,
6.某厂今年一月份新产品的研发资金为9万元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年一季度新产品的研发资金y(元)关于x的函数关系式为( )
A. B.
C. D.
7.已知是一元二次方程的一个根,则的最小值是( )
A. B. C.3 D.
8.如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )
A.小球的飞行高度不能达到15m B.小球的飞行高度可以达到25m
C.小球从飞出到落地要用时4s D.小球飞出1s时的飞行高度为10m
9.如图,在矩形ABCD中,,,点P在直线AD上运动,以BP为直角边向右作,使得,,连接CQ,则CQ长的最小值为( )
A. B. C. D.
10.定义:若一次函数的图象与二次函数的图象有两个交点,并且都在坐标轴上,则称二次函数为一次函数的轴点函数.函数(c为常数,)的图象与x轴交于点M,其轴点函数与x轴的另一交点为.若,则的值为( )
A. B.5或 C. D.或3
二、填空题
11.如果函数是关于x的二次函数,则 .
12.若抛物线与x轴有公共点,则k的取值范围是 .
13.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(a,0),那么代数式a2﹣a+2016的值为 .
14.当时,二次函数的最大值是,最小值是,若,则的值是 .
15.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为6米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离是 米.
16.二次函数 的图象如图所示,其对称轴 ,且与x轴交于,点,点P为x轴上一动点,则的最小值为 .
三、解答题
17.如图,已知抛物线经过点.
(1)求出此抛物线的解析式;
(2)当时,直接写出的取值范围.
18.已知二次函数的部分图象如图所示,
(1)求该二次函数图象的对称轴,并利用图象直接写出一元二次方程的解.
(2)向上平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.
19.如图,正方形纸片的边长为4,将它剪去四个全等的直角三角形,得到四边形.设的长为x,四边形的面积为y.
(1)求y关于x的函数表达式;
(2)四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
20.如图所示,在平面直角坐标系中,四边形为正方形,其中点、分别在轴负半轴,轴负半轴上,点在第三象限内,点,点在函数的图象上.
(1)求的值;
(2)连接、,记的面积为,设,求的最大值.
21.已知二次函数的图象与y轴相交于点.
(1)若,求该二次函数的最小值;
(2)若,点都在该函数的图象上,比较和的大小关系;
(3)若点都在该二次函数图象上,分别求的取值范围
22.【综合探究】运用二次函数来研究植物幼苗叶片的生长状况
在大自然里,有很多数学的奥秘.图1是一片美丽的心形叶片,图2是一棵生长的幼苗都可以看作把一条抛物线的一部分沿直线折叠而形成.
【探究一】确定心形叶片的形状
(1)如图3建立平面直角坐标系,心形叶片下部轮廓线可以看作是二次函数图象的一部分,且过原点,求抛物线的解析式及顶点D的坐标;
【探究二】研究心形叶片的宽度:
(2)如图3,心形叶片的对称轴直线与坐标轴交于A,B两点,抛物线与x轴交于另一点C,点,是叶片上的一对对称点,交直线于点.求叶片此处的宽度;
【探究三】探究幼苗叶片的长度
(3)小李同学在观察幼苗生长的过程中,发现幼苗叶片下方轮廓线都可以看作是二次函数图象的一部分;如图4,幼苗叶片下方轮廓线正好对应任务1中的二次函数.已知直线(点P为叶尖)与水平线的夹角为,求幼苗叶片的长度.
23.对某一个函数给出如下定义:对于函数,若当,函数值的取值范围是,且满足则称此函数为“系郡园函数”
(1)已知正比例函数为“1系郡园函数”,则的值为多少?
(2)已知二次函数,当时,是“系郡园函数”,求的取值范围;
(3)已知一次函数(且)为“2系郡园函数”,是函数上的一点,若不论取何值二次函数的图象都不经过点,求满足要求的点的坐标.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】0
12.【答案】
13.【答案】2017
14.【答案】或
15.【答案】
16.【答案】4
17.【答案】(1)
(2)
18.【答案】(1),,
(2)
19.【答案】(1);
(2)当时,y有最小值8,即四边形的面积最小为8.
20.【答案】(1)解:点在函数的图象上,
,
,
即的值为;
(2)解:点在轴负半轴上,
,
四边形为正方形,
,轴,
的面积为,
,
,
抛物线开口向下,
当时,有最大值,的最大值是.
21.【答案】(1)
(2)
(3),
22.【答案】(1),D坐标为;(2);(3)
23.【答案】(1).
(2)
(3),,
1 / 1
一、选择题
1.要得到抛物线 ,可以将抛物线 ( )
A.向左平移2个单位长度,再向上平移3个单位长度
B.向左平移2个单位长度,再向下平移3个单位长度
C.向右平移2个单位长度,再向上平移3个单位长度
D.向右平移2个单位长度,再向下平移3个单位长度.
2.在平面直角坐标系中,抛物线如图所示,则关于的方程根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法准确判断
3.函数和(是常数,且在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
4. 函数与的图象如图所示,当( )时,,均随着的增大而减小.
A. B. C. D.
5.抛物线的图象如图所示,则下列四组中正确的是( )
A.,, B.,,
C.,, D.,,
6.某厂今年一月份新产品的研发资金为9万元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年一季度新产品的研发资金y(元)关于x的函数关系式为( )
A. B.
C. D.
7.已知是一元二次方程的一个根,则的最小值是( )
A. B. C.3 D.
8.如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )
A.小球的飞行高度不能达到15m B.小球的飞行高度可以达到25m
C.小球从飞出到落地要用时4s D.小球飞出1s时的飞行高度为10m
9.如图,在矩形ABCD中,,,点P在直线AD上运动,以BP为直角边向右作,使得,,连接CQ,则CQ长的最小值为( )
A. B. C. D.
10.定义:若一次函数的图象与二次函数的图象有两个交点,并且都在坐标轴上,则称二次函数为一次函数的轴点函数.函数(c为常数,)的图象与x轴交于点M,其轴点函数与x轴的另一交点为.若,则的值为( )
A. B.5或 C. D.或3
二、填空题
11.如果函数是关于x的二次函数,则 .
12.若抛物线与x轴有公共点,则k的取值范围是 .
13.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(a,0),那么代数式a2﹣a+2016的值为 .
14.当时,二次函数的最大值是,最小值是,若,则的值是 .
15.廊桥是我国古老的文化遗产,如图是某座抛物线形的廊桥示意图.已知抛物线的函数表达式为,为保护廊桥的安全,在该抛物线上距水面高为6米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离是 米.
16.二次函数 的图象如图所示,其对称轴 ,且与x轴交于,点,点P为x轴上一动点,则的最小值为 .
三、解答题
17.如图,已知抛物线经过点.
(1)求出此抛物线的解析式;
(2)当时,直接写出的取值范围.
18.已知二次函数的部分图象如图所示,
(1)求该二次函数图象的对称轴,并利用图象直接写出一元二次方程的解.
(2)向上平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.
19.如图,正方形纸片的边长为4,将它剪去四个全等的直角三角形,得到四边形.设的长为x,四边形的面积为y.
(1)求y关于x的函数表达式;
(2)四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
20.如图所示,在平面直角坐标系中,四边形为正方形,其中点、分别在轴负半轴,轴负半轴上,点在第三象限内,点,点在函数的图象上.
(1)求的值;
(2)连接、,记的面积为,设,求的最大值.
21.已知二次函数的图象与y轴相交于点.
(1)若,求该二次函数的最小值;
(2)若,点都在该函数的图象上,比较和的大小关系;
(3)若点都在该二次函数图象上,分别求的取值范围
22.【综合探究】运用二次函数来研究植物幼苗叶片的生长状况
在大自然里,有很多数学的奥秘.图1是一片美丽的心形叶片,图2是一棵生长的幼苗都可以看作把一条抛物线的一部分沿直线折叠而形成.
【探究一】确定心形叶片的形状
(1)如图3建立平面直角坐标系,心形叶片下部轮廓线可以看作是二次函数图象的一部分,且过原点,求抛物线的解析式及顶点D的坐标;
【探究二】研究心形叶片的宽度:
(2)如图3,心形叶片的对称轴直线与坐标轴交于A,B两点,抛物线与x轴交于另一点C,点,是叶片上的一对对称点,交直线于点.求叶片此处的宽度;
【探究三】探究幼苗叶片的长度
(3)小李同学在观察幼苗生长的过程中,发现幼苗叶片下方轮廓线都可以看作是二次函数图象的一部分;如图4,幼苗叶片下方轮廓线正好对应任务1中的二次函数.已知直线(点P为叶尖)与水平线的夹角为,求幼苗叶片的长度.
23.对某一个函数给出如下定义:对于函数,若当,函数值的取值范围是,且满足则称此函数为“系郡园函数”
(1)已知正比例函数为“1系郡园函数”,则的值为多少?
(2)已知二次函数,当时,是“系郡园函数”,求的取值范围;
(3)已知一次函数(且)为“2系郡园函数”,是函数上的一点,若不论取何值二次函数的图象都不经过点,求满足要求的点的坐标.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】D
10.【答案】D
11.【答案】0
12.【答案】
13.【答案】2017
14.【答案】或
15.【答案】
16.【答案】4
17.【答案】(1)
(2)
18.【答案】(1),,
(2)
19.【答案】(1);
(2)当时,y有最小值8,即四边形的面积最小为8.
20.【答案】(1)解:点在函数的图象上,
,
,
即的值为;
(2)解:点在轴负半轴上,
,
四边形为正方形,
,轴,
的面积为,
,
,
抛物线开口向下,
当时,有最大值,的最大值是.
21.【答案】(1)
(2)
(3),
22.【答案】(1),D坐标为;(2);(3)
23.【答案】(1).
(2)
(3),,
1 / 1
同课章节目录
