2.6探索勾股定理（1）

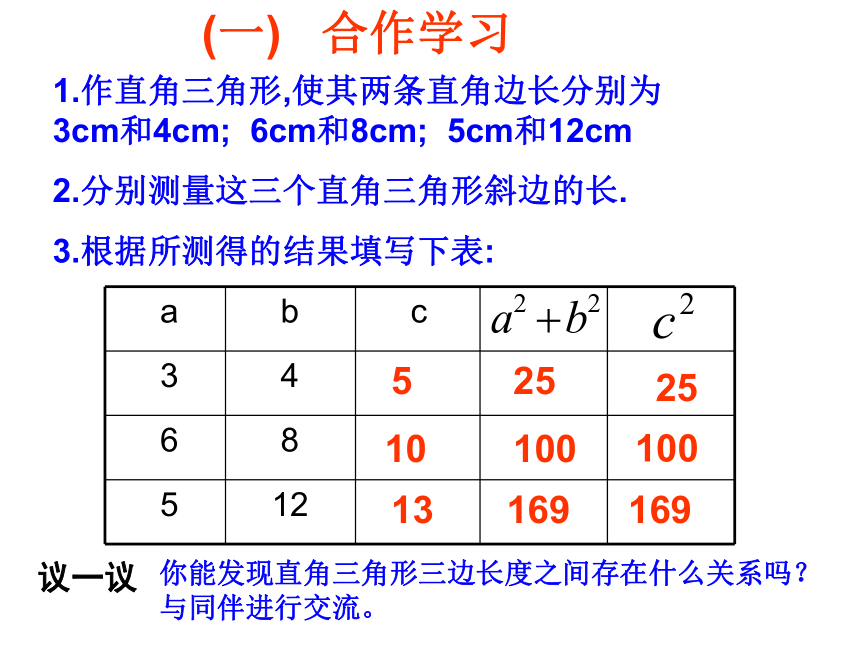
课件21张PPT。2.6勾 股 定 理 (一) 合作学习1.作直角三角形,使其两条直角边长分别为 3cm和4cm; 6cm和8cm; 5cm和12cm
2.分别测量这三个直角三角形斜边的长.
3.根据所测得的结果填写下表:
525251010010013169169议一议你能发现直角三角形三边长度之间存在什么关系吗？
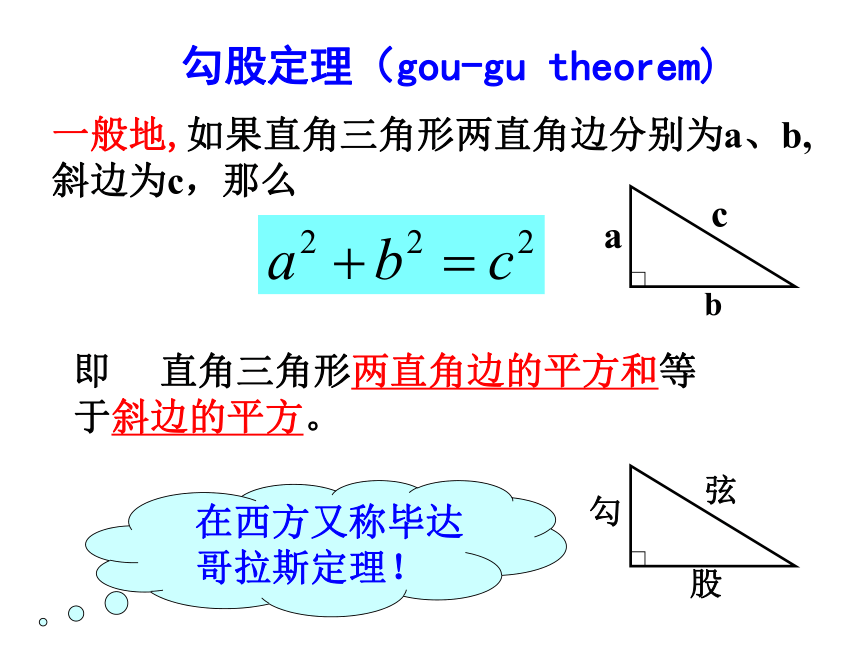
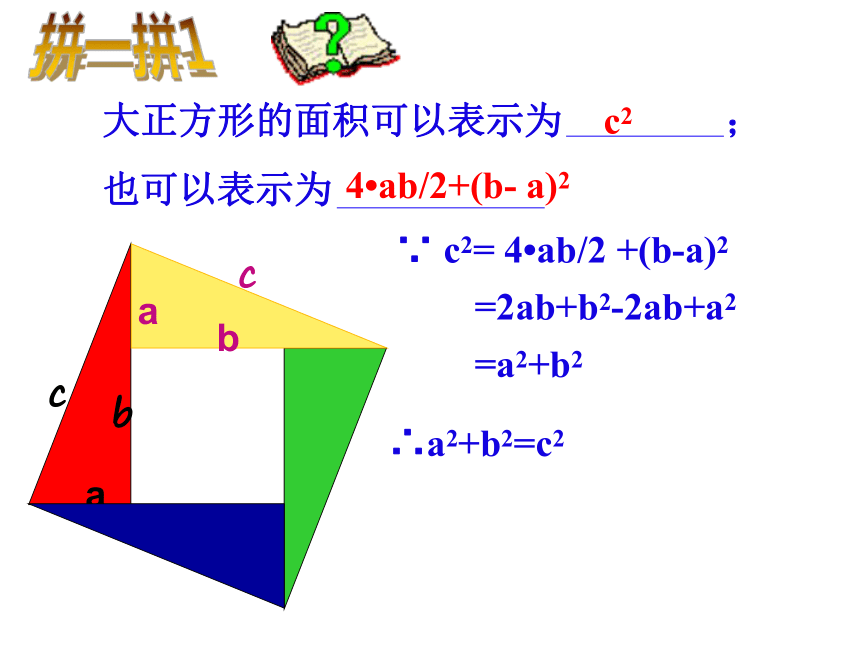
与同伴进行交流。 勾股定理（gou-gu theorem)一般地,如果直角三角形两直角边分别为a、b,斜边为c，那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前 我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。 两千多年前，古希腊有个哥拉 斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派，1955勾 股 世 界 两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。利用拼图来验证勾股定理：1、准备四个全等的直角三角形（设直角三角形的两条直角边分别为a，b，斜边c）；2、你能用这四个直角三角形拼成一个正方形吗？拼一拼试试看3、你拼的正方形中是否含有以斜边c为边的正方形？4、你能否就你拼出的图说明a2+b2=c2？∵ c2= 4?ab/2 +(b-a)2 =2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ；
也可以表示为c24?ab/2+(b- a)2
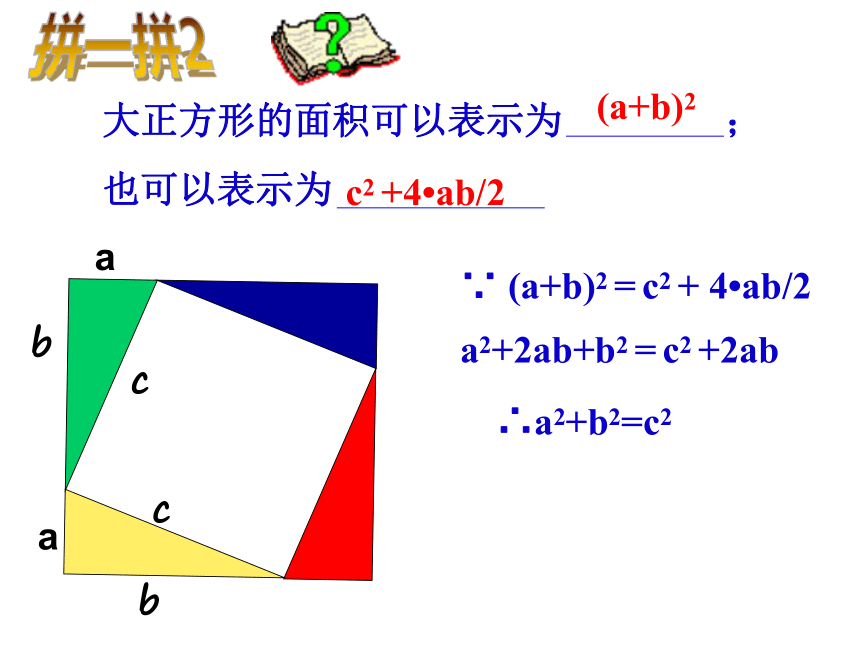
拼一拼1∵ (a+b)2 = c2 + 4?ab/2a2+2ab+b2 = c2 +2ab∴a2+b2=c2大正方形的面积可以表示为 ；
也可以表示为(a+b)2c2 +4?ab/2拼一拼2abcabc例1、已知△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=c
已知: a=2, b=3, 求c;
已知: a=12, c=13, 求b;
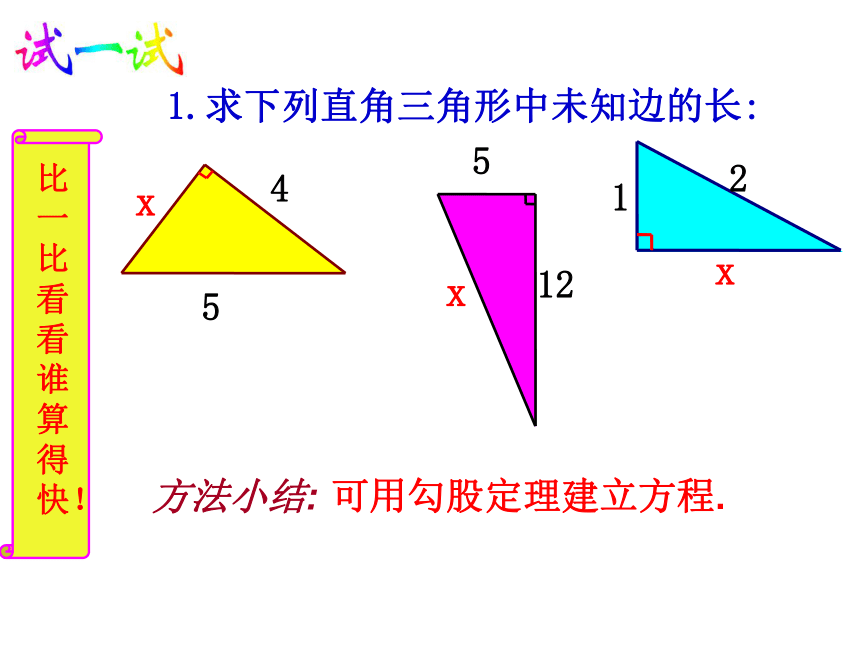
你能用刻度尺和圆规作一条线段,使它的长度为 cm?比一比看看谁算得快！1.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:1x245x125x2、湖的两端有A、Ｂ两点，从与ＢA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )A.50米 B.120米 C.100米 D.130米130120?A 在直角三角形中，已知一条边，以及另两条边之间的关系，求另两条边的长度． 3.在Rt△ABC中，∠C=90o，a、b为直角边,c为斜边，
① 若c=10， a:b=3:4，则a=____，b=____；
② 若a=3，c=b+1，则b=____，c=____；
③ 若b=11，a、c为两个连续的自然数，则a=____，
c=____．注：根据题意，用含一个字母的代数式来表示直角三角形的两条未知边，从而由勾股定理列出方程．６８４５6061C例2、 如图所示是一个长方形零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)算一算!1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做2．如图，所有的四边形都是正方形，所有的三角形
都是直角三角形，其中最大的正方形的边长为7cm,则
正方形A，B，C，D的面积之和为___________cm2。49ADCB1. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少? ABC实践运用! 2.做一个长，宽，高分别为50厘米，40厘米，30厘米的木箱，一根长为70厘米的木棒能否放入，为什么？试用今天学过的知识说明。实践运用!3、在波平如镜的湖面上,有一朵美丽的红莲 ,它高出水面1米 ,一阵微风吹过,红莲被倒向一边,花朵齐及水面,如果知道红莲移动的水平距离为2米 ,问这里水深多少?x+1BCAH12?┓xx2+22=(x+1)2盛开的水莲 小明妈妈买了一部29英寸（74厘米）的电视机，小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了，你同意他的想法吗？你能解释这是为什么？29英寸∴售货员没搞错实践运用!荧屏对角线大约为74厘米4658知识构建:你学会了什么，有什么用途？
　（请与同伴交流） 勾股定理
（a2+b2=c2)布置作业:
1. 课本第40页1，2，3，4题
2. 通过报刊、资料或上网查阅中
外名人对勾股定理的证明方法．美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、
简捷、易懂、明了的证明，就把
这一证法称为“总统”证法。 有趣的总统证法