2024-2025学年浙教版九年级上册数学 第三章 圆的基本性质 单元培优测试卷 (含详解)
文档属性
| 名称 | 2024-2025学年浙教版九年级上册数学 第三章 圆的基本性质 单元培优测试卷 (含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 960.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-05 22:17:10 | ||
图片预览



文档简介
圆的基本性质 单元培优测试卷
一、选择题(每题3分,共30分)
1.如图,分别延长圆内接四边形ABCD的两组对边,延长线相交于点E,F.若∠E=54°41',∠F=43°19',则∠A的度数为( )
第1题图 第2题图 第4题图
A.42° B.41°20' C.41° D.40°20'
2. 如图,中,弦的长为,点在上,,.所在的平面内有一点,若,则点与的位置关系是( )
A.点在上 B.点在内 C.点在外 D.无法确定
3.在平面直角坐标系中,已知点,点在第一象限内,,将绕点逆时针旋转,每次旋转,则第2024次旋转后,点的坐标为( )
A. B. C. D.
4.如图,在半圆O中,直径AB=2,C是半圆上一点,将弧AC沿弦AC折叠交AB于D,点E是弧AD的中点.连接OE,则OE的最小值为( )
A. B. C. D.
5.内接于,过点A作直线EF,已知,根据弦AB的变化,两人分别探究直线EF与的位置关系:
甲:如图1,当弦AB过点O时,EF与相切;
乙:如图2,当弦AB不过点O时,EF也与相切;
第5题图 第6题图 第7题图
下列判断正确的是( )
A.甲对,乙不对 B.甲不对,乙对
C.甲乙都对 D.甲乙都不对
6.如图,等圆和相交于A,B两点,经过的圆心,若,则图中阴影部分的面积为( )
A. B. C. D.
7.如图,正六边形内接于,点P在边上.结论Ⅰ:若的半径为2,P是边的中点,则的长为;结论Ⅱ:连接.若,则的长为,关于结论Ⅰ、Ⅱ,判断正确的是( )
A.只有结论Ⅰ对 B.只有结论Ⅱ对
C.结论Ⅰ、Ⅱ都对 D.结论Ⅰ、Ⅱ都不对
8.已知等腰直角三角形OAC,∠OAC=90°,以O为圆心,OA为半径的圆交OC于点F,过点F作AC的垂线交⊙O于点E,交AC于点B.连结AE,交OC于点D,若OD=,则AB的长为( )
第8题图 第9题图 第10题图
A. B. C. D.
9.如图,在扇形中,平分交于点,点为半径上一动点.若,则阴影部分周长的最小值为( )
A. B. C. D.
10.如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论其中正确的是( )
①∠DBC+∠ADO=90°;②AD2+AC2=4;③若AC=BD,则DE=OE;④若点P为BD的中点,则DE=2OE.
A.①②③ B.①③④ C.②③④ D.①②④
二、填空题(每题4分,共24分)
11.如图,是的半径,是的弦,于点D,是的切线,交的延长线于点E.若,,则线段的长为 .
第11题图 第12题图 第13题图
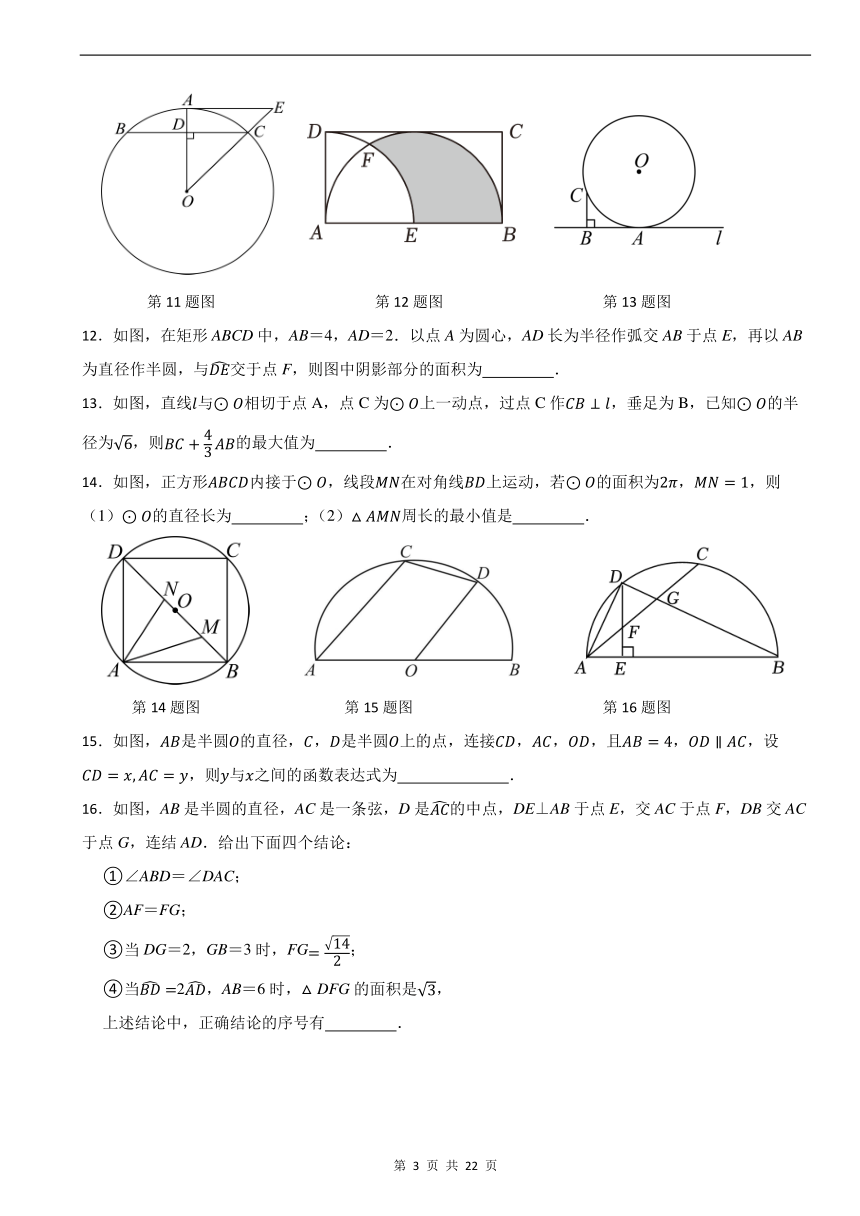
12.如图,在矩形ABCD中,AB=4,AD=2.以点A为圆心,AD长为半径作弧交AB于点E,再以AB为直径作半圆,与交于点F,则图中阴影部分的面积为 .
13.如图,直线与相切于点A,点C为上一动点,过点C作,垂足为B,已知的半径为,则的最大值为 .
14.如图,正方形内接于,线段在对角线上运动,若的面积为,,则(1)的直径长为 ;(2)周长的最小值是 .
第14题图 第15题图 第16题图
15.如图,是半圆的直径,,是半圆上的点,连接,,,且,,设,则与之间的函数表达式为 .
16.如图,AB是半圆的直径,AC是一条弦,D是的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G,连结AD.给出下面四个结论:
①∠ABD=∠DAC;
②AF=FG;
③当DG=2,GB=3时,FG;
④当2,AB=6时,△DFG的面积是,
上述结论中,正确结论的序号有 .
三、综合题(17-19每题6分,20-21每题8分,22题12分,共46分)
17.如图,已知是的半径,过上一点D作弦垂直于,连接,.线段为的直径,连接交于点.
(1)求证:;
(2)若平分,求的值
18.如图,为的直径,是弦,且于点E.连接、、.
(1)求证:;
(2)若,求弦的长.
19.如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为的中点;
(2)若DF=4,AC=16,求⊙O的直径.
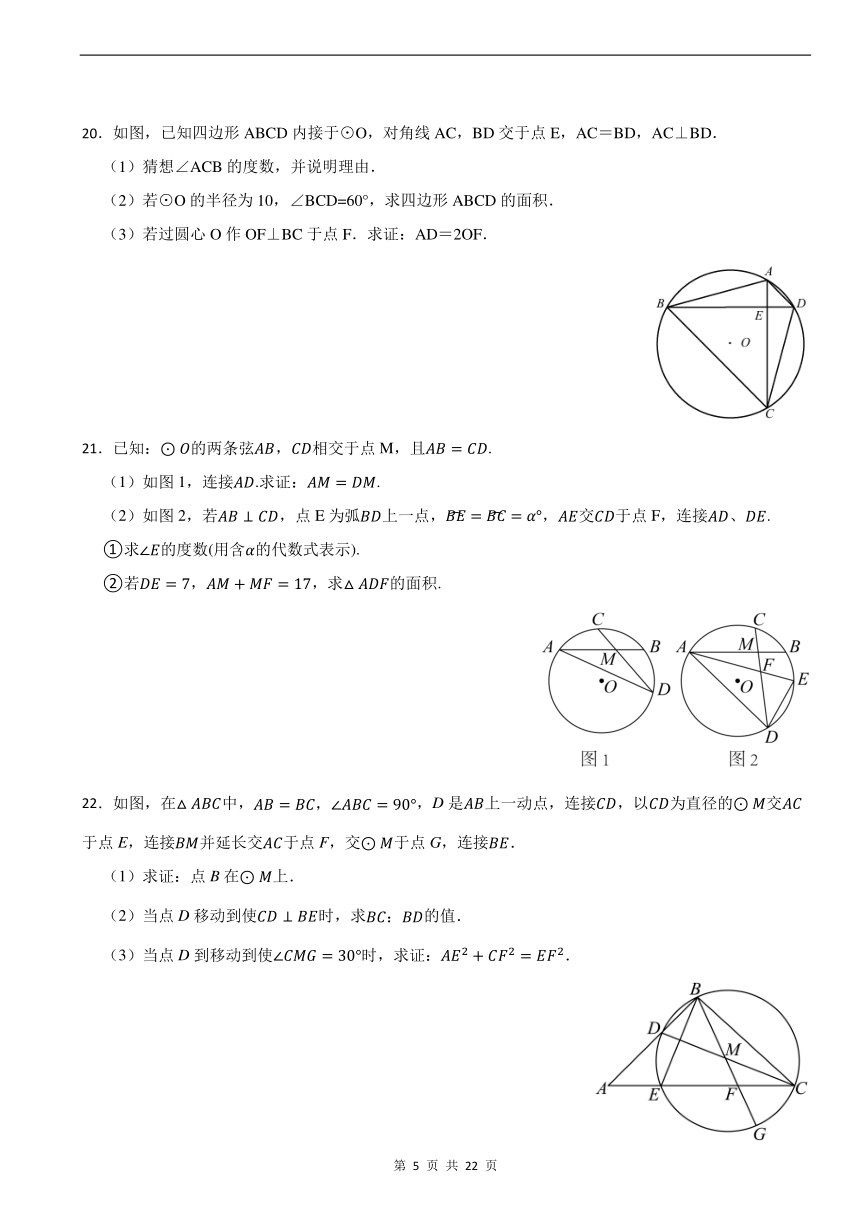
20.如图,已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,AC=BD,AC⊥BD.
(1)猜想∠ACB的度数,并说明理由.
(2)若⊙O的半径为10,∠BCD=60°,求四边形ABCD的面积.
(3)若过圆心O作OF⊥BC于点F.求证:AD=2OF.
21.已知:的两条弦,相交于点M,且.
(1)如图1,连接.求证:.
(2)如图2,若,点E为弧上一点,,交于点F,连接、.
①求的度数(用含的代数式表示).
②若,,求的面积.
22.如图,在中,,D是上一动点,连接,以为直径的交于点E,连接并延长交于点F,交于点G,连接.
(1)求证:点B在上.
(2)当点D移动到使时,求的值.
(3)当点D到移动到使时,求证:.
答案解析部分
1.【答案】C
【解析】【解答】解:∵四边形ABCD内接于圆O,
∴∠A+∠BCD=180°,
∵∠BCD、∠EBC分别是△EBC和△ABF的一个外角,
∠EBC=∠A+∠F,∠BCD=∠E+∠EBC,
∴∠BCD=∠E+∠A+∠F,
∴∠A+∠E+∠A+∠F=180°,
∴2∠A+54°41'+43°19'=180°,
解之:∠A=41°.
故答案为:C.
2.【答案】C
【解析】【解答】解:如图,
∵∠ABC=30°,
∴∠AOC=2∠ABC=60°,
∵OC⊥AB,且,
∴∠ADO=90°,且,
∵sin∠AOC=sin60°=,
∴,
∵OP=5>AO=4,
∴点P在圆O外部.
故答案为:C.
3.【答案】D
【解析】【解答】解:过B作轴于H,
在中,
,
,
,,
由勾股定理得,
,
由题意,可得:,6次一个循环,
,
∴第2024次旋转后,点B的坐标为,
故答案为:D.
4.【答案】A
【解析】【解答】解:连接CO,如图,
由三角形两边之差小于第三边,
当C、O、E共线时,OE最小,
设的弧度为x,则的弧度为180°-x,
∵ ∠CAB=∠CAD,
∴的弧度为180°-x,
由折叠知:==x,
=x-(180°-x)=2x-180°,
∵ 点E为弧AD的中点,
∴==x-90°,
∴=-=90°,
∴所对圆心角为90°,
∵ 直径AB=2,
∴ CE=,
∴OE= CE-OC=.
故答案为:A.
5.【答案】C
【解析】【解答】解:甲:是的直径,
,
,
,
,
,
是半径,
是的切线;
乙:作直径,连接,如图所示:
即(在同圆或等圆中,同弧所对的圆周角相等),
,
,
是的直径,
,
,
,
,
是半径,
是的切线.
故答案为:C
6.【答案】D
7.【答案】C
【解析】【解答】解:如图,连接、,过点D作于点H,
∵六边形为正六边形,
∴,,,,
∴,是等边三角形,
∴,,,
∴,
∵P是边的中点,
∴,
∴,
故结论Ⅰ正确;
设点N是边的中点,连接并延长交于点M,连接,过点D作于点H,设正六边形的边长为a,
∵六边形为正六边形,
∴,,,,,
∴,
由Ⅰ的解答过程可知,,
,,
∴,四边形是矩形,
∴,
∴,
∴,
∴的长为,
故Ⅱ正确,
故答案为:C.
8.【答案】C
【解析】【解答】解:过点O作AE的垂线交BE于点H,连接AH,如图所示:
设的半径为R
∵∠OAC = 90°,OA=AC=R
∴∠O=∠C=45°
∴∠E==22.5°
在Rt△0AC中,由勾股定理得:
OC =
∵OD=
∴CD=OC-OD=
∵EBAC,∠C =45°
∴△BFC为等腰直角三角形,
∴∠BFC= ∠DFE=∠C = 45°
∴∠ADC= ∠E + ∠DFE =22.5°+45°=67.5°
在Rt△ABE中,∠E =22.5°, ∠ABE = 90°
∴∠CAE =90°-∠E=67.5°
∴∠CAE = ∠ADC
∴AC=CD,即R= ,解得:r=,即OA=
∵OHAE
OH是AE的垂直平分线
∴AH = EH
∴∠EAH= ∠E= 22.5°
∴∠HAB = ∠CAE- ∠EAH= 67.5°-22.5°=45°
∴△ABH为等腰直角三角形
∴AB =BH
∴∠OAE= ∠OAC-∠OAE = 90° - 67.5°= 22.5°
.'.∠OAH = ∠OAE + ∠EAH = 45°
∴OHAE,∠EAH=22.5°
∴∠AHO =90°-∠EAH = 90° - 22.5°= 67.5°
∴∠AOH = 180°- ∠OAH- ∠AHO=180°-45°-67.5°= 67.5°
∴∠AHO = ∠AOH = 67.5°
∴AH =OA=,在Rt△ABH中,AB = BH, AH=
由勾股定理得: 即
∴AB=
故答案为:.
9.【答案】A
【解析】【解答】解:由于是定值,要求阴影部分周长的最小值,即求最小值即可
作点关于对称的对称点,连接与直线交于点,则
, ,此时为最小值
连接,
平分,,
,
在中,,
,
阴影部分周长的最小值为.
故答案为:A.
10.【答案】B
【解析】【解答】解:∵AB是⊙O的直径,
∴
∵
∴
∴
∵
∴①正确;
∵
∴
根据条件无法得到②错误;
∵
∴
∴
∵
∴
∴
∴
∵
∴为等边三角形
∵
∴③正确;
若点P为BD的中点, 则
∵
∴
∴
∵O为AB的中点,
∴,
∴④正确;
故答案为:B.
11.【答案】
12.【答案】
【解析】【解答】解:连接AF,EF,过点F作FH⊥AB于点H,
∵以点A为圆心,AD长为半径作弧交AB于点E,
∴AD=AE=AF=2,
∵ 再以AB为直径作半圆,与交于点F,
∴AE=BE=2,AE=EF,
∴AF=AE=EF=2,
∴△AEF是等边三角形,
∴∠FAE=∠AEF=60°,AH=1,
∴FH=AH·tan∠FAE=AH·tan60°=
∴S扇形FAE=,
S弓形AF=,
∴S阴影部分=S半圆AB-S扇形FAE-S弓形AF=
故答案为:.
13.【答案】
14.【答案】;4
15.【答案】
16.【答案】①②③
【解析】【解答】解:如图:连接,
∵是的中点,
∴,
由圆周角定理的推论得:,故①正确;
∵是直径,
∴,
∴,
∵
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,即②正确;
在和,
,
∴,
∴,
即:,
解得:,
由勾股定理得:,
∵,
∴,故③正确;
如图:假设半圆的圆心为O,连接,
∵,,是的中点,
∴
∴,
∵,
∴是等边三角形,
∴,
∴四边形是菱形,
∴,
∵,
∴,即,解得:,
∴,
∵
∴,故④错误.
故答案为:①②③.
17.【答案】(1)证明:∵,
∴,
∴;
(2)解:∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
由(1),
∴,
∵为直径,
∴,
∴,
∴,
∴,
∴,
即.
18.【答案】(1)证明:∵AC是直径,AC⊥BD
∴
∴∠ABD=∠C
又∵OB=OC
∴∠OBC=∠C
∴∠CBO=∠ABD
(2)解:∵AE=4cm,CE=16cm
∴直径AC=AE+CE=20cm
∴OA=OB=10cm
∴OE=OA-AE=10-4=6cm
∵AC是直径,AC⊥BD
∴BE=ED= cm
∴BD=2BE=16cm
19.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=90°,
∴OF⊥AC,
∴ = ,
即点D为 的中点;
(2)解:OF⊥AC,
∴AF= AC=8,
∵DF=4,
∴OF=OD DF=OA 4,
∵OA2=AF2+OF2,
∴OA2=82+(OA 4)2,
∴OA=10,
∴⊙O的直径为20.
20.【答案】(1)解:∠ACB=45°,理由如下:
∵AC⊥BD,
∴∠AEB=90°.
∴∠ABE+∠BAE=90°.
∴=180°.
∴=180°.
∵AC=BD,
∴.
∴.
∴.
∴=90°.
∴∠ACB=45°.
(2)解:如图,连结BO,DO,过点作交BD于点.
在Rt中,,
(3)证明:如图,延长BO交⊙O于点M,连结CM,DM.
∵OF⊥BC,
∴BF=CF,即点F是BC的中点.
又∵点O是BM的中点,
∴OF是△BCM的中位线.
∴CM=2OF.
∵DM⊥BD,AC⊥BD,
∴DM∥AC.
∴AD=CM.
∴AD=2OF.
21.【答案】(1)证明:如图1,
∵,
∴,即,
∴,
∴,
∴;
(2)解:①.
理由如下:
连接,如图,
∵,
∴,
∵,
∴,
∴;
②∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,解得,
∴,
∴.
22.【答案】(1)证明:根据题意得,
∵,
∴,
∴,
∴点B在上.
(2)解:连接,如图,
∵,为直径,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
(3)证明:过点B作,过点A作,交于点N,连接,
∵,
∴,
∴,
∵M为的中点,
∴,
∵,
∴,,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
在中,,
∴.
一、选择题(每题3分,共30分)
1.如图,分别延长圆内接四边形ABCD的两组对边,延长线相交于点E,F.若∠E=54°41',∠F=43°19',则∠A的度数为( )
第1题图 第2题图 第4题图
A.42° B.41°20' C.41° D.40°20'
2. 如图,中,弦的长为,点在上,,.所在的平面内有一点,若,则点与的位置关系是( )
A.点在上 B.点在内 C.点在外 D.无法确定
3.在平面直角坐标系中,已知点,点在第一象限内,,将绕点逆时针旋转,每次旋转,则第2024次旋转后,点的坐标为( )
A. B. C. D.
4.如图,在半圆O中,直径AB=2,C是半圆上一点,将弧AC沿弦AC折叠交AB于D,点E是弧AD的中点.连接OE,则OE的最小值为( )
A. B. C. D.
5.内接于,过点A作直线EF,已知,根据弦AB的变化,两人分别探究直线EF与的位置关系:
甲:如图1,当弦AB过点O时,EF与相切;
乙:如图2,当弦AB不过点O时,EF也与相切;
第5题图 第6题图 第7题图
下列判断正确的是( )
A.甲对,乙不对 B.甲不对,乙对
C.甲乙都对 D.甲乙都不对
6.如图,等圆和相交于A,B两点,经过的圆心,若,则图中阴影部分的面积为( )
A. B. C. D.
7.如图,正六边形内接于,点P在边上.结论Ⅰ:若的半径为2,P是边的中点,则的长为;结论Ⅱ:连接.若,则的长为,关于结论Ⅰ、Ⅱ,判断正确的是( )
A.只有结论Ⅰ对 B.只有结论Ⅱ对
C.结论Ⅰ、Ⅱ都对 D.结论Ⅰ、Ⅱ都不对
8.已知等腰直角三角形OAC,∠OAC=90°,以O为圆心,OA为半径的圆交OC于点F,过点F作AC的垂线交⊙O于点E,交AC于点B.连结AE,交OC于点D,若OD=,则AB的长为( )
第8题图 第9题图 第10题图
A. B. C. D.
9.如图,在扇形中,平分交于点,点为半径上一动点.若,则阴影部分周长的最小值为( )
A. B. C. D.
10.如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论其中正确的是( )
①∠DBC+∠ADO=90°;②AD2+AC2=4;③若AC=BD,则DE=OE;④若点P为BD的中点,则DE=2OE.
A.①②③ B.①③④ C.②③④ D.①②④
二、填空题(每题4分,共24分)
11.如图,是的半径,是的弦,于点D,是的切线,交的延长线于点E.若,,则线段的长为 .
第11题图 第12题图 第13题图
12.如图,在矩形ABCD中,AB=4,AD=2.以点A为圆心,AD长为半径作弧交AB于点E,再以AB为直径作半圆,与交于点F,则图中阴影部分的面积为 .
13.如图,直线与相切于点A,点C为上一动点,过点C作,垂足为B,已知的半径为,则的最大值为 .
14.如图,正方形内接于,线段在对角线上运动,若的面积为,,则(1)的直径长为 ;(2)周长的最小值是 .
第14题图 第15题图 第16题图
15.如图,是半圆的直径,,是半圆上的点,连接,,,且,,设,则与之间的函数表达式为 .
16.如图,AB是半圆的直径,AC是一条弦,D是的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G,连结AD.给出下面四个结论:
①∠ABD=∠DAC;
②AF=FG;
③当DG=2,GB=3时,FG;
④当2,AB=6时,△DFG的面积是,
上述结论中,正确结论的序号有 .
三、综合题(17-19每题6分,20-21每题8分,22题12分,共46分)
17.如图,已知是的半径,过上一点D作弦垂直于,连接,.线段为的直径,连接交于点.
(1)求证:;
(2)若平分,求的值
18.如图,为的直径,是弦,且于点E.连接、、.
(1)求证:;
(2)若,求弦的长.
19.如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为的中点;
(2)若DF=4,AC=16,求⊙O的直径.
20.如图,已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,AC=BD,AC⊥BD.
(1)猜想∠ACB的度数,并说明理由.
(2)若⊙O的半径为10,∠BCD=60°,求四边形ABCD的面积.
(3)若过圆心O作OF⊥BC于点F.求证:AD=2OF.
21.已知:的两条弦,相交于点M,且.
(1)如图1,连接.求证:.
(2)如图2,若,点E为弧上一点,,交于点F,连接、.
①求的度数(用含的代数式表示).
②若,,求的面积.
22.如图,在中,,D是上一动点,连接,以为直径的交于点E,连接并延长交于点F,交于点G,连接.
(1)求证:点B在上.
(2)当点D移动到使时,求的值.
(3)当点D到移动到使时,求证:.
答案解析部分
1.【答案】C
【解析】【解答】解:∵四边形ABCD内接于圆O,
∴∠A+∠BCD=180°,
∵∠BCD、∠EBC分别是△EBC和△ABF的一个外角,
∠EBC=∠A+∠F,∠BCD=∠E+∠EBC,
∴∠BCD=∠E+∠A+∠F,
∴∠A+∠E+∠A+∠F=180°,
∴2∠A+54°41'+43°19'=180°,
解之:∠A=41°.
故答案为:C.
2.【答案】C
【解析】【解答】解:如图,
∵∠ABC=30°,
∴∠AOC=2∠ABC=60°,
∵OC⊥AB,且,
∴∠ADO=90°,且,
∵sin∠AOC=sin60°=,
∴,
∵OP=5>AO=4,
∴点P在圆O外部.
故答案为:C.
3.【答案】D
【解析】【解答】解:过B作轴于H,
在中,
,
,
,,
由勾股定理得,
,
由题意,可得:,6次一个循环,
,
∴第2024次旋转后,点B的坐标为,
故答案为:D.
4.【答案】A
【解析】【解答】解:连接CO,如图,
由三角形两边之差小于第三边,
当C、O、E共线时,OE最小,
设的弧度为x,则的弧度为180°-x,
∵ ∠CAB=∠CAD,
∴的弧度为180°-x,
由折叠知:==x,
=x-(180°-x)=2x-180°,
∵ 点E为弧AD的中点,
∴==x-90°,
∴=-=90°,
∴所对圆心角为90°,
∵ 直径AB=2,
∴ CE=,
∴OE= CE-OC=.
故答案为:A.
5.【答案】C
【解析】【解答】解:甲:是的直径,
,
,
,
,
,
是半径,
是的切线;
乙:作直径,连接,如图所示:
即(在同圆或等圆中,同弧所对的圆周角相等),
,
,
是的直径,
,
,
,
,
是半径,
是的切线.
故答案为:C
6.【答案】D
7.【答案】C
【解析】【解答】解:如图,连接、,过点D作于点H,
∵六边形为正六边形,
∴,,,,
∴,是等边三角形,
∴,,,
∴,
∵P是边的中点,
∴,
∴,
故结论Ⅰ正确;
设点N是边的中点,连接并延长交于点M,连接,过点D作于点H,设正六边形的边长为a,
∵六边形为正六边形,
∴,,,,,
∴,
由Ⅰ的解答过程可知,,
,,
∴,四边形是矩形,
∴,
∴,
∴,
∴的长为,
故Ⅱ正确,
故答案为:C.
8.【答案】C
【解析】【解答】解:过点O作AE的垂线交BE于点H,连接AH,如图所示:
设的半径为R
∵∠OAC = 90°,OA=AC=R
∴∠O=∠C=45°
∴∠E==22.5°
在Rt△0AC中,由勾股定理得:
OC =
∵OD=
∴CD=OC-OD=
∵EBAC,∠C =45°
∴△BFC为等腰直角三角形,
∴∠BFC= ∠DFE=∠C = 45°
∴∠ADC= ∠E + ∠DFE =22.5°+45°=67.5°
在Rt△ABE中,∠E =22.5°, ∠ABE = 90°
∴∠CAE =90°-∠E=67.5°
∴∠CAE = ∠ADC
∴AC=CD,即R= ,解得:r=,即OA=
∵OHAE
OH是AE的垂直平分线
∴AH = EH
∴∠EAH= ∠E= 22.5°
∴∠HAB = ∠CAE- ∠EAH= 67.5°-22.5°=45°
∴△ABH为等腰直角三角形
∴AB =BH
∴∠OAE= ∠OAC-∠OAE = 90° - 67.5°= 22.5°
.'.∠OAH = ∠OAE + ∠EAH = 45°
∴OHAE,∠EAH=22.5°
∴∠AHO =90°-∠EAH = 90° - 22.5°= 67.5°
∴∠AOH = 180°- ∠OAH- ∠AHO=180°-45°-67.5°= 67.5°
∴∠AHO = ∠AOH = 67.5°
∴AH =OA=,在Rt△ABH中,AB = BH, AH=
由勾股定理得: 即
∴AB=
故答案为:.
9.【答案】A
【解析】【解答】解:由于是定值,要求阴影部分周长的最小值,即求最小值即可
作点关于对称的对称点,连接与直线交于点,则
, ,此时为最小值
连接,
平分,,
,
在中,,
,
阴影部分周长的最小值为.
故答案为:A.
10.【答案】B
【解析】【解答】解:∵AB是⊙O的直径,
∴
∵
∴
∴
∵
∴①正确;
∵
∴
根据条件无法得到②错误;
∵
∴
∴
∵
∴
∴
∴
∵
∴为等边三角形
∵
∴③正确;
若点P为BD的中点, 则
∵
∴
∴
∵O为AB的中点,
∴,
∴④正确;
故答案为:B.
11.【答案】
12.【答案】
【解析】【解答】解:连接AF,EF,过点F作FH⊥AB于点H,
∵以点A为圆心,AD长为半径作弧交AB于点E,
∴AD=AE=AF=2,
∵ 再以AB为直径作半圆,与交于点F,
∴AE=BE=2,AE=EF,
∴AF=AE=EF=2,
∴△AEF是等边三角形,
∴∠FAE=∠AEF=60°,AH=1,
∴FH=AH·tan∠FAE=AH·tan60°=
∴S扇形FAE=,
S弓形AF=,
∴S阴影部分=S半圆AB-S扇形FAE-S弓形AF=
故答案为:.
13.【答案】
14.【答案】;4
15.【答案】
16.【答案】①②③
【解析】【解答】解:如图:连接,
∵是的中点,
∴,
由圆周角定理的推论得:,故①正确;
∵是直径,
∴,
∴,
∵
∴,
∵,
∴,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,即②正确;
在和,
,
∴,
∴,
即:,
解得:,
由勾股定理得:,
∵,
∴,故③正确;
如图:假设半圆的圆心为O,连接,
∵,,是的中点,
∴
∴,
∵,
∴是等边三角形,
∴,
∴四边形是菱形,
∴,
∵,
∴,即,解得:,
∴,
∵
∴,故④错误.
故答案为:①②③.
17.【答案】(1)证明:∵,
∴,
∴;
(2)解:∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
由(1),
∴,
∵为直径,
∴,
∴,
∴,
∴,
∴,
即.
18.【答案】(1)证明:∵AC是直径,AC⊥BD
∴
∴∠ABD=∠C
又∵OB=OC
∴∠OBC=∠C
∴∠CBO=∠ABD
(2)解:∵AE=4cm,CE=16cm
∴直径AC=AE+CE=20cm
∴OA=OB=10cm
∴OE=OA-AE=10-4=6cm
∵AC是直径,AC⊥BD
∴BE=ED= cm
∴BD=2BE=16cm
19.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=90°,
∴OF⊥AC,
∴ = ,
即点D为 的中点;
(2)解:OF⊥AC,
∴AF= AC=8,
∵DF=4,
∴OF=OD DF=OA 4,
∵OA2=AF2+OF2,
∴OA2=82+(OA 4)2,
∴OA=10,
∴⊙O的直径为20.
20.【答案】(1)解:∠ACB=45°,理由如下:
∵AC⊥BD,
∴∠AEB=90°.
∴∠ABE+∠BAE=90°.
∴=180°.
∴=180°.
∵AC=BD,
∴.
∴.
∴.
∴=90°.
∴∠ACB=45°.
(2)解:如图,连结BO,DO,过点作交BD于点.
在Rt中,,
(3)证明:如图,延长BO交⊙O于点M,连结CM,DM.
∵OF⊥BC,
∴BF=CF,即点F是BC的中点.
又∵点O是BM的中点,
∴OF是△BCM的中位线.
∴CM=2OF.
∵DM⊥BD,AC⊥BD,
∴DM∥AC.
∴AD=CM.
∴AD=2OF.
21.【答案】(1)证明:如图1,
∵,
∴,即,
∴,
∴,
∴;
(2)解:①.
理由如下:
连接,如图,
∵,
∴,
∵,
∴,
∴;
②∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,解得,
∴,
∴.
22.【答案】(1)证明:根据题意得,
∵,
∴,
∴,
∴点B在上.
(2)解:连接,如图,
∵,为直径,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
(3)证明:过点B作,过点A作,交于点N,连接,
∵,
∴,
∴,
∵M为的中点,
∴,
∵,
∴,,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
在中,,
∴.
同课章节目录
