4.3整式同步练习 浙教版(2024)数学七年级上册(含答案)
文档属性
| 名称 | 4.3整式同步练习 浙教版(2024)数学七年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 675.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
4.3整式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.是二次三项式 B.是单项式
C.的次数是8 D.的系数是
2.如图所示:用黑白两种颜色的正五边形地砖按下图所示的规律,拼成若干个蝴蝶图案,则第7幅蝴蝶图案中白色地砖有( )
A.35块 B.27块 C.22块 D.7块
3.多项式的次数为( )
A.8 B.5 C.3 D.2
4.当时,的值为,则的值为( )
A. B.9 C.3 D.-4
5.将正整数按如图所示的规律排列下去,若有序实数对表示第排,从左到右第个数,如表示9,则表示2022的有序数对是( )
A. B. C. D.
6.下列图形都是由同样大小的五角星按照一定规律所组成的,其中第①个图形中一共有个五角星,第②个图形中一共有个五角星,第③个图形中一共有个五角星,第④个图形中一共有个五角星,,按此规律排列下去,第⑧个图形中五角星的个数为( )
A. B. C. D.
7.下列式子是单项式的是( )
A. B. C. D.
8.多项式的常数项为( )
A. B. C. D.
9.多项式3x3﹣2x2y2+x+3是( )
A.三次四项式 B.四次四项式 C.三次三项式 D.四次三项式
10.已知有一个有序数组,按下列方式重新写成数组,使得,,,,接着按同样的方式重新写成数组,使得,,,,按照这个规律继续写下去,若有一个数组满足,则n的值为( )
A.9 B.10 C.11 D.12
11.定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则: 若n=13,则第2020次“F”运算的结果是( )
A.1 B.4 C.2020 D.42020
12.如图,正方形的边长为1个单位长度,电子蚂蚁从点A出发以1个单位/秒的速度顺时针绕正方形运动,同时电子蚂蚁从点A出发以3个单位/秒的速度逆时针绕正方形运动,则第2024次相遇在( )
A.点A B.点 C.点 D.点
二、填空题
13.单项式次数是 ,系数是 .
14.将一列有理数,如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数 ,应排在A、B、C、D、E中 的位置.
……
15.如图,将第一个图(图①)所示的正三角形连接各边中点进行分割,得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,……,则得到的第五个图中,共有 个正三角形.
16.代数式﹣的系数是 ,次数为 .
17.观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球 个.
三、解答题
18.探索规律:观察下面由※组成的图案和算式,解答问题:
(1)请猜想:__________;
(2)__________;
(3)请用上述规律计算:
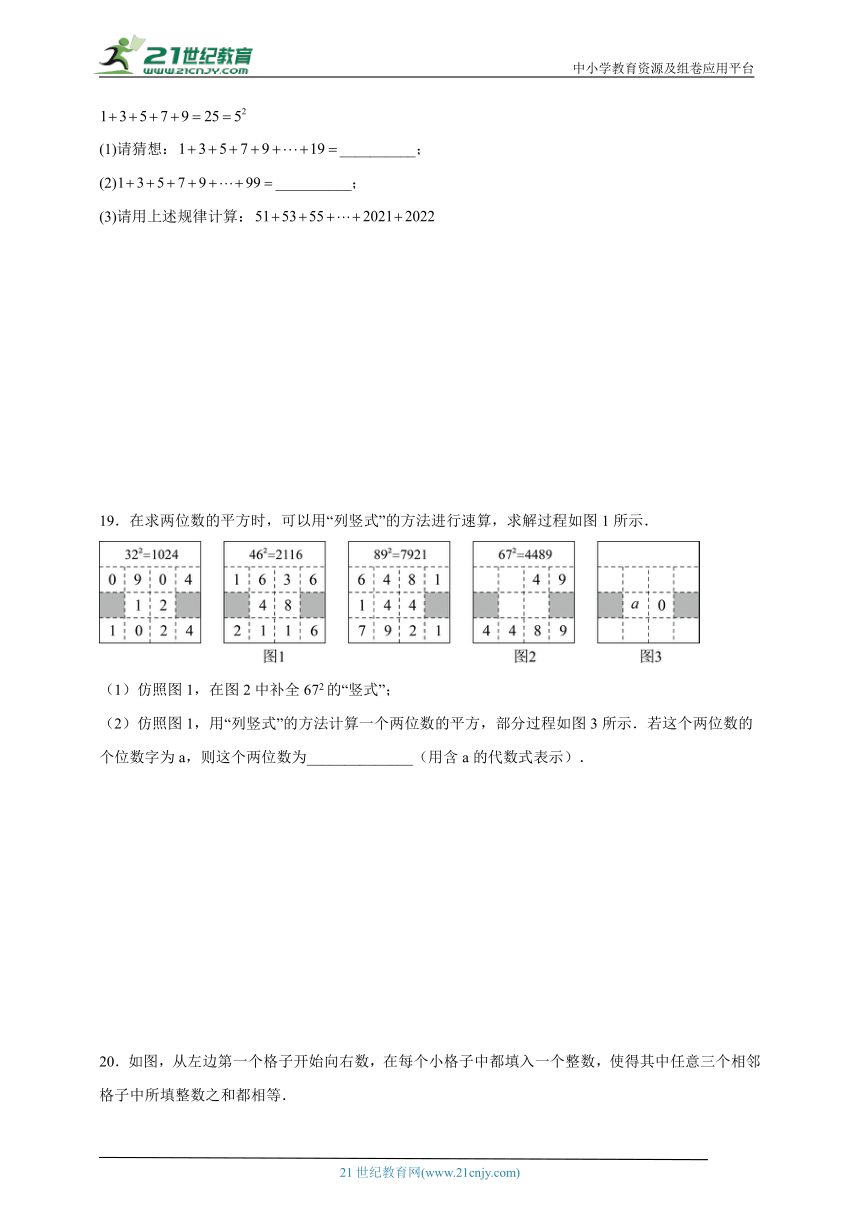
19.在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.
(1)仿照图1,在图2中补全672的“竖式”;
(2)仿照图1,用“列竖式”的方法计算一个两位数的平方,部分过程如图3所示.若这个两位数的个位数字为a,则这个两位数为______________(用含a的代数式表示).
20.如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
9 2 …
(1)可求得 ,第2017个格子中的数为 ;
(2)若前m个格子中所填整数之和为p,,则m的值为 ;当 时,;
(3)若,求的最小值.
21.如图是用大小相等的小五角星按一定规律拼成的一组图案,第个图案中有颗五角星,第个图案中有颗五角星,第个图案中有颗五角星,…,请根据你的观察完成下列问题.
(1)根据上述规律,分别写出第个图案和第个图案中小五角星的颗数;
(2)按如图所示的规律,求出第个图案中小五角星的颗数;(用含的代数式表示)
(3)第个图案中有多少颗五角星?
22.如图,用同样规格黑白两色的正方形瓷砖铺设长方形地面,观察下列图形并解答有关问题.
(1)按以上的规律依次铺下去,铺设第四个长方形地面共用多少块白瓷砖?
(2)假如铺某一块类似的长方形地面共用了72块瓷砖,那么它是第几块长方形地面?
(3)若白瓷砖每块4元,黑瓷砖每块3元,在问题(2)中购买瓷砖共需花多少元?
23.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
……
按照以上规律,解决下列问题:
(1)填空:________=10;
(2)填空:________=n(且n为正整数),并证明这个等式.
24.根据以下10个乘积,回答问题:
;;;;;
;;;;;
(1)试将以上各乘积分别写成一个平方差的形式,并写出其中一个的思考过程
(2)将以上10个乘积按照从小到大排列起来
(3)若用,,,....,表示n个乘积,其中为正数,试由(1)(2)猜测一个一般性的结论.(不要求写证明)
参考答案:
1.A
2.C
3.B
4.A
5.D
6.B
7.B
8.C
9.B
10.B
11.A
12.A
13.
14. -29 A
15.17
16. ﹣ 3
17.
18.(1)
(2)
(3)
19.(1)略;(2)a +50
20.(1);9
(2);
(3)最小值是15.
21.(1)第个图案有颗小五角星,第个图案有颗小五角星
(2)颗
(3)颗
22.(1)22
(2)六
(3)瓷砖共需花246元
23.(1)
(2)
24.(1)11×29=202-92(2)略(3)略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.3整式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.是二次三项式 B.是单项式
C.的次数是8 D.的系数是
2.如图所示:用黑白两种颜色的正五边形地砖按下图所示的规律,拼成若干个蝴蝶图案,则第7幅蝴蝶图案中白色地砖有( )
A.35块 B.27块 C.22块 D.7块
3.多项式的次数为( )
A.8 B.5 C.3 D.2
4.当时,的值为,则的值为( )
A. B.9 C.3 D.-4
5.将正整数按如图所示的规律排列下去,若有序实数对表示第排,从左到右第个数,如表示9,则表示2022的有序数对是( )
A. B. C. D.
6.下列图形都是由同样大小的五角星按照一定规律所组成的,其中第①个图形中一共有个五角星,第②个图形中一共有个五角星,第③个图形中一共有个五角星,第④个图形中一共有个五角星,,按此规律排列下去,第⑧个图形中五角星的个数为( )
A. B. C. D.
7.下列式子是单项式的是( )
A. B. C. D.
8.多项式的常数项为( )
A. B. C. D.
9.多项式3x3﹣2x2y2+x+3是( )
A.三次四项式 B.四次四项式 C.三次三项式 D.四次三项式
10.已知有一个有序数组,按下列方式重新写成数组,使得,,,,接着按同样的方式重新写成数组,使得,,,,按照这个规律继续写下去,若有一个数组满足,则n的值为( )
A.9 B.10 C.11 D.12
11.定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则: 若n=13,则第2020次“F”运算的结果是( )
A.1 B.4 C.2020 D.42020
12.如图,正方形的边长为1个单位长度,电子蚂蚁从点A出发以1个单位/秒的速度顺时针绕正方形运动,同时电子蚂蚁从点A出发以3个单位/秒的速度逆时针绕正方形运动,则第2024次相遇在( )
A.点A B.点 C.点 D.点
二、填空题
13.单项式次数是 ,系数是 .
14.将一列有理数,如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数 ,应排在A、B、C、D、E中 的位置.
……
15.如图,将第一个图(图①)所示的正三角形连接各边中点进行分割,得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,……,则得到的第五个图中,共有 个正三角形.
16.代数式﹣的系数是 ,次数为 .
17.观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球 个.
三、解答题
18.探索规律:观察下面由※组成的图案和算式,解答问题:
(1)请猜想:__________;
(2)__________;
(3)请用上述规律计算:
19.在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.
(1)仿照图1,在图2中补全672的“竖式”;
(2)仿照图1,用“列竖式”的方法计算一个两位数的平方,部分过程如图3所示.若这个两位数的个位数字为a,则这个两位数为______________(用含a的代数式表示).
20.如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
9 2 …
(1)可求得 ,第2017个格子中的数为 ;
(2)若前m个格子中所填整数之和为p,,则m的值为 ;当 时,;
(3)若,求的最小值.
21.如图是用大小相等的小五角星按一定规律拼成的一组图案,第个图案中有颗五角星,第个图案中有颗五角星,第个图案中有颗五角星,…,请根据你的观察完成下列问题.
(1)根据上述规律,分别写出第个图案和第个图案中小五角星的颗数;
(2)按如图所示的规律,求出第个图案中小五角星的颗数;(用含的代数式表示)
(3)第个图案中有多少颗五角星?
22.如图,用同样规格黑白两色的正方形瓷砖铺设长方形地面,观察下列图形并解答有关问题.
(1)按以上的规律依次铺下去,铺设第四个长方形地面共用多少块白瓷砖?
(2)假如铺某一块类似的长方形地面共用了72块瓷砖,那么它是第几块长方形地面?
(3)若白瓷砖每块4元,黑瓷砖每块3元,在问题(2)中购买瓷砖共需花多少元?
23.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
……
按照以上规律,解决下列问题:
(1)填空:________=10;
(2)填空:________=n(且n为正整数),并证明这个等式.
24.根据以下10个乘积,回答问题:
;;;;;
;;;;;
(1)试将以上各乘积分别写成一个平方差的形式,并写出其中一个的思考过程
(2)将以上10个乘积按照从小到大排列起来
(3)若用,,,....,表示n个乘积,其中为正数,试由(1)(2)猜测一个一般性的结论.(不要求写证明)
参考答案:
1.A
2.C
3.B
4.A
5.D
6.B
7.B
8.C
9.B
10.B
11.A
12.A
13.
14. -29 A
15.17
16. ﹣ 3
17.
18.(1)
(2)
(3)
19.(1)略;(2)a +50
20.(1);9
(2);
(3)最小值是15.
21.(1)第个图案有颗小五角星,第个图案有颗小五角星
(2)颗
(3)颗
22.(1)22
(2)六
(3)瓷砖共需花246元
23.(1)
(2)
24.(1)11×29=202-92(2)略(3)略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
