浙教版数学八年级上册 第一章 三角形的初步知识综合复习(无答案)
文档属性
| 名称 | 浙教版数学八年级上册 第一章 三角形的初步知识综合复习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 738.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 20:05:46 | ||
图片预览

文档简介
第一章 三角形的初步知识
班级 学号 得分 姓名
一、仔细选一选(本题有10小题,每小题3分,共30分)
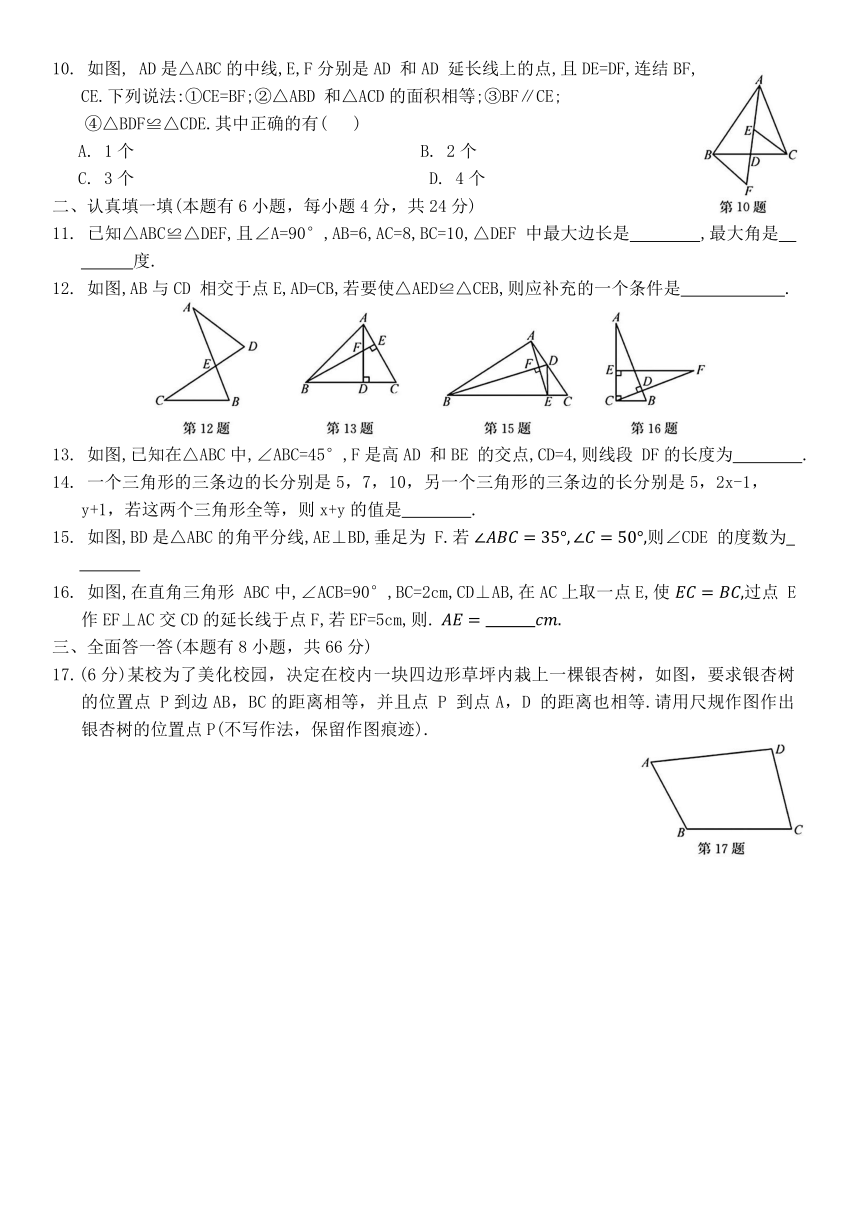
1.已知△ABC≌△DEF,∠A=80°,∠E=50°,则∠F的度数为( )
A. 30° B. 50° C. 80° D. 100°
2.如图,小强利用全等三角形的知识测量池塘两端M,N的距离,如果△PQO≌△NMO,那么需要测出长度的线段是( )
A. PO B. PQ C. MO D. MQ
3.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A. AC=BD B. ∠CAB=∠DBA C. ∠C=∠D D. BC=AD
4.如图,∠1=∠2,∠C=∠B,下列结论中不一定正确的是( )
A. △DAB≌△DAC B. △DEA≌△DFA C. CD=DE D. ∠AED=∠AFD
5.用直尺和圆规作一个角等于已知角,如图,能得出 的依据是( )
A. SAS B. AAS C. ASA D. SSS
6.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A. 0.5 B. 1 C. 1.5 D. 2
7. 如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交 AC 于点M,交AB 于点E,BC 的垂直平分线交AC于点N,交BC于点F,连结BM,BN,若AC=24,则△BMN的周长是( )
A. 36 B. 24 C. 18 D. 16
8. 如图,在Rt△ABC中,∠C=90°,以顶点 A 为圆心,适当长为半径画弧,分别交 AC,AB 于点M,N,再分别以点M,N为圆心,大于 的长为半径画弧,两弧交于点 P,作射线AP 交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A. 15 B. 30 C. 45 D. 6
9.有下列说法:① 形状相同的三角形是全等三角形;② 有两边及一角对应相等的两个三角形全等;③ 两个等边三角形一定全等;④有两角及一边对应相等的两个三角形全等.其中错误的说法有( )
A. 4个 B. 3个 C. 2个 D. 1个
10. 如图, AD是△ABC的中线,E,F分别是AD 和AD 延长线上的点,且DE=DF,连结BF,CE.下列说法:①CE=BF;②△ABD 和△ACD的面积相等;③BF∥CE;
④△BDF≌△CDE.其中正确的有( )
A. 1个 B. 2个
C. 3个 D. 4个
二、认真填一填(本题有6小题,每小题4分,共24分)
11. 已知△ABC≌△DEF,且∠A=90°,AB=6,AC=8,BC=10,△DEF 中最大边长是 ,最大角是 度.
12. 如图,AB与CD 相交于点E,AD=CB,若要使△AED≌△CEB,则应补充的一个条件是 .
13. 如图,已知在△ABC中,∠ABC=45°,F是高AD 和BE 的交点,CD=4,则线段 DF的长度为 .
14. 一个三角形的三条边的长分别是5,7,10,另一个三角形的三条边的长分别是5,2x-1, y+1,若这两个三角形全等,则x+y的值是 .
15. 如图,BD是△ABC的角平分线,AE⊥BD,垂足为 F.若 则∠CDE 的度数为
16. 如图,在直角三角形 ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使 过点 E作EF⊥AC交CD的延长线于点F,若EF=5cm,则.
三、全面答一答(本题有8小题,共66分)
17.(6分)某校为了美化校园,决定在校内一块四边形草坪内栽上一棵银杏树,如图,要求银杏树的位置点 P到边AB,BC的距离相等,并且点 P 到点A,D 的距离也相等.请用尺规作图作出银杏树的位置点P(不写作法,保留作图痕迹).
18. (6分)如图,完成下列推理过程:
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
证明:∵∠E=∠C(已知),
∠AFE=∠DFC( ),
∴∠EAF=∠2( ),
又∵∠1=∠2( ),
∴∠1=∠EAF(等量代换),
∴ +∠DAC= +∠DAC( ),
即∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE( ).
19. (6分)如图,四边形ABCD的对角线AC与BD 相交于O点,∠1=∠2,∠3=∠4.求证:BO=DO.
20. (8分)如图,点 A,F,C,D 在同一直线上,点 B 和点E 分别在直线AD 的两侧,且BC∥EF,∠A=∠D,AF=DC.求证:AB=DE.
21. (8分)如图所示,在 中,AB=AC.
(1)尺规作图:过顶点 A 作 的角平分线AD(不写作法,保留作图痕迹);
(2) 在AD 上任取一点E,连结BE,CE.求证:
22. (10分)如图,在△ABC中,AD是BC边上的中线,E是AB 边上一点,过点C作CF∥AB交ED的延长线于点 F.
(1) 求证:
(2) 当AD⊥BC,AE=1,CF=2时,求 AC的长.
23. (10分)如图,在△ABC中,∠C=90°,AC=BC,BD平分∠CBA,DE⊥AB于点E,试说明:(1) BC=BE;(2) AD+DE=BE.
24. (12分)如图,已知△ABC,按如下步骤作图:
① 分别以A,C为圆心,大于- 的长为半径画弧,两弧交于 P,Q两点;
② 作直线 PQ,分别交AB,AC于点E,D,连结CE;
③ 过C作CF∥AB交PQ于点F,连结AF.
求证:
班级 学号 得分 姓名
一、仔细选一选(本题有10小题,每小题3分,共30分)
1.已知△ABC≌△DEF,∠A=80°,∠E=50°,则∠F的度数为( )
A. 30° B. 50° C. 80° D. 100°
2.如图,小强利用全等三角形的知识测量池塘两端M,N的距离,如果△PQO≌△NMO,那么需要测出长度的线段是( )
A. PO B. PQ C. MO D. MQ
3.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
A. AC=BD B. ∠CAB=∠DBA C. ∠C=∠D D. BC=AD
4.如图,∠1=∠2,∠C=∠B,下列结论中不一定正确的是( )
A. △DAB≌△DAC B. △DEA≌△DFA C. CD=DE D. ∠AED=∠AFD
5.用直尺和圆规作一个角等于已知角,如图,能得出 的依据是( )
A. SAS B. AAS C. ASA D. SSS
6.如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A. 0.5 B. 1 C. 1.5 D. 2
7. 如图,在△ABC中,BA=BC,∠ABC=120°,AB的垂直平分线交 AC 于点M,交AB 于点E,BC 的垂直平分线交AC于点N,交BC于点F,连结BM,BN,若AC=24,则△BMN的周长是( )
A. 36 B. 24 C. 18 D. 16
8. 如图,在Rt△ABC中,∠C=90°,以顶点 A 为圆心,适当长为半径画弧,分别交 AC,AB 于点M,N,再分别以点M,N为圆心,大于 的长为半径画弧,两弧交于点 P,作射线AP 交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A. 15 B. 30 C. 45 D. 6
9.有下列说法:① 形状相同的三角形是全等三角形;② 有两边及一角对应相等的两个三角形全等;③ 两个等边三角形一定全等;④有两角及一边对应相等的两个三角形全等.其中错误的说法有( )
A. 4个 B. 3个 C. 2个 D. 1个
10. 如图, AD是△ABC的中线,E,F分别是AD 和AD 延长线上的点,且DE=DF,连结BF,CE.下列说法:①CE=BF;②△ABD 和△ACD的面积相等;③BF∥CE;
④△BDF≌△CDE.其中正确的有( )
A. 1个 B. 2个
C. 3个 D. 4个
二、认真填一填(本题有6小题,每小题4分,共24分)
11. 已知△ABC≌△DEF,且∠A=90°,AB=6,AC=8,BC=10,△DEF 中最大边长是 ,最大角是 度.
12. 如图,AB与CD 相交于点E,AD=CB,若要使△AED≌△CEB,则应补充的一个条件是 .
13. 如图,已知在△ABC中,∠ABC=45°,F是高AD 和BE 的交点,CD=4,则线段 DF的长度为 .
14. 一个三角形的三条边的长分别是5,7,10,另一个三角形的三条边的长分别是5,2x-1, y+1,若这两个三角形全等,则x+y的值是 .
15. 如图,BD是△ABC的角平分线,AE⊥BD,垂足为 F.若 则∠CDE 的度数为
16. 如图,在直角三角形 ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使 过点 E作EF⊥AC交CD的延长线于点F,若EF=5cm,则.
三、全面答一答(本题有8小题,共66分)
17.(6分)某校为了美化校园,决定在校内一块四边形草坪内栽上一棵银杏树,如图,要求银杏树的位置点 P到边AB,BC的距离相等,并且点 P 到点A,D 的距离也相等.请用尺规作图作出银杏树的位置点P(不写作法,保留作图痕迹).
18. (6分)如图,完成下列推理过程:
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
证明:∵∠E=∠C(已知),
∠AFE=∠DFC( ),
∴∠EAF=∠2( ),
又∵∠1=∠2( ),
∴∠1=∠EAF(等量代换),
∴ +∠DAC= +∠DAC( ),
即∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE( ).
19. (6分)如图,四边形ABCD的对角线AC与BD 相交于O点,∠1=∠2,∠3=∠4.求证:BO=DO.
20. (8分)如图,点 A,F,C,D 在同一直线上,点 B 和点E 分别在直线AD 的两侧,且BC∥EF,∠A=∠D,AF=DC.求证:AB=DE.
21. (8分)如图所示,在 中,AB=AC.
(1)尺规作图:过顶点 A 作 的角平分线AD(不写作法,保留作图痕迹);
(2) 在AD 上任取一点E,连结BE,CE.求证:
22. (10分)如图,在△ABC中,AD是BC边上的中线,E是AB 边上一点,过点C作CF∥AB交ED的延长线于点 F.
(1) 求证:
(2) 当AD⊥BC,AE=1,CF=2时,求 AC的长.
23. (10分)如图,在△ABC中,∠C=90°,AC=BC,BD平分∠CBA,DE⊥AB于点E,试说明:(1) BC=BE;(2) AD+DE=BE.
24. (12分)如图,已知△ABC,按如下步骤作图:
① 分别以A,C为圆心,大于- 的长为半径画弧,两弧交于 P,Q两点;
② 作直线 PQ,分别交AB,AC于点E,D,连结CE;
③ 过C作CF∥AB交PQ于点F,连结AF.
求证:
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
