浙教版数学八年级上册 第5章 一次函数 单元测试(无答案)
文档属性
| 名称 | 浙教版数学八年级上册 第5章 一次函数 单元测试(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 389.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-07 21:33:27 | ||
图片预览

文档简介
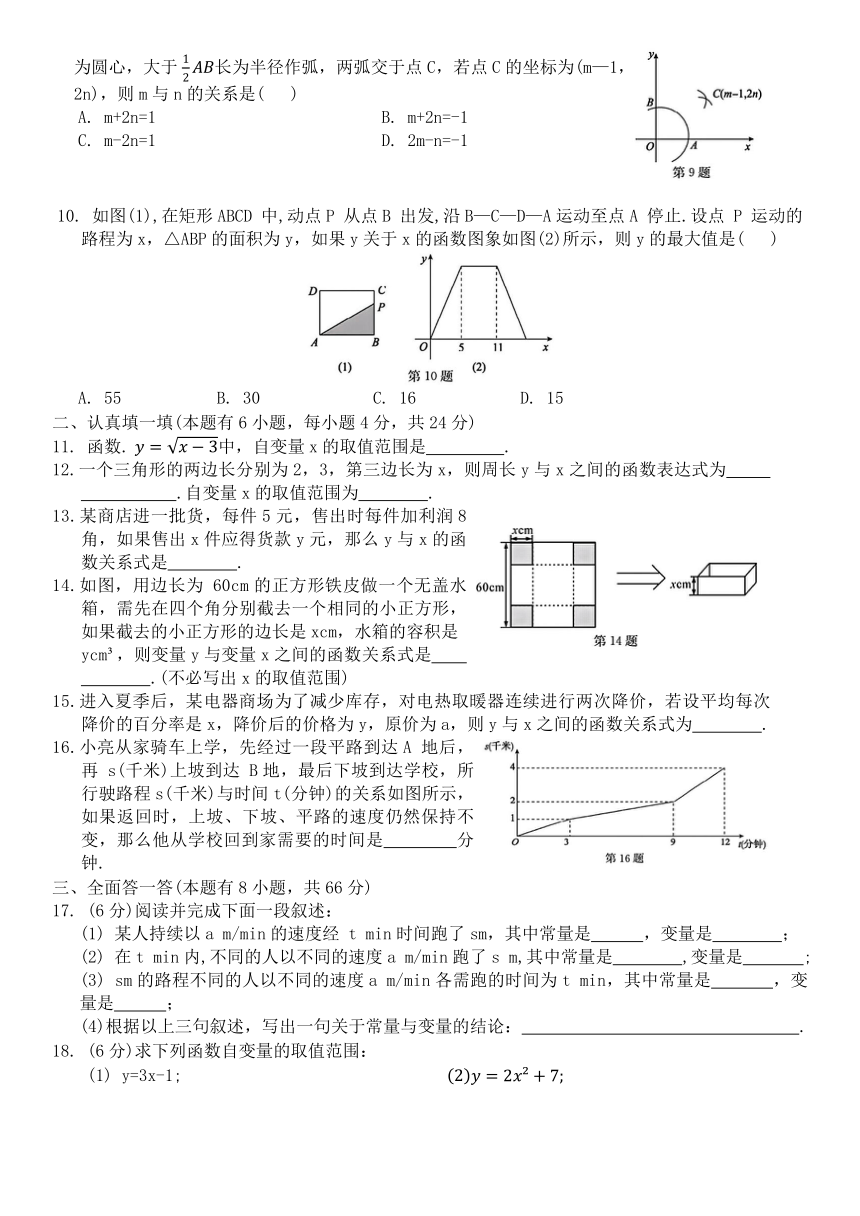
第5章 一次函数
班级 学号 得分 姓名
一、仔细选一选(本题有 10小题,每小题3分,共30分)
1.某期国债存期为三年,年利率规定为P%,不计复利,若购买x元这一期国债,三年后可得利息y元,其中 在y,P,x中,变量有( )
A. 0个 B. 1个 C. 2个 D. 3个
2.对于圆柱体侧面积公式S=2πrh,下列说法正确的是( )
A.该表达式没有常量 B. 当h越大时,S也越大
C. S,r是变量 D. S,r,h是变量
3.在函数 中,自变量x的取值范围是( )
A. x≤1 B. x≥1 C. x<1 D. x>1
4.在平整的路面上,某型号汽车紧急刹车后仍将滑行s(m),一般地,有经验公式 其中 v(km/h)表示刹车前汽车行驶的速度,当v取80时,相应的滑行距离约为( )
A. 21m B. 21km C. 30m D. 30km
5.下列曲线反映了变量y与变量x之间的关系,其中y是x的函数的是( )
6.根据如图所示的程序计算函数值.若输入的x值为 则输出的y值为( )
7.弹簧挂上物体后会伸长,现测得一弹簧的长度y(厘米)与所挂物体的质量x(千克)之间有如下关系:
物体的质量x(千克) 0 1 2 3 4 5
弹簧的长度y(厘米) 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,其中x是自变量,y是x 的函数
B.弹簧不挂重物时的长度为0厘米
C.在弹簧弹性范围内,所挂物体质量为7 千克时,弹簧的长度为13.5 厘米
D.在弹簧弹性范围内,所挂物体质量每增加1千克,弹簧的长度就增加0.5厘米
8.设等腰三角形的顶角度数为y°,底角度数为x°,则( )
A. y=180-2x(x可为全体实数) B. y=180-2x(09.如图,以点O为圆心的一段圆弧与坐标轴交于A,B两点,分别以点 A,B为圆心,大于 长为半径作弧,两弧交于点C,若点C的坐标为(m—1,2n),则m与n的关系是( )
A. m+2n=1 B. m+2n=-1
C. m-2n=1 D. 2m-n=-1
10. 如图(1),在矩形ABCD 中,动点P 从点B 出发,沿B—C—D—A运动至点A 停止.设点 P 运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图(2)所示,则y的最大值是( )
A. 55 B. 30 C. 16 D. 15
二、认真填一填(本题有6小题,每小题4分,共24分)
11. 函数. 中,自变量x的取值范围是 .
12.一个三角形的两边长分别为2,3,第三边长为x,则周长y与x之间的函数表达式为 .自变量x的取值范围为 .
13.某商店进一批货,每件5元,售出时每件加利润8角,如果售出x件应得货款y元,那么y与x的函数关系式是 .
14.如图,用边长为 60cm的正方形铁皮做一个无盖水箱,需先在四个角分别截去一个相同的小正方形,如果截去的小正方形的边长是xcm,水箱的容积是 ycm ,则变量y与变量x之间的函数关系式是 .(不必写出x的取值范围)
15.进入夏季后,某电器商场为了减少库存,对电热取暖器连续进行两次降价,若设平均每次降价的百分率是x,降价后的价格为y,原价为a,则y与x之间的函数关系式为 .
16.小亮从家骑车上学,先经过一段平路到达A 地后,再 s(千米)上坡到达 B地,最后下坡到达学校,所行驶路程s(千米)与时间t(分钟)的关系如图所示,如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是 分钟.
三、全面答一答(本题有8小题,共66分)
17. (6分)阅读并完成下面一段叙述:
(1) 某人持续以a m/min的速度经 t min时间跑了sm,其中常量是 ,变量是 ;
(2) 在t min内,不同的人以不同的速度a m/min跑了s m,其中常量是 ,变量是 ;
(3) sm的路程不同的人以不同的速度a m/min各需跑的时间为t min,其中常量是 ,变量是 ;
(4)根据以上三句叙述,写出一句关于常量与变量的结论: .
18. (6分)求下列函数自变量的取值范围:
(1) y=3x-1;
19.(6分)如图,每个图形都是由若干颗棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)颗棋子,设每个图案的棋子总数为 S.
图中棋子的排列有什么规律 请写出S关于n的函数关系式,并写出自变量的取值范围.
20.(8分)心理学家发现,学生对概念的接受能力 y与提出概念所用的时间x(min)之间有如下关系(其中( x≤20):
提出概念所用的时间(x,单位: min) 2 5 7 10 12 13 14 17 20
对概念的接受能力(y) 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)当提出概念所用的时间是10min时,学生的接受能力是多少
(2)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强
(3)从表中可知,当时间x在什么范围内,学生的接受能力逐步增强 当时间x在什么范围内,学生的接受能力逐步降低
21. (8分)如图,长方形ABCD 中, . 点 P 在AB 上运动,设 图中阴影部分的面积为y.
(1)写出阴影部分的面积y与x之间的函数表达式和自变量x的取值范围;
(2)点 P 在什么位置时,阴影部分的面积等于 20
22. (10分)将一些长为30cm,宽为10cm的长方形白纸,按如图所示的方法黏合起来,黏合部分的宽为2cm.
(1)求5张白纸黏合后的长度;
(2)设x张白纸黏合后的纸条总长度为ycm,写出y关于x的函数关系式;
(3) 当x=20张时,y的值是多少
23.(10分)张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿,返回途中在读报栏前看了一会儿报,下图是据此情景画出的图象,s(m)表示张爷爷离开家的距离,t(min)表示外出散步的时间.请你回答下面的问题:
(1)张爷爷在什么地方碰到老邻居的 交谈了多长时间
(2)读报栏大约离家多少路程
(3)图中反映了哪些变量之间的关系 其中哪个是自变量 你能将其中某个变量看成另一个变量的函数吗
24.(12分)为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c 元收费,该市某户今年9,10月份的用水量和所交水费如下表所示:
月份 用水量(立方米) 收费(元)
9 5 7.5
10 9 27
设某户每月用水量为x(立方米),应交水费为y(元).
(1) 求a,c的值;
(2) 当x≤6,x>6时,分别写出y与x的函数关系式;
(2)若该户11月份用水量为8立方米,求该户11月份水费是多少元
班级 学号 得分 姓名
一、仔细选一选(本题有 10小题,每小题3分,共30分)
1.某期国债存期为三年,年利率规定为P%,不计复利,若购买x元这一期国债,三年后可得利息y元,其中 在y,P,x中,变量有( )
A. 0个 B. 1个 C. 2个 D. 3个
2.对于圆柱体侧面积公式S=2πrh,下列说法正确的是( )
A.该表达式没有常量 B. 当h越大时,S也越大
C. S,r是变量 D. S,r,h是变量
3.在函数 中,自变量x的取值范围是( )
A. x≤1 B. x≥1 C. x<1 D. x>1
4.在平整的路面上,某型号汽车紧急刹车后仍将滑行s(m),一般地,有经验公式 其中 v(km/h)表示刹车前汽车行驶的速度,当v取80时,相应的滑行距离约为( )
A. 21m B. 21km C. 30m D. 30km
5.下列曲线反映了变量y与变量x之间的关系,其中y是x的函数的是( )
6.根据如图所示的程序计算函数值.若输入的x值为 则输出的y值为( )
7.弹簧挂上物体后会伸长,现测得一弹簧的长度y(厘米)与所挂物体的质量x(千克)之间有如下关系:
物体的质量x(千克) 0 1 2 3 4 5
弹簧的长度y(厘米) 10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.x与y都是变量,其中x是自变量,y是x 的函数
B.弹簧不挂重物时的长度为0厘米
C.在弹簧弹性范围内,所挂物体质量为7 千克时,弹簧的长度为13.5 厘米
D.在弹簧弹性范围内,所挂物体质量每增加1千克,弹簧的长度就增加0.5厘米
8.设等腰三角形的顶角度数为y°,底角度数为x°,则( )
A. y=180-2x(x可为全体实数) B. y=180-2x(0
A. m+2n=1 B. m+2n=-1
C. m-2n=1 D. 2m-n=-1
10. 如图(1),在矩形ABCD 中,动点P 从点B 出发,沿B—C—D—A运动至点A 停止.设点 P 运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图(2)所示,则y的最大值是( )
A. 55 B. 30 C. 16 D. 15
二、认真填一填(本题有6小题,每小题4分,共24分)
11. 函数. 中,自变量x的取值范围是 .
12.一个三角形的两边长分别为2,3,第三边长为x,则周长y与x之间的函数表达式为 .自变量x的取值范围为 .
13.某商店进一批货,每件5元,售出时每件加利润8角,如果售出x件应得货款y元,那么y与x的函数关系式是 .
14.如图,用边长为 60cm的正方形铁皮做一个无盖水箱,需先在四个角分别截去一个相同的小正方形,如果截去的小正方形的边长是xcm,水箱的容积是 ycm ,则变量y与变量x之间的函数关系式是 .(不必写出x的取值范围)
15.进入夏季后,某电器商场为了减少库存,对电热取暖器连续进行两次降价,若设平均每次降价的百分率是x,降价后的价格为y,原价为a,则y与x之间的函数关系式为 .
16.小亮从家骑车上学,先经过一段平路到达A 地后,再 s(千米)上坡到达 B地,最后下坡到达学校,所行驶路程s(千米)与时间t(分钟)的关系如图所示,如果返回时,上坡、下坡、平路的速度仍然保持不变,那么他从学校回到家需要的时间是 分钟.
三、全面答一答(本题有8小题,共66分)
17. (6分)阅读并完成下面一段叙述:
(1) 某人持续以a m/min的速度经 t min时间跑了sm,其中常量是 ,变量是 ;
(2) 在t min内,不同的人以不同的速度a m/min跑了s m,其中常量是 ,变量是 ;
(3) sm的路程不同的人以不同的速度a m/min各需跑的时间为t min,其中常量是 ,变量是 ;
(4)根据以上三句叙述,写出一句关于常量与变量的结论: .
18. (6分)求下列函数自变量的取值范围:
(1) y=3x-1;
19.(6分)如图,每个图形都是由若干颗棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)颗棋子,设每个图案的棋子总数为 S.
图中棋子的排列有什么规律 请写出S关于n的函数关系式,并写出自变量的取值范围.
20.(8分)心理学家发现,学生对概念的接受能力 y与提出概念所用的时间x(min)之间有如下关系(其中( x≤20):
提出概念所用的时间(x,单位: min) 2 5 7 10 12 13 14 17 20
对概念的接受能力(y) 47.8 53.5 56.3 59 59.8 59.9 59.8 58.3 55
(1)当提出概念所用的时间是10min时,学生的接受能力是多少
(2)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强
(3)从表中可知,当时间x在什么范围内,学生的接受能力逐步增强 当时间x在什么范围内,学生的接受能力逐步降低
21. (8分)如图,长方形ABCD 中, . 点 P 在AB 上运动,设 图中阴影部分的面积为y.
(1)写出阴影部分的面积y与x之间的函数表达式和自变量x的取值范围;
(2)点 P 在什么位置时,阴影部分的面积等于 20
22. (10分)将一些长为30cm,宽为10cm的长方形白纸,按如图所示的方法黏合起来,黏合部分的宽为2cm.
(1)求5张白纸黏合后的长度;
(2)设x张白纸黏合后的纸条总长度为ycm,写出y关于x的函数关系式;
(3) 当x=20张时,y的值是多少
23.(10分)张爷爷晚饭以后外出散步,碰到老邻居,交谈了一会儿,返回途中在读报栏前看了一会儿报,下图是据此情景画出的图象,s(m)表示张爷爷离开家的距离,t(min)表示外出散步的时间.请你回答下面的问题:
(1)张爷爷在什么地方碰到老邻居的 交谈了多长时间
(2)读报栏大约离家多少路程
(3)图中反映了哪些变量之间的关系 其中哪个是自变量 你能将其中某个变量看成另一个变量的函数吗
24.(12分)为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c 元收费,该市某户今年9,10月份的用水量和所交水费如下表所示:
月份 用水量(立方米) 收费(元)
9 5 7.5
10 9 27
设某户每月用水量为x(立方米),应交水费为y(元).
(1) 求a,c的值;
(2) 当x≤6,x>6时,分别写出y与x的函数关系式;
(2)若该户11月份用水量为8立方米,求该户11月份水费是多少元
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
