浙教版数学八年级下册 第五章 特殊平行四边形综合测试卷 (含答案)
文档属性
| 名称 | 浙教版数学八年级下册 第五章 特殊平行四边形综合测试卷 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 938.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-09 08:17:12 | ||
图片预览


文档简介
第五章综合测试卷 特殊平行四边形
班级 学号 得分 姓名
一、仔细选一选(本大题有10小题,每小题3分,共30分)
1.下面性质中,菱形具有而矩形不具有的是( )
A. 邻角互补 B. 内角和为360° C. 对角线相等 D. 对角线互相垂直
2.如图,在△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A. AB=AC B. AD=BD C. BE⊥AC D. BE平分∠ABC
3.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH等于( )
A B C. 5 D. 4
4.若矩形的一条对角线与一边的夹角是40°,则两条对角线所夹的锐角的度数为( )
A. 80° B. 60° C. 45° D. 40°
5. 如图,在边长为2的正方形 ABCD中,M为边AD 的中点,延长MD 至点E,使ME=MC,以 DE 为边作正方形DEFG,点G在边CD上,则DG的长为( )
6. 如图,矩形ABCD的周长是28,点O是线段AC的中点,点 P是AD 的中点,△AOD 的周长与△COD 的周长差是2(且AD>CD),则△AOP的周长为( )
A. 12 B. 14 C. 16 D. 18
7. 如图,边长为m+3的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠且无缝隙),若拼成的矩形一边长为3,则另一边长是( )
A. 2m+3 B. 2m+6 C. m+3 D. m+6
8. 如图,在矩形纸片 ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点 B落在点E 处,CE交AD 于点F,则DF的长等于( )
A C. 7/3
9. 如图,AC,BD 是菱形ABCD 的对角线,交于点O,E,F分别是边AB,AD 的中点,连结 EF,EO,FO,则下列结论错误的是( )
A. EF=DO B. EF⊥AO
C. 四边形 EOFA 是菱形 D. 四边形 EBOF 是菱形
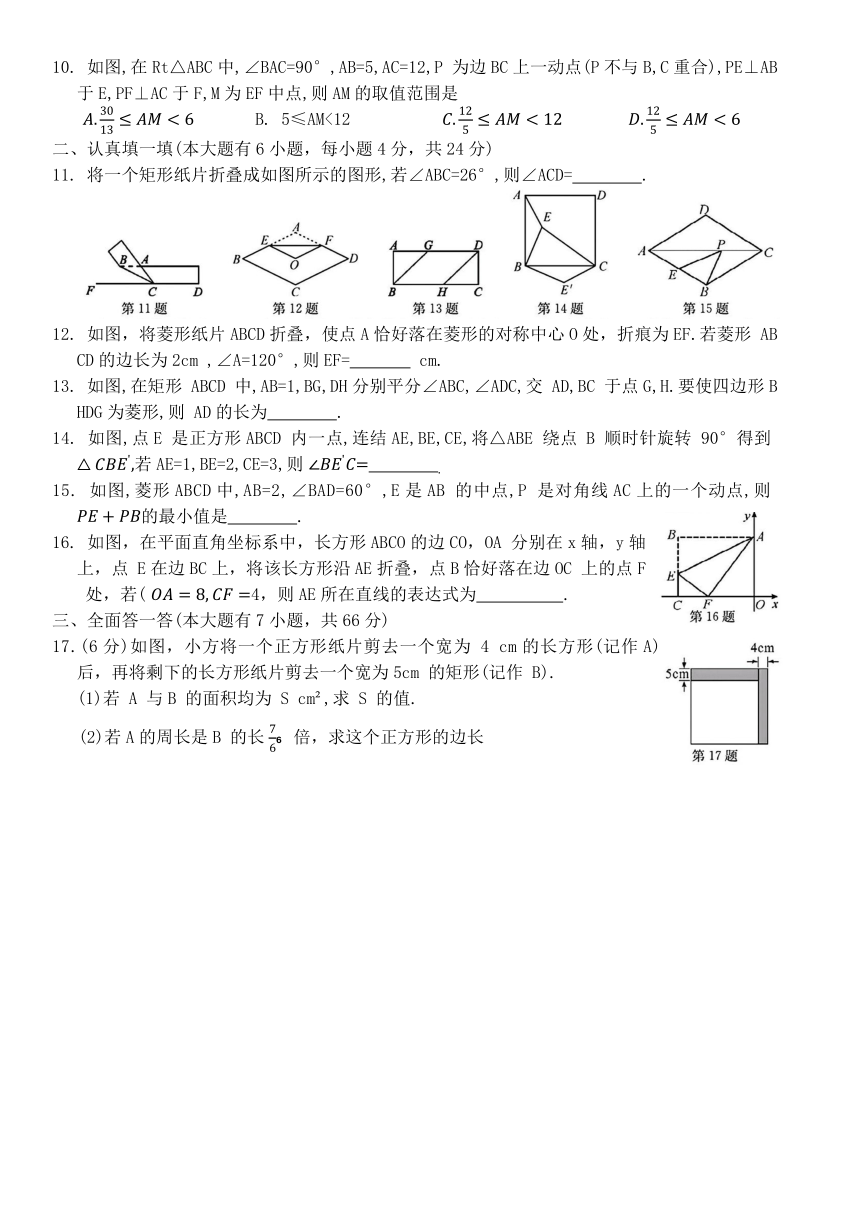
10. 如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P 为边BC上一动点(P不与B,C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是
B. 5≤AM<12
二、认真填一填(本大题有6小题,每小题4分,共24分)
11. 将一个矩形纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD= .
12. 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形 ABCD的边长为2cm ,∠A=120°,则EF= cm.
13. 如图,在矩形 ABCD 中,AB=1,BG,DH分别平分∠ABC,∠ADC,交 AD,BC 于点G,H.要使四边形BHDG为菱形,则 AD的长为 .
14. 如图,点E 是正方形ABCD 内一点,连结AE,BE,CE,将△ABE 绕点 B 顺时针旋转 90°得到 若AE=1,BE=2,CE=3,则
15. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB 的中点,P 是对角线AC上的一个动点,则 的最小值是 .
16. 如图,在平面直角坐标系中,长方形ABCO的边CO,OA 分别在x轴,y轴上,点 E在边BC上,将该长方形沿AE折叠,点B恰好落在边OC 上的点F 处,若( 4,则AE所在直线的表达式为 .
三、全面答一答(本大题有7小题,共66分)
17.(6分)如图,小方将一个正方形纸片剪去一个宽为 4 cm的长方形(记作A)后,再将剩下的长方形纸片剪去一个宽为5cm 的矩形(记作 B).
(1)若 A 与B 的面积均为 S cm ,求 S 的值.
(2)若A的周长是B 的长 倍,求这个正方形的边长
18.(8分)如图,已知在菱形 ABCD中,点 E,O,F 分别是边AB,AC,AD 的中点,连结CE,CF,OE,OF.
(1)求证:
(2)当AB与BC满足什么条件时,四边形AEOF为正方形 请说明理由.
19.(8分)如图,AC为矩形ABCD 的对角线,将边AB沿AE折叠,使点 B 落在AC上的点M处,将边CD沿CF 折叠,使点 D落在AC 上的点 N 处.
(1)求证:四边形AECF是平行四边形.
(2)若 ,求四边形 AECF的面积.
20.(10分)如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合), 于点 E, 于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由.
(2)若正方形 ABCD 的边长为1,. ,求线段 BG的长.
21.(10分)如图,在 中, ,垂足分别为E,F,且BE=DF.
(1)求证: 是菱形.
(2)若 求的面积.
22. (12分)如图,在Rt△ABC中,. ,过点 C的直线MN∥AB,D为AB 边上一点,过点 D作DE⊥BC,交直线MN于E,垂足为 F,连结CD,BE.
(1)求证:
(2)当D为AB 中点时,四边形 BECD 是什么特殊四边形 说明理由.
(3)若D为AB 中点,则当∠A= 度时,四边形 BECD 是正方形.
23. (12分)
(1) 如图①,在锐角. 中,分别以AB,AC为边向外作等边三角形ABE 和等边三角形ACD,连结BD,CE,试猜想 BD 与CE 的大小关系,并说明理由.
【深入探究】
(2)如图②,在△ABC中, ,分别以AB,AC为边向外作正方形ABNE和正方形ACMD,连结BD,求 BD的长.
(3)如图③,在(2)的条件下,以AC 为直角边在线段AC 的左侧作等腰直角三角形ACD,求BD的长.
第五章综合测试卷 特殊平行四边形
1. D 2. D 3. A 4. A 5. D 6. A 7. A 8. B
9. D 解析:在菱形ABCD 中,BO=OD,BD⊥AC,∵E,F分别是边AB,AD的中点,∴2EF=BD=BO+OD,EF∥BD,∴EF=DO,EF⊥AO,∵E是AB的中点,O是BD 的中点,∴2EO=AD,同理可得:2FO=AB,∵AB=AD,∴AE=OE=OF=AF,∴四边形 EOFA 是菱形,∵AB≠BD,BE≠BO,∴四边形 EBOF 是平行四边形,不是菱形,故选:D.
10. A 解析:在Rt△ABC中,∵∠BAC=90°,AB=5,AC=12, B 于 E,PF⊥AC 于 F,∴∠PEA=∠PFA=∠EAF=90°,∴四边形AEPF是矩形,∵M是EF 的中点,∴延长AM经过点P,. 当PA⊥CB时,PA最小,此时 . AM的最小值为 6,故选 A.
11.128° 12
解析:∵在矩形ABCD中,BG平分∠ABC,∴∠A=90°,∠ABG=45°,∴∠AGB=∠ABG=45°,∴AB=AG.又∵AB 又∵四边形BHDG 为菱形,
14.135° 15
17.解:(1)设正方形的边长为 xcm,由题意得:4x=5(x-4),解得x=20,∴S=4x=4×20=80,|即S的值为 80.(2)设正方形的边长为y cm,6(2y+8)=7×2[5=(y-4) ]解得y=17.即正方形的边长为17 cm.
18.(1)证明:∵四边形 ABCD 为菱形,∴AB=BC=CD=DA,∠B=∠D,又E,F分别是AB,AD中点,∴BE=DF,∴△CBE≌△CDF(SAS).
2)解:当AB⊥BC,则四边形AEOF为正方形.理由如下,∵E,O分别是AB,AC中点,∴EO∥BC,又BC∥AD,∴OE∥AD,即OE∥AF,同理可证OF∥AE,所以四边形AEOF 为平行四边形.由1)可得AE=AF,所以平行四边形 AEOF 为菱形.因为 BC⊥\B,所以∠BAD=90°,所以菱形AEOF 为正方形.
19.(1)证明:由题意知,AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°,∴∠ANF=90°,∠CME=90°.∵四边形BCD为矩形,∴AB=CD,AD∥BC,∴AM=CN,∴AM-MN= CN - MN, 即 在 和 中, ∴△ANF≌△CME,∴AF=CE.又∵AF∥
CE,∴四边形AECF 是平行四边形.
(2)解:∵AB=6,AC=10.∴BC=8,设CE=x,则 在Rt△CEM中,
解得x=5,∴四边形AECF的面积为:EC·AB=5×6=30.
20.解:(1)结论: 理由:连结CG.∵四边形 AB-CD是正方形,∴A,C关于对角线BD 对称,∵点 G 在 BD 上,∴GA=GC,∵GE⊥DC 于点E,GF⊥BC于点F,∴∠GEC= .四边形 EGFC是矩形,∴CF=GE,在Rt△GFC中,
(2)过点A作AH⊥BG,垂足为炔对婴边形ABCD 是正方形,∴∠ABD=∠GBF=45°,∵GF快对快对快对。∠BGF=45°,∵∠AGF=105°, , 在 Rt△ABH 中, 在 Rt△AGH 中,
21.(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D,∵AE1 ≌△AFD,∴AB=AD,∴平行四边形ABCD是菱形.(2)解:连结BD交AC于点O.∵四边形ABCD是菱形,AC=6,∴AC⊥BD, AC×BD=24.
22.(1)证明:∵DE⊥BC,∴∠DFB=90°,∵∠ACB=90°,∴∠DFB=∠ACB,∴DE∥AC,∵MN∥AB,∴四边形ADEC为平行四边形,∴CE=AD.
(2)解:菱形,理由如下:在直角三角形ABC中,∵D为AB中点,∴BD=AD,∵CE=AD,∴BD=CE,
∴MN∥AB,∴四边形BECD是平行四边形,∵∠ACB=90°,D 是AB 中点,∴BD=CD,∴四边形BECD 是菱形.(3)若 D为AB 中点,则当. 时,四边形 BECD是正方形,理由:∵∠A=45°,∠ACB=90°, ∴∠ABC=45°,∵四边形 BECD是菱形,∴DC=DB,∴∠DBC=∠DCB=45°,∴∠CDB=90°,∵四边形BECD是菱形,∴四边形BECD 是正方形,故答案为45.
23.(1)解:BD=CE.理由:∵△ABE和△ACD都是等边三角形,∴∠BAE=∠CAD=60°,AE=AB,AC=AD,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD(SAS),∴BD=CE.
(2)如图②,连结 EC,EB.在正方形 ABNE 和正方形ACMD 中,∵AC=AD,AE=AB,∠BAE=∠CAD=90°,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD(SAS),∴BD=CE.∵AE=AB=5,∴BE= ,∠ABE∠AEB=45°.又∵∠ABC=45°,∴∠ABC+∠ABE=45°+45°= 答:BD长是
(3)如图③,在线段AC的右侧过点A 作AE⊥AB于点A,交 BC的延长线于点E,∴∠BAE=90°.又∵∠ABC=45°,∴∠E=∠ABC=45°,∴AE=AB=5,BE +5 = .又∵∠AC=∠ADC=45°,∴∠BAE=∠DAC=90°,∴∠BAE-∠BAC=∠DAC--∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD(SAS),∴BD=CE.∵BC=3,∴BD=CE=( --3)( cm)答:BD长是
班级 学号 得分 姓名
一、仔细选一选(本大题有10小题,每小题3分,共30分)
1.下面性质中,菱形具有而矩形不具有的是( )
A. 邻角互补 B. 内角和为360° C. 对角线相等 D. 对角线互相垂直
2.如图,在△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A. AB=AC B. AD=BD C. BE⊥AC D. BE平分∠ABC
3.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH等于( )
A B C. 5 D. 4
4.若矩形的一条对角线与一边的夹角是40°,则两条对角线所夹的锐角的度数为( )
A. 80° B. 60° C. 45° D. 40°
5. 如图,在边长为2的正方形 ABCD中,M为边AD 的中点,延长MD 至点E,使ME=MC,以 DE 为边作正方形DEFG,点G在边CD上,则DG的长为( )
6. 如图,矩形ABCD的周长是28,点O是线段AC的中点,点 P是AD 的中点,△AOD 的周长与△COD 的周长差是2(且AD>CD),则△AOP的周长为( )
A. 12 B. 14 C. 16 D. 18
7. 如图,边长为m+3的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠且无缝隙),若拼成的矩形一边长为3,则另一边长是( )
A. 2m+3 B. 2m+6 C. m+3 D. m+6
8. 如图,在矩形纸片 ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点 B落在点E 处,CE交AD 于点F,则DF的长等于( )
A C. 7/3
9. 如图,AC,BD 是菱形ABCD 的对角线,交于点O,E,F分别是边AB,AD 的中点,连结 EF,EO,FO,则下列结论错误的是( )
A. EF=DO B. EF⊥AO
C. 四边形 EOFA 是菱形 D. 四边形 EBOF 是菱形
10. 如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,P 为边BC上一动点(P不与B,C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是
B. 5≤AM<12
二、认真填一填(本大题有6小题,每小题4分,共24分)
11. 将一个矩形纸片折叠成如图所示的图形,若∠ABC=26°,则∠ACD= .
12. 如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形 ABCD的边长为2cm ,∠A=120°,则EF= cm.
13. 如图,在矩形 ABCD 中,AB=1,BG,DH分别平分∠ABC,∠ADC,交 AD,BC 于点G,H.要使四边形BHDG为菱形,则 AD的长为 .
14. 如图,点E 是正方形ABCD 内一点,连结AE,BE,CE,将△ABE 绕点 B 顺时针旋转 90°得到 若AE=1,BE=2,CE=3,则
15. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB 的中点,P 是对角线AC上的一个动点,则 的最小值是 .
16. 如图,在平面直角坐标系中,长方形ABCO的边CO,OA 分别在x轴,y轴上,点 E在边BC上,将该长方形沿AE折叠,点B恰好落在边OC 上的点F 处,若( 4,则AE所在直线的表达式为 .
三、全面答一答(本大题有7小题,共66分)
17.(6分)如图,小方将一个正方形纸片剪去一个宽为 4 cm的长方形(记作A)后,再将剩下的长方形纸片剪去一个宽为5cm 的矩形(记作 B).
(1)若 A 与B 的面积均为 S cm ,求 S 的值.
(2)若A的周长是B 的长 倍,求这个正方形的边长
18.(8分)如图,已知在菱形 ABCD中,点 E,O,F 分别是边AB,AC,AD 的中点,连结CE,CF,OE,OF.
(1)求证:
(2)当AB与BC满足什么条件时,四边形AEOF为正方形 请说明理由.
19.(8分)如图,AC为矩形ABCD 的对角线,将边AB沿AE折叠,使点 B 落在AC上的点M处,将边CD沿CF 折叠,使点 D落在AC 上的点 N 处.
(1)求证:四边形AECF是平行四边形.
(2)若 ,求四边形 AECF的面积.
20.(10分)如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合), 于点 E, 于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由.
(2)若正方形 ABCD 的边长为1,. ,求线段 BG的长.
21.(10分)如图,在 中, ,垂足分别为E,F,且BE=DF.
(1)求证: 是菱形.
(2)若 求的面积.
22. (12分)如图,在Rt△ABC中,. ,过点 C的直线MN∥AB,D为AB 边上一点,过点 D作DE⊥BC,交直线MN于E,垂足为 F,连结CD,BE.
(1)求证:
(2)当D为AB 中点时,四边形 BECD 是什么特殊四边形 说明理由.
(3)若D为AB 中点,则当∠A= 度时,四边形 BECD 是正方形.
23. (12分)
(1) 如图①,在锐角. 中,分别以AB,AC为边向外作等边三角形ABE 和等边三角形ACD,连结BD,CE,试猜想 BD 与CE 的大小关系,并说明理由.
【深入探究】
(2)如图②,在△ABC中, ,分别以AB,AC为边向外作正方形ABNE和正方形ACMD,连结BD,求 BD的长.
(3)如图③,在(2)的条件下,以AC 为直角边在线段AC 的左侧作等腰直角三角形ACD,求BD的长.
第五章综合测试卷 特殊平行四边形
1. D 2. D 3. A 4. A 5. D 6. A 7. A 8. B
9. D 解析:在菱形ABCD 中,BO=OD,BD⊥AC,∵E,F分别是边AB,AD的中点,∴2EF=BD=BO+OD,EF∥BD,∴EF=DO,EF⊥AO,∵E是AB的中点,O是BD 的中点,∴2EO=AD,同理可得:2FO=AB,∵AB=AD,∴AE=OE=OF=AF,∴四边形 EOFA 是菱形,∵AB≠BD,BE≠BO,∴四边形 EBOF 是平行四边形,不是菱形,故选:D.
10. A 解析:在Rt△ABC中,∵∠BAC=90°,AB=5,AC=12, B 于 E,PF⊥AC 于 F,∴∠PEA=∠PFA=∠EAF=90°,∴四边形AEPF是矩形,∵M是EF 的中点,∴延长AM经过点P,. 当PA⊥CB时,PA最小,此时 . AM的最小值为 6,故选 A.
11.128° 12
解析:∵在矩形ABCD中,BG平分∠ABC,∴∠A=90°,∠ABG=45°,∴∠AGB=∠ABG=45°,∴AB=AG.又∵AB 又∵四边形BHDG 为菱形,
14.135° 15
17.解:(1)设正方形的边长为 xcm,由题意得:4x=5(x-4),解得x=20,∴S=4x=4×20=80,|即S的值为 80.(2)设正方形的边长为y cm,6(2y+8)=7×2[5=(y-4) ]解得y=17.即正方形的边长为17 cm.
18.(1)证明:∵四边形 ABCD 为菱形,∴AB=BC=CD=DA,∠B=∠D,又E,F分别是AB,AD中点,∴BE=DF,∴△CBE≌△CDF(SAS).
2)解:当AB⊥BC,则四边形AEOF为正方形.理由如下,∵E,O分别是AB,AC中点,∴EO∥BC,又BC∥AD,∴OE∥AD,即OE∥AF,同理可证OF∥AE,所以四边形AEOF 为平行四边形.由1)可得AE=AF,所以平行四边形 AEOF 为菱形.因为 BC⊥\B,所以∠BAD=90°,所以菱形AEOF 为正方形.
19.(1)证明:由题意知,AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°,∴∠ANF=90°,∠CME=90°.∵四边形BCD为矩形,∴AB=CD,AD∥BC,∴AM=CN,∴AM-MN= CN - MN, 即 在 和 中, ∴△ANF≌△CME,∴AF=CE.又∵AF∥
CE,∴四边形AECF 是平行四边形.
(2)解:∵AB=6,AC=10.∴BC=8,设CE=x,则 在Rt△CEM中,
解得x=5,∴四边形AECF的面积为:EC·AB=5×6=30.
20.解:(1)结论: 理由:连结CG.∵四边形 AB-CD是正方形,∴A,C关于对角线BD 对称,∵点 G 在 BD 上,∴GA=GC,∵GE⊥DC 于点E,GF⊥BC于点F,∴∠GEC= .四边形 EGFC是矩形,∴CF=GE,在Rt△GFC中,
(2)过点A作AH⊥BG,垂足为炔对婴边形ABCD 是正方形,∴∠ABD=∠GBF=45°,∵GF快对快对快对。∠BGF=45°,∵∠AGF=105°, , 在 Rt△ABH 中, 在 Rt△AGH 中,
21.(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D,∵AE1 ≌△AFD,∴AB=AD,∴平行四边形ABCD是菱形.(2)解:连结BD交AC于点O.∵四边形ABCD是菱形,AC=6,∴AC⊥BD, AC×BD=24.
22.(1)证明:∵DE⊥BC,∴∠DFB=90°,∵∠ACB=90°,∴∠DFB=∠ACB,∴DE∥AC,∵MN∥AB,∴四边形ADEC为平行四边形,∴CE=AD.
(2)解:菱形,理由如下:在直角三角形ABC中,∵D为AB中点,∴BD=AD,∵CE=AD,∴BD=CE,
∴MN∥AB,∴四边形BECD是平行四边形,∵∠ACB=90°,D 是AB 中点,∴BD=CD,∴四边形BECD 是菱形.(3)若 D为AB 中点,则当. 时,四边形 BECD是正方形,理由:∵∠A=45°,∠ACB=90°, ∴∠ABC=45°,∵四边形 BECD是菱形,∴DC=DB,∴∠DBC=∠DCB=45°,∴∠CDB=90°,∵四边形BECD是菱形,∴四边形BECD 是正方形,故答案为45.
23.(1)解:BD=CE.理由:∵△ABE和△ACD都是等边三角形,∴∠BAE=∠CAD=60°,AE=AB,AC=AD,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD(SAS),∴BD=CE.
(2)如图②,连结 EC,EB.在正方形 ABNE 和正方形ACMD 中,∵AC=AD,AE=AB,∠BAE=∠CAD=90°,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD(SAS),∴BD=CE.∵AE=AB=5,∴BE= ,∠ABE∠AEB=45°.又∵∠ABC=45°,∴∠ABC+∠ABE=45°+45°= 答:BD长是
(3)如图③,在线段AC的右侧过点A 作AE⊥AB于点A,交 BC的延长线于点E,∴∠BAE=90°.又∵∠ABC=45°,∴∠E=∠ABC=45°,∴AE=AB=5,BE +5 = .又∵∠AC=∠ADC=45°,∴∠BAE=∠DAC=90°,∴∠BAE-∠BAC=∠DAC--∠BAC,即∠EAC=∠BAD,∴△EAC≌△BAD(SAS),∴BD=CE.∵BC=3,∴BD=CE=( --3)( cm)答:BD长是
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
