【专题精练】浙教七年级上册 一元一次方程应用行程问题(含详细解析)
文档属性
| 名称 | 【专题精练】浙教七年级上册 一元一次方程应用行程问题(含详细解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-12 15:28:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版七年级上册数学 一元一次方程应用行程问题 专题训练
1.某景区门票上绘制了简易游览图(如图),从游客中心到观景台有山路,从观景台到山顶有山路,圆圆同学从导游口中得知:离观景台处有一个凉亭,离凉亭处有一个小卖部.
(1)圆圆同学把这张图中的游览线路抽象成一条数轴,其中游客中心是原点,往山顶方向为正方向,为1个单位长度,请在数轴上标出小卖部所有可能的位置,并用数字表示出来.
(2)圆圆同学上山时从游客中心到山顶共用了小时,下山时从山顶到游客中心的平均速度为千米/小时,求圆圆同学上山、下山全程的平均速度(用含和的代数式表示).
(3)若凉亭在观景台到山顶的途中,方方同学上午从游客中心出发匀速上山,于到达观景台,在观景台停留30分钟后,以同样的速度继续上山,途中又在凉亭休息了15分钟,到山顶游玩了35分钟后下山(下山途中不再停留),为了在下午准时回到游客中心,方方同学下山的速度比上山的速度快,求的值.
2.如图,城乡公交车行驶在笔直的公路上,这条路上有A,B,C三个站点,已知相邻两站之间的距离分别为千米,千米,且每个站点的停靠时间为4分钟.已知甲、乙两车于上午8:00分别从A站,C站出发相向而行,两车的速度均为30千米/小时,设两车出发t小时后,问:
(1)甲、乙两车到达B站分别用时多少?
(2)求两车相遇的时刻.
(3)当两车相距4千米时,求t的值.
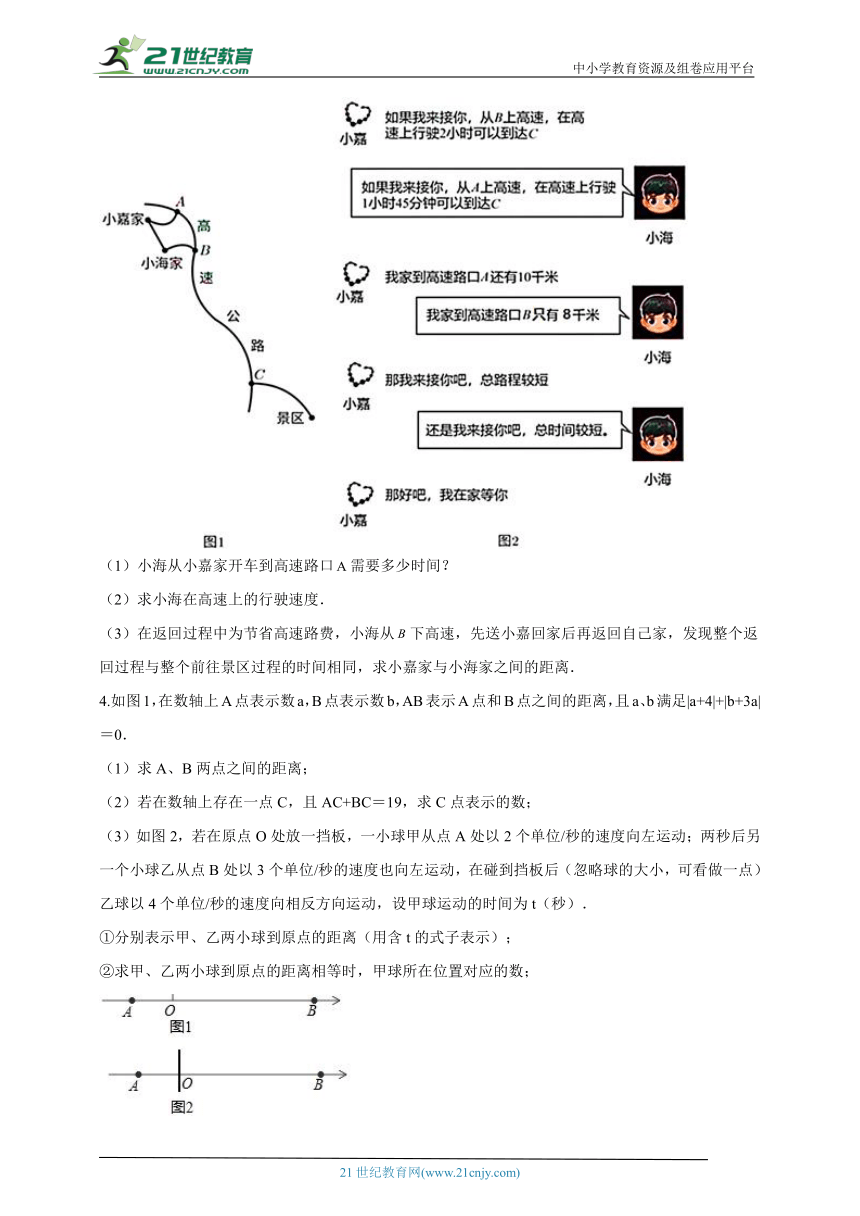
3.小嘉和小海相约去某景区游玩,其地理位置及部分路线如图1.,,为三个高速路口,已知高速路段的路程为,在高速上小海每小时可比小嘉多行驶,在其余道路上两人的开车速度均为.他俩的微信对话部分信息如图2.(注:在高速上匀速行驶)
(1)小海从小嘉家开车到高速路口需要多少时间?
(2)求小海在高速上的行驶速度.
(3)在返回过程中为节省高速路费,小海从下高速,先送小嘉回家后再返回自己家,发现整个返回过程与整个前往景区过程的时间相同,求小嘉家与小海家之间的距离.
4.如图1,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+4|+|b+3a|=0.
(1)求A、B两点之间的距离;
(2)若在数轴上存在一点C,且AC+BC=19,求C点表示的数;
(3)如图2,若在原点O处放一挡板,一小球甲从点A处以2个单位/秒的速度向左运动;两秒后另一个小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)乙球以4个单位/秒的速度向相反方向运动,设甲球运动的时间为t(秒).
①分别表示甲、乙两小球到原点的距离(用含t的式子表示);
②求甲、乙两小球到原点的距离相等时,甲球所在位置对应的数;
5.甲、乙两车从 A,B 两地同时出发,沿同一条路线相向匀速行驶.出发后经 2 小时两车相遇, 已知在相遇时乙车比甲车多行驶了 30 千米.相遇后若乙车继续往前行驶,还需 1.6 小时才能 到达 A 地.
(1)求甲,乙两车行驶的速度分别是多少?
(2)如果相遇后甲车继续前往 B 地(到达后停止行驶),乙车在相遇点休息了 10 分钟后,按 原速度立即返回 B 地,问乙车重新出发后多长时间,两车相距 5 千米?
6.一段公路米,点是公路上的充电站,其中,现在有甲、乙两辆智能垃圾清扫车从充电站同时出发(如图所示),沿相反方向分别开始对路段的清扫工作,其中甲的速度为每分钟6米,乙的速度为每分钟12米,两车清扫完各自路段(即完成清扫任务后)按原来速度原路返回到站充电.
(1)甲车清扫完路段需共______分钟;乙车清扫完路段需花______分钟;
(2)当两车之间的距离在60米以内时,能互相接收到对方信号,请问接收不到对方信号的时间总共有多长?
(3)某一天早上6点两车同时开始清扫工作,但是当出发25分钟后,乙车发生故障,此时甲车接到指令,完成自己路段的清扫工作后,支援乙车完成路段的剩余工作任务.若甲车速度始终不变,问能否在当天上午9点前完成全部清扫工作?若不能完成,那么甲车在完成自己路段的清扫工作后需要将速度提高到每分钟多少米才能恰好在规定时间内完成全部清扫任务?
7.已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长(单位长度),慢车长(单位长度),设正在行驶途中的一时刻,如图,以两车之间的某点为原点,取向右方向为正方向画数轴,此时快车头在数轴上表示的数是,慢车头在数轴上表示的数是.若快车以6个单位长度秒的速度向右匀速继续行驶,同时慢车以2个单位长度/秒的速度向左匀速继续行驶,且与互为相反数.
(1)求此时刻快车头与慢车头之间相距多少单位长度?
(2)从此时刻开始算起,问再行驶多少秒钟两列火车行驶到车头相距8个单位长度?
8.甲、乙两位同学沿着环湖绿道锻炼,A是其中的一个起点,B、C两点为绿道中的休息点,绿道分为AB、AC、BC三段,AC和AB之间的路线长分别为10km和6km,B、C两点之间有一座桥,长度为3km,甲沿着A→B→C→A的线路,以6km/h的速度走路,乙沿着A→C→B→A的线路,以4km/h的速度走路,两人经过3小时后相遇,甲出发1.5小时后,丙以12km/h的速度骑车去追甲.
(1) 求环形跑道中BC段的长度;
(2) 当丙以最快的方式追上甲时,求追上点到C的距离;
(3) 若甲、乙、丙沿着环湖绿道通行,当三人都没有两两相遇时,设甲走过的路程为,乙走过的路程为,丙走过的路程为,请判断是否为定值,若为定值,求出该定值;若不是定值,请说明理由.
参考答案
1.【答案】(1)答案见解析;(2)千米/小时;(3)
【分析】(1)凉亭可在观景台的左边,也可在观景台的右边,小卖部可在凉亭的左边,也可在凉亭的右边,由此标出小卖部所有可能的位置;
(2)根据路程、速度、时间的关系即可求解;
(3)根据路程、速度、时间的关系表示出方方同学上山实际时间,计算出下山前总花费时间从而得出下山的时间,根据路程相等列出方程,解方程即可.
【详解】解:(1)设Q表示凉亭的位置,凉亭可在观景台的左边,也可在观景台的右边,则可用数字表示,可用数字表示,
小卖部可在凉亭的左边,也可在凉亭的右边,小卖部所有可能的位置,可用数字表示,可用数字表示,可用数字表示,可用数字表示,
如图,
;
(2)圆圆下山用了小时,全程的平均速度为千米/小时.
(3)上山实际时间:(分),
下山前总花费时间:(分),
上午到下午共300分,
(分).
设上山的速度是千米/小时,根据题意得
,
解得.
2.【答案】(1)甲车到B站用时16分钟,乙车到B站用时8分钟;(2)8:14两车相遇;(3)小时或小时.
【分析】(1)根据时间=路程÷速度列式即可求值;
(2)根据题意列出方程,进行求值即可 ;
(3)分三种情况:①两车相遇前,乙车刚到B站时,两车相距4千米,②两车相遇后,乙车经过B站,甲车还没有到B站时,③两车相遇后,甲乙两车都经过B站时,分别列出式子表示即可;
【详解】解:(1)甲车到B站用时(小时)=16(分钟).
乙车到B站用时(小时)=8(分钟).
(2)由题意可列方程
解得:小时=14分钟.
所以两车在8:14两车相遇.
(3)分三种情况:
①两车相遇前,乙车刚到B站时,两车相距4千米,
此时(小时)
②两车相遇后,乙车经过B站,甲车还没有到B站时,
,
解得:,此时甲车已经过B站,与假设矛盾(舍去).
③两车相遇后,甲乙两车都经过B站时,
,
解得:(小时)
综上所述:当小时或小时时,两车相距4千米
3.【答案】(1)10分;(2)小海在高速上的速度为;(3)小嘉家与小海家之间的距离为.
【分析】(1)根据“时间=路程÷速度”计算即可;
(2)设小海在高速上的速度为,找出题目中的等量关系为:小海在高速上行驶的路程(AC段)=小嘉在高速上行驶的路程(BC段)+10,据此列出方程,求解即可得出结论;
(3)根据整个返回过程与整个前往景区过程的时间相同,先确定前往路线和返回路线,排除往返路线中的重合部分,则可得到等量关系为:高速出口B到小海家的行驶时间+小海家到小嘉家行驶的时间=小嘉家到高速出口A的行驶时间+高速公路AB段行驶的时间,设小嘉家与小海家之间的距离为,则利用路程与速度表示出各段的时间可列出方程,即可求出结果.
【详解】解:(1)(小时),
(分)
答:小海从小嘉家开车到高速路口需要10分钟;
(2)设小海在高速上的速度为,则小嘉在高速上的速度为,依题意得:
1小时45分=1.75小时,
解得:
答:小海在高速上的速度为.
(3)前往路线:小海家小嘉家ABC景区,
返回中线:景区CB小海家小嘉家小海家.
设小嘉家与小海家之间的距离为,根据题意,得:
解得:,
答:小嘉家与小海家之间的距离为.
4.【答案】(1)A、B两点之间的距离是16;(2)点C不可能线段AB上,则C点可能在线段BA的延长线上或线段AB的延长线上,当AC+BC=19,C表示的数为或;(3)①乙球到原点的距离为:12﹣3(t﹣2);甲球与原点的距离为:2t+4;②甲、乙两小球到原点的距离相等时,甲球所在位置对应的数为﹣或﹣48.
【分析】(1)先根据非负数的性质求出a、b的值,再根据两点间的距离公式即可求得A、B两点之间的距离;
(2)分C点在线段BA延长线上和线段AB延长线上两种情况讨论即可求解;
(3)①甲球到原点的距离=甲球运动的路程+OA的长,乙球到原点的距离分两种情况:(Ⅰ)乙球从点B处开始向左运动,一直到原点O,此时OB的长度﹣乙球运动的路程即为乙球到原点的距离;(Ⅱ)乙球从原点O处开始向右运动,此时乙球运动的路程﹣OB的长度即为乙球到原点的距离;
②按①分两种情况根据甲、乙两小球到原点的距离相等列出关于t的方程,解方程即可.
【详解】解:(1)∵|a+4|+|b+3b|=0,
∴a+4=0,b+3a=0,
∴a=﹣4,b=﹣3a=12,
∴AB=|b﹣a|=|12﹣(﹣4)|=16
∴A、B两点之间的距离是16.
(2)设数轴上点C表示的数为c
∴AC=|c﹣a|=|c+4|,BC=|c﹣b|=|c﹣12|
∵AC+BC=19
∴|c+4|+|c﹣12|=19
∵AB=16<19
∴点C不可能线段AB上,则C点可能在线段BA的延长线上或线段AB的延长线上.
①当C点在线段BA延长线上时,则有c≤﹣4,
∴|c+4|=﹣(c+4),|c﹣12|=﹣(c﹣12)
∴﹣(c+4)﹣(c﹣12)=19
解得:c=
②当C点在线段AB的延长线上时,则有c>12,
∴|c+4|=c+4,|c﹣12|=c﹣12
∴c+4+c﹣12=19
解得:c=
综上所说,当AC+BC=19,C表示的数为或.
(3)①∵甲球运动的路程为:2 t=2t,OA=4
∴甲球与原点的距离为:2t+4
乙球到原点的距离分两种情况:
(Ⅰ)当0<t≤4时,乙球从点B处开始向左运动,一直到原点O,
∵OB=12,乙球运动的路程为:3 t=3t,
∴乙球到原点的距离为:12﹣3(t﹣2);
(Ⅱ)当t>4时,乙球从原点O处开始一直向右运动,
∴乙球到原点的距离为:3(t﹣2)﹣12.
②当0<t≤4时,得2t+4=12﹣3(t﹣2),
解得:t=
∴﹣4﹣2t=
当t>4时,得2t+4=3(t﹣2)﹣12,
解得:t=22
∴﹣4﹣2t=﹣48
综上所述,甲、乙两小球到原点的距离相等时,甲球所在位置对应的数为﹣或﹣48.
5.【答案】(1)甲的速度为60千米/小时,乙的速度为75千米/小时;(2)小时或1小时.
【分析】解:(1)设甲的速度为每小时千米,则乙的速度为每小时(x+)千米,根据“相遇后若乙车继续往前行驶,还需 1.6 小时才能 到达 A 地”,可知甲2小时行驶的路程等于乙1.6 小时行驶的路程,列出方程求出甲的速度,进而可得乙的速度;
(2)设乙车重新出发后小时两车相距5千米,分两种情况:若乙车在甲车后5千米,则甲(y+)小时行驶的路程=乙y 小时行驶的路程+5;若乙车在甲车前5千米,则乙y小时行驶的路程-5=甲(y+) 小时行驶的路程,列出方程求解即可.
【详解】(1)设甲的速度为每小时千米,则乙的速度为每小时(x+)千米
由题意可得2x=1.6(x+)
解得x=60
∴x+=75
答:甲的速度为60千米/小时,乙的速度为75千米/小时.
(2)设乙车重新出发后y小时两车相距5千米
乙车重新出发后,甲车到达地还需要的时间为 = 小时
若乙车在甲车后5千米,
则75y+5=60(y+)
解得y=
若乙车在甲车前5千米
则75y-5=60(y+)
解得
即乙车重新出发后经过小时或1小时两车相距5千米.
6.【答案】(1);(2)接收不到对方信号的时间总共有:分钟;(3)当天上午9点前不能完成全部清扫工作,甲车在完成自己路段的清扫工作后需要将速度提高到每分钟米,才能恰好在规定时间内完成全部清扫任务.
【分析】(1)先求解的长度,再利用路程除以速度即可得到答案;
(2)先求解出发清扫时能接收到信号的时间为:分钟,再计算甲车回到点时,用时分钟,再确定乙车的位置,计算乙车在回程过程中能接收到信号的时间,从而可得答案;
(3)当分钟时,乙车清扫了米,剩余工作量为米,由甲车的速度不变,再求解甲车从开始清扫到帮助乙车完成任务所花时间为:分钟,从而可得答案;再由甲车清扫完路段需共分钟;设甲车的速度提高到每分钟米,列方程 再解方程可得答案.
【详解】解:(1) (米), ,
(米),(米),
甲车清扫完路段需共分钟;乙车清扫完路段需花分钟;
故答案为:
(2)当两车出发清扫时,有(分钟)能接收信号,
当甲车回到点时,用时(分钟),
此时乙车距点(米)
所以乙车在回到点能接收到信号的时间为:(分钟),
所以:接收不到对方信号的时间总共有:(分钟),
(3)当分钟时,乙车清扫了(米),剩余工作量为米,
若甲车的速度不变,则甲车从开始清扫到帮助乙车完成任务所花时间为:
(分钟),
>,
当天上午9点前不能完成全部清扫工作.
甲车清扫完路段需共分钟;
设甲车的速度提高到每分钟米,则
答:甲车在完成自己路段的清扫工作后需要将速度提高到每分钟米,才能恰好在规定时间内完成全部清扫任务.
7.【答案】(1)此时刻快车头与慢车头之间相距24个单位长度;(2)再行驶2秒或4秒钟两列火车行驶到车头相距8个单位长度.
【分析】(1)由题意得,根据非负数的性质求出a,b即可解决问题;
(2)设再行驶t秒钟两列火车行驶到车头相距8个单位长度,分相遇前和相遇后两种情况,分别列方程求解即可.
【详解】解:(1)由题意得:,
∴且,
∴,,
17-(-7)=24,
答:此时刻快车头与慢车头之间相距24个单位长度;
(2)设再行驶t秒钟两列火车行驶到车头相距8个单位长度,
①当车头相遇前相距8个单位长度时,
由题意得:6t+2t=24-8,
解得:t=2;
②当车头相遇后相距8个单位长度时,
由题意得:6t+2t=24+8,
解得:t=4;
答:再行驶2秒或4秒钟两列火车行驶到车头相距8个单位长度.
8.【答案】(1)14km;(2)2km;(3)为定值18km,理由见解析.
【分析】(1)设环形跑道中BC段的长度为xkm,根据“甲乙路程和=环形跑道总路程”列方程求解即可;
(2)设丙x小时追上甲.根据“甲丙的路程差=甲先走的路程”列方程求初x的值,然后根据“追上点到C的距离=环形跑道AB的长度+环形跑道BC的长度-甲所走的路程”计算即可;
(3)设丙的时间为x小时,则甲、乙的时间为(x+1.5)小时.表示出甲走过的路程为,乙走过的路程为,丙走过的路程为.代入计算即可得出结论.
【详解】(1)设环形跑道中BC段的长度为xkm,根据题意得:
3(6+4)=6+x+10
解得:x=14.
答:环形跑道中BC段的长度14km.
(2)设丙x小时追上甲.根据题意得:
(12-6)x=1.5×6
解得:x=1.5.
追上点到C的距离=6+14-6×(1.5+1.5)=2(km).
答:追上点到C的距离为2km.
(3)设丙的时间为x小时,则甲、乙的时间为(x+1.5)小时.根据题意得:
甲走过的路程为=6x+9,乙走过的路程为=4(x+1.5)=4x+6,丙走过的路程为=12x.==6x+9+6x+9-12x=18(km).
故为定值18km.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版七年级上册数学 一元一次方程应用行程问题 专题训练
1.某景区门票上绘制了简易游览图(如图),从游客中心到观景台有山路,从观景台到山顶有山路,圆圆同学从导游口中得知:离观景台处有一个凉亭,离凉亭处有一个小卖部.
(1)圆圆同学把这张图中的游览线路抽象成一条数轴,其中游客中心是原点,往山顶方向为正方向,为1个单位长度,请在数轴上标出小卖部所有可能的位置,并用数字表示出来.
(2)圆圆同学上山时从游客中心到山顶共用了小时,下山时从山顶到游客中心的平均速度为千米/小时,求圆圆同学上山、下山全程的平均速度(用含和的代数式表示).
(3)若凉亭在观景台到山顶的途中,方方同学上午从游客中心出发匀速上山,于到达观景台,在观景台停留30分钟后,以同样的速度继续上山,途中又在凉亭休息了15分钟,到山顶游玩了35分钟后下山(下山途中不再停留),为了在下午准时回到游客中心,方方同学下山的速度比上山的速度快,求的值.
2.如图,城乡公交车行驶在笔直的公路上,这条路上有A,B,C三个站点,已知相邻两站之间的距离分别为千米,千米,且每个站点的停靠时间为4分钟.已知甲、乙两车于上午8:00分别从A站,C站出发相向而行,两车的速度均为30千米/小时,设两车出发t小时后,问:
(1)甲、乙两车到达B站分别用时多少?
(2)求两车相遇的时刻.
(3)当两车相距4千米时,求t的值.
3.小嘉和小海相约去某景区游玩,其地理位置及部分路线如图1.,,为三个高速路口,已知高速路段的路程为,在高速上小海每小时可比小嘉多行驶,在其余道路上两人的开车速度均为.他俩的微信对话部分信息如图2.(注:在高速上匀速行驶)
(1)小海从小嘉家开车到高速路口需要多少时间?
(2)求小海在高速上的行驶速度.
(3)在返回过程中为节省高速路费,小海从下高速,先送小嘉回家后再返回自己家,发现整个返回过程与整个前往景区过程的时间相同,求小嘉家与小海家之间的距离.
4.如图1,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+4|+|b+3a|=0.
(1)求A、B两点之间的距离;
(2)若在数轴上存在一点C,且AC+BC=19,求C点表示的数;
(3)如图2,若在原点O处放一挡板,一小球甲从点A处以2个单位/秒的速度向左运动;两秒后另一个小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)乙球以4个单位/秒的速度向相反方向运动,设甲球运动的时间为t(秒).
①分别表示甲、乙两小球到原点的距离(用含t的式子表示);
②求甲、乙两小球到原点的距离相等时,甲球所在位置对应的数;
5.甲、乙两车从 A,B 两地同时出发,沿同一条路线相向匀速行驶.出发后经 2 小时两车相遇, 已知在相遇时乙车比甲车多行驶了 30 千米.相遇后若乙车继续往前行驶,还需 1.6 小时才能 到达 A 地.
(1)求甲,乙两车行驶的速度分别是多少?
(2)如果相遇后甲车继续前往 B 地(到达后停止行驶),乙车在相遇点休息了 10 分钟后,按 原速度立即返回 B 地,问乙车重新出发后多长时间,两车相距 5 千米?
6.一段公路米,点是公路上的充电站,其中,现在有甲、乙两辆智能垃圾清扫车从充电站同时出发(如图所示),沿相反方向分别开始对路段的清扫工作,其中甲的速度为每分钟6米,乙的速度为每分钟12米,两车清扫完各自路段(即完成清扫任务后)按原来速度原路返回到站充电.
(1)甲车清扫完路段需共______分钟;乙车清扫完路段需花______分钟;
(2)当两车之间的距离在60米以内时,能互相接收到对方信号,请问接收不到对方信号的时间总共有多长?
(3)某一天早上6点两车同时开始清扫工作,但是当出发25分钟后,乙车发生故障,此时甲车接到指令,完成自己路段的清扫工作后,支援乙车完成路段的剩余工作任务.若甲车速度始终不变,问能否在当天上午9点前完成全部清扫工作?若不能完成,那么甲车在完成自己路段的清扫工作后需要将速度提高到每分钟多少米才能恰好在规定时间内完成全部清扫任务?
7.已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长(单位长度),慢车长(单位长度),设正在行驶途中的一时刻,如图,以两车之间的某点为原点,取向右方向为正方向画数轴,此时快车头在数轴上表示的数是,慢车头在数轴上表示的数是.若快车以6个单位长度秒的速度向右匀速继续行驶,同时慢车以2个单位长度/秒的速度向左匀速继续行驶,且与互为相反数.
(1)求此时刻快车头与慢车头之间相距多少单位长度?
(2)从此时刻开始算起,问再行驶多少秒钟两列火车行驶到车头相距8个单位长度?
8.甲、乙两位同学沿着环湖绿道锻炼,A是其中的一个起点,B、C两点为绿道中的休息点,绿道分为AB、AC、BC三段,AC和AB之间的路线长分别为10km和6km,B、C两点之间有一座桥,长度为3km,甲沿着A→B→C→A的线路,以6km/h的速度走路,乙沿着A→C→B→A的线路,以4km/h的速度走路,两人经过3小时后相遇,甲出发1.5小时后,丙以12km/h的速度骑车去追甲.
(1) 求环形跑道中BC段的长度;
(2) 当丙以最快的方式追上甲时,求追上点到C的距离;
(3) 若甲、乙、丙沿着环湖绿道通行,当三人都没有两两相遇时,设甲走过的路程为,乙走过的路程为,丙走过的路程为,请判断是否为定值,若为定值,求出该定值;若不是定值,请说明理由.
参考答案
1.【答案】(1)答案见解析;(2)千米/小时;(3)
【分析】(1)凉亭可在观景台的左边,也可在观景台的右边,小卖部可在凉亭的左边,也可在凉亭的右边,由此标出小卖部所有可能的位置;
(2)根据路程、速度、时间的关系即可求解;
(3)根据路程、速度、时间的关系表示出方方同学上山实际时间,计算出下山前总花费时间从而得出下山的时间,根据路程相等列出方程,解方程即可.
【详解】解:(1)设Q表示凉亭的位置,凉亭可在观景台的左边,也可在观景台的右边,则可用数字表示,可用数字表示,
小卖部可在凉亭的左边,也可在凉亭的右边,小卖部所有可能的位置,可用数字表示,可用数字表示,可用数字表示,可用数字表示,
如图,
;
(2)圆圆下山用了小时,全程的平均速度为千米/小时.
(3)上山实际时间:(分),
下山前总花费时间:(分),
上午到下午共300分,
(分).
设上山的速度是千米/小时,根据题意得
,
解得.
2.【答案】(1)甲车到B站用时16分钟,乙车到B站用时8分钟;(2)8:14两车相遇;(3)小时或小时.
【分析】(1)根据时间=路程÷速度列式即可求值;
(2)根据题意列出方程,进行求值即可 ;
(3)分三种情况:①两车相遇前,乙车刚到B站时,两车相距4千米,②两车相遇后,乙车经过B站,甲车还没有到B站时,③两车相遇后,甲乙两车都经过B站时,分别列出式子表示即可;
【详解】解:(1)甲车到B站用时(小时)=16(分钟).
乙车到B站用时(小时)=8(分钟).
(2)由题意可列方程
解得:小时=14分钟.
所以两车在8:14两车相遇.
(3)分三种情况:
①两车相遇前,乙车刚到B站时,两车相距4千米,
此时(小时)
②两车相遇后,乙车经过B站,甲车还没有到B站时,
,
解得:,此时甲车已经过B站,与假设矛盾(舍去).
③两车相遇后,甲乙两车都经过B站时,
,
解得:(小时)
综上所述:当小时或小时时,两车相距4千米
3.【答案】(1)10分;(2)小海在高速上的速度为;(3)小嘉家与小海家之间的距离为.
【分析】(1)根据“时间=路程÷速度”计算即可;
(2)设小海在高速上的速度为,找出题目中的等量关系为:小海在高速上行驶的路程(AC段)=小嘉在高速上行驶的路程(BC段)+10,据此列出方程,求解即可得出结论;
(3)根据整个返回过程与整个前往景区过程的时间相同,先确定前往路线和返回路线,排除往返路线中的重合部分,则可得到等量关系为:高速出口B到小海家的行驶时间+小海家到小嘉家行驶的时间=小嘉家到高速出口A的行驶时间+高速公路AB段行驶的时间,设小嘉家与小海家之间的距离为,则利用路程与速度表示出各段的时间可列出方程,即可求出结果.
【详解】解:(1)(小时),
(分)
答:小海从小嘉家开车到高速路口需要10分钟;
(2)设小海在高速上的速度为,则小嘉在高速上的速度为,依题意得:
1小时45分=1.75小时,
解得:
答:小海在高速上的速度为.
(3)前往路线:小海家小嘉家ABC景区,
返回中线:景区CB小海家小嘉家小海家.
设小嘉家与小海家之间的距离为,根据题意,得:
解得:,
答:小嘉家与小海家之间的距离为.
4.【答案】(1)A、B两点之间的距离是16;(2)点C不可能线段AB上,则C点可能在线段BA的延长线上或线段AB的延长线上,当AC+BC=19,C表示的数为或;(3)①乙球到原点的距离为:12﹣3(t﹣2);甲球与原点的距离为:2t+4;②甲、乙两小球到原点的距离相等时,甲球所在位置对应的数为﹣或﹣48.
【分析】(1)先根据非负数的性质求出a、b的值,再根据两点间的距离公式即可求得A、B两点之间的距离;
(2)分C点在线段BA延长线上和线段AB延长线上两种情况讨论即可求解;
(3)①甲球到原点的距离=甲球运动的路程+OA的长,乙球到原点的距离分两种情况:(Ⅰ)乙球从点B处开始向左运动,一直到原点O,此时OB的长度﹣乙球运动的路程即为乙球到原点的距离;(Ⅱ)乙球从原点O处开始向右运动,此时乙球运动的路程﹣OB的长度即为乙球到原点的距离;
②按①分两种情况根据甲、乙两小球到原点的距离相等列出关于t的方程,解方程即可.
【详解】解:(1)∵|a+4|+|b+3b|=0,
∴a+4=0,b+3a=0,
∴a=﹣4,b=﹣3a=12,
∴AB=|b﹣a|=|12﹣(﹣4)|=16
∴A、B两点之间的距离是16.
(2)设数轴上点C表示的数为c
∴AC=|c﹣a|=|c+4|,BC=|c﹣b|=|c﹣12|
∵AC+BC=19
∴|c+4|+|c﹣12|=19
∵AB=16<19
∴点C不可能线段AB上,则C点可能在线段BA的延长线上或线段AB的延长线上.
①当C点在线段BA延长线上时,则有c≤﹣4,
∴|c+4|=﹣(c+4),|c﹣12|=﹣(c﹣12)
∴﹣(c+4)﹣(c﹣12)=19
解得:c=
②当C点在线段AB的延长线上时,则有c>12,
∴|c+4|=c+4,|c﹣12|=c﹣12
∴c+4+c﹣12=19
解得:c=
综上所说,当AC+BC=19,C表示的数为或.
(3)①∵甲球运动的路程为:2 t=2t,OA=4
∴甲球与原点的距离为:2t+4
乙球到原点的距离分两种情况:
(Ⅰ)当0<t≤4时,乙球从点B处开始向左运动,一直到原点O,
∵OB=12,乙球运动的路程为:3 t=3t,
∴乙球到原点的距离为:12﹣3(t﹣2);
(Ⅱ)当t>4时,乙球从原点O处开始一直向右运动,
∴乙球到原点的距离为:3(t﹣2)﹣12.
②当0<t≤4时,得2t+4=12﹣3(t﹣2),
解得:t=
∴﹣4﹣2t=
当t>4时,得2t+4=3(t﹣2)﹣12,
解得:t=22
∴﹣4﹣2t=﹣48
综上所述,甲、乙两小球到原点的距离相等时,甲球所在位置对应的数为﹣或﹣48.
5.【答案】(1)甲的速度为60千米/小时,乙的速度为75千米/小时;(2)小时或1小时.
【分析】解:(1)设甲的速度为每小时千米,则乙的速度为每小时(x+)千米,根据“相遇后若乙车继续往前行驶,还需 1.6 小时才能 到达 A 地”,可知甲2小时行驶的路程等于乙1.6 小时行驶的路程,列出方程求出甲的速度,进而可得乙的速度;
(2)设乙车重新出发后小时两车相距5千米,分两种情况:若乙车在甲车后5千米,则甲(y+)小时行驶的路程=乙y 小时行驶的路程+5;若乙车在甲车前5千米,则乙y小时行驶的路程-5=甲(y+) 小时行驶的路程,列出方程求解即可.
【详解】(1)设甲的速度为每小时千米,则乙的速度为每小时(x+)千米
由题意可得2x=1.6(x+)
解得x=60
∴x+=75
答:甲的速度为60千米/小时,乙的速度为75千米/小时.
(2)设乙车重新出发后y小时两车相距5千米
乙车重新出发后,甲车到达地还需要的时间为 = 小时
若乙车在甲车后5千米,
则75y+5=60(y+)
解得y=
若乙车在甲车前5千米
则75y-5=60(y+)
解得
即乙车重新出发后经过小时或1小时两车相距5千米.
6.【答案】(1);(2)接收不到对方信号的时间总共有:分钟;(3)当天上午9点前不能完成全部清扫工作,甲车在完成自己路段的清扫工作后需要将速度提高到每分钟米,才能恰好在规定时间内完成全部清扫任务.
【分析】(1)先求解的长度,再利用路程除以速度即可得到答案;
(2)先求解出发清扫时能接收到信号的时间为:分钟,再计算甲车回到点时,用时分钟,再确定乙车的位置,计算乙车在回程过程中能接收到信号的时间,从而可得答案;
(3)当分钟时,乙车清扫了米,剩余工作量为米,由甲车的速度不变,再求解甲车从开始清扫到帮助乙车完成任务所花时间为:分钟,从而可得答案;再由甲车清扫完路段需共分钟;设甲车的速度提高到每分钟米,列方程 再解方程可得答案.
【详解】解:(1) (米), ,
(米),(米),
甲车清扫完路段需共分钟;乙车清扫完路段需花分钟;
故答案为:
(2)当两车出发清扫时,有(分钟)能接收信号,
当甲车回到点时,用时(分钟),
此时乙车距点(米)
所以乙车在回到点能接收到信号的时间为:(分钟),
所以:接收不到对方信号的时间总共有:(分钟),
(3)当分钟时,乙车清扫了(米),剩余工作量为米,
若甲车的速度不变,则甲车从开始清扫到帮助乙车完成任务所花时间为:
(分钟),
>,
当天上午9点前不能完成全部清扫工作.
甲车清扫完路段需共分钟;
设甲车的速度提高到每分钟米,则
答:甲车在完成自己路段的清扫工作后需要将速度提高到每分钟米,才能恰好在规定时间内完成全部清扫任务.
7.【答案】(1)此时刻快车头与慢车头之间相距24个单位长度;(2)再行驶2秒或4秒钟两列火车行驶到车头相距8个单位长度.
【分析】(1)由题意得,根据非负数的性质求出a,b即可解决问题;
(2)设再行驶t秒钟两列火车行驶到车头相距8个单位长度,分相遇前和相遇后两种情况,分别列方程求解即可.
【详解】解:(1)由题意得:,
∴且,
∴,,
17-(-7)=24,
答:此时刻快车头与慢车头之间相距24个单位长度;
(2)设再行驶t秒钟两列火车行驶到车头相距8个单位长度,
①当车头相遇前相距8个单位长度时,
由题意得:6t+2t=24-8,
解得:t=2;
②当车头相遇后相距8个单位长度时,
由题意得:6t+2t=24+8,
解得:t=4;
答:再行驶2秒或4秒钟两列火车行驶到车头相距8个单位长度.
8.【答案】(1)14km;(2)2km;(3)为定值18km,理由见解析.
【分析】(1)设环形跑道中BC段的长度为xkm,根据“甲乙路程和=环形跑道总路程”列方程求解即可;
(2)设丙x小时追上甲.根据“甲丙的路程差=甲先走的路程”列方程求初x的值,然后根据“追上点到C的距离=环形跑道AB的长度+环形跑道BC的长度-甲所走的路程”计算即可;
(3)设丙的时间为x小时,则甲、乙的时间为(x+1.5)小时.表示出甲走过的路程为,乙走过的路程为,丙走过的路程为.代入计算即可得出结论.
【详解】(1)设环形跑道中BC段的长度为xkm,根据题意得:
3(6+4)=6+x+10
解得:x=14.
答:环形跑道中BC段的长度14km.
(2)设丙x小时追上甲.根据题意得:
(12-6)x=1.5×6
解得:x=1.5.
追上点到C的距离=6+14-6×(1.5+1.5)=2(km).
答:追上点到C的距离为2km.
(3)设丙的时间为x小时,则甲、乙的时间为(x+1.5)小时.根据题意得:
甲走过的路程为=6x+9,乙走过的路程为=4(x+1.5)=4x+6,丙走过的路程为=12x.==6x+9+6x+9-12x=18(km).
故为定值18km.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
