浙教版数学九年级上册 第三章 圆的基本性质(含答案)
文档属性
| 名称 | 浙教版数学九年级上册 第三章 圆的基本性质(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 00:00:00 | ||
图片预览


文档简介
第三章 圆的基本性质
班级 学号 姓名 得分
一、选择题(本大题有10小题,每小题3分,共30分)
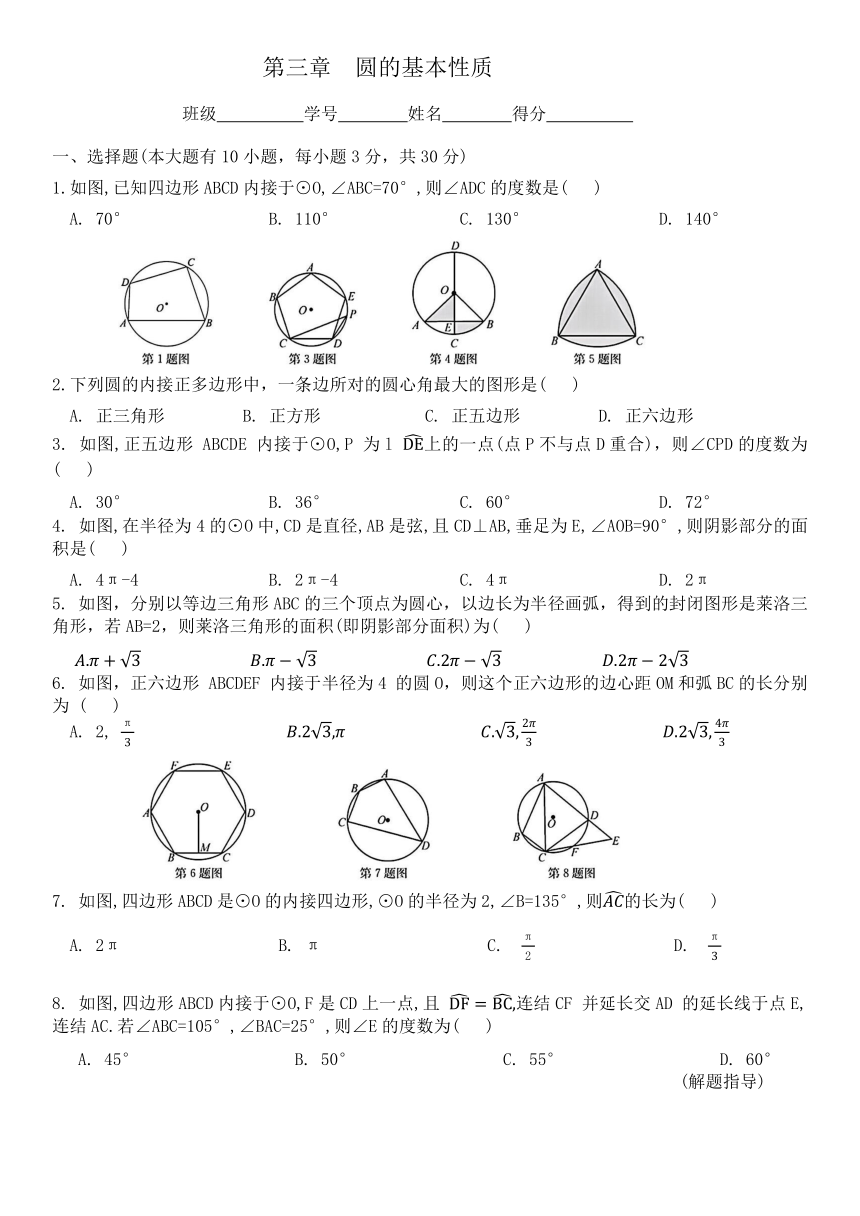
1.如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )
A. 70° B. 110° C. 130° D. 140°
2.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形
3. 如图,正五边形 ABCDE 内接于⊙O,P 为l 上的一点(点P不与点D重合),则∠CPD的度数为( )
A. 30° B. 36° C. 60° D. 72°
4. 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为E,∠AOB=90°,则阴影部分的面积是( )
A. 4π-4 B. 2π-4 C. 4π D. 2π
5. 如图,分别以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为( )
6. 如图,正六边形 ABCDEF 内接于半径为4 的圆O,则这个正六边形的边心距OM和弧BC的长分别为 ( )
A. 2,
7. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长为( )
A. 2π B. π C. D.
8. 如图,四边形ABCD内接于⊙O,F是CD上一点,且 连结CF 并延长交AD 的延长线于点E,连结AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A. 45° B. 50° C. 55° D. 60°
(解题指导)
9. 如图,四边形 ABCD 内接于⊙O,AE⊥CB交CB 的延长线于点E,若 BA 平分∠DBE,AD=5,CE 则AE等于( )
A. 3
10. 如图所示,一条公路的转弯处是一段圆弧(即图中点 O是 的圆心),其中 CD=600m,点E为CD上一点,且OE⊥CD,垂足为F, 则这段弯路的长度为( )
A. 200πm
B. 100πm
C. 400πm
D. 300πm
二、填空题(本大题有6小题,每小题4分,共24分)
11.若扇形的圆心角为45°,半径为3,则该扇形的弧长为 .
12. 如图,在平行四边形ABCD中,AB13. 如图,扇形AOB的圆心角为直角,边长为1的正方形OCDE的顶点C,E,D分别在OA,OB, 上,过点A作 AF⊥ED,交ED的延长线于点F,则图中阴影部分的面积等于 .
14. 刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.若用圆的内接正十二边形的面积S 来近似估计⊙O的面积S,设⊙O的半径为1,则
15. 如图,已知等边三角形ABC的边长为6,以AB为直径的⊙O与边AC,BC 分别交于D,E 两点,则劣弧. 的长为 .
16. 如图,四边形 ABCD 内接于⊙O,∠DAB=130°,连结OC.点 P 是半径OC 上任意一点,连结DP,BP,则∠BPD可能为 度(写出一个即可).
三、解答题(本大题有8小题,共66分)
17.(6分)已知扇形的圆心角为120°,弧长为20πcm,求扇形的面积.
18.(6分)如图所示,四边形 ABCD内接于⊙O,并且AD是⊙O的直径,C是BD的中点,AB 和DC 的延长线交于⊙O外一点E.求证:
19. (6分)如图,AB为⊙O的直径, 于点E,交⊙O于点C,D,( 于点 F.
(1)请写出三条与 BC有关的正确结论;
(2)当 时,求图中阴影部分的面积.
20.(8分)如图,点O是线段AB 的中点,根据要求完成下题:
(1)在图中完成下面的操作:
第一步,以AB为直径画出⊙O;
第二步,以B为圆心,以 BO为半径画圆弧,交⊙O于点C,连结CA,CO.
(2)设 ,求扇形 AOC的面积(结果保留π).
21.(8分)如图,⊙O是 的外接圆,BC的垂直平分线与 相交于D 点,若
求AD的度数.
22.(10分)如图,已知 是⊙O的内接三角形,AD 是⊙O的直径,连结 BD,BC平分
(1)求证:
(2)若 求 的长.
23.(10分)如图,在边长为1的正方形组成的网格中, 的顶点均在格点上,其中点 A(5,4), B(1,3),将 绕点O逆时针旋转 后得到
(1)画出
(2)求在旋转过程中线段AB扫过的图形的面积.
24.(12分)正方形 ABCD 内接于⊙O,如图所示,在劣弧AB上取一点 E,连结DE,BE,过点 D 作 交⊙O于点F,连结BF,AF,且AF与DE 相交于点G.
求证:(1)四边形EBFD是矩形;
第三章 圆的基本性质
1. B 2. A 3. B 4. D 5. D 6. D 7. B
8. B 9. D 10. A 11
14. π-3 15. π 16. 60(答案不唯一,大于或等于50且小于或等于100即可)
17. 解:设扇形的半径为 Rcm, ∴面积 ∴扇形面积为
18. 证明:如图,连结 AC.∵AD是⊙O的直径, ∠ACE.∵四边形 ABCD 内接于⊙O, 又∵ .∠EBC=∠D.∵C是 的中点,∴∠1=∠2,又∵ ∴∠E=∠D,∴∠EBC=∠E,∴BC=EC.
19. 解:(1)①BC=BD,②BC∥OF,③BC=2OF等(合理即可). (2)连结OC,∵OA=OC,∴∠A=∠ACO.∵∠A=∠D=30°,∠ACO=30°,AB=
20. 解:(1)如图. (2)如图,连结BC,则 BC=BO=OC,∴△BOC是等边三角形,∴∠BOC=60°,∴∠AOC=120°,∴S点形AOC =
21. 解:如图,连结OB,OC,AO,BC的垂直平分线必过点 O,设DO交 BC 于 点 E, ∴∠BOE = ∴∠BOE=∠BAC,∵∠ABC=74°,∠ACB=46°,∴∠BOE= 的度数为 的度数为
22. (1)证明:∵BC平分∠ABD,∴∠DBC=∠ABC,∴∠CAD=∠DBC,∴∠CAD=∠ABC.
(2)解:∵
∵AD是⊙O的直径,
23. 解:略
(2)由勾股定理得, 易求得AB所扫过的面积
24. 证明:(1)∵正方形ABCD内接于⊙O,∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°,又∵DF∥BE,∴∠EDF+∠BED=180°,∴∠EDF=90°,∴四边形 EBFD是矩形. (2)∵正方形ABCD 内接于⊙O,∴AD的度数是 90°,∴∠AFD=45°,又∵∠GDF=90°,∴∠DGF=∠DFG=45°,∴DG=DF,又∵在矩形EBFD中,BE=DF,∴BE=DG.
,
班级 学号 姓名 得分
一、选择题(本大题有10小题,每小题3分,共30分)
1.如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )
A. 70° B. 110° C. 130° D. 140°
2.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形
3. 如图,正五边形 ABCDE 内接于⊙O,P 为l 上的一点(点P不与点D重合),则∠CPD的度数为( )
A. 30° B. 36° C. 60° D. 72°
4. 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为E,∠AOB=90°,则阴影部分的面积是( )
A. 4π-4 B. 2π-4 C. 4π D. 2π
5. 如图,分别以等边三角形ABC的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若AB=2,则莱洛三角形的面积(即阴影部分面积)为( )
6. 如图,正六边形 ABCDEF 内接于半径为4 的圆O,则这个正六边形的边心距OM和弧BC的长分别为 ( )
A. 2,
7. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长为( )
A. 2π B. π C. D.
8. 如图,四边形ABCD内接于⊙O,F是CD上一点,且 连结CF 并延长交AD 的延长线于点E,连结AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A. 45° B. 50° C. 55° D. 60°
(解题指导)
9. 如图,四边形 ABCD 内接于⊙O,AE⊥CB交CB 的延长线于点E,若 BA 平分∠DBE,AD=5,CE 则AE等于( )
A. 3
10. 如图所示,一条公路的转弯处是一段圆弧(即图中点 O是 的圆心),其中 CD=600m,点E为CD上一点,且OE⊥CD,垂足为F, 则这段弯路的长度为( )
A. 200πm
B. 100πm
C. 400πm
D. 300πm
二、填空题(本大题有6小题,每小题4分,共24分)
11.若扇形的圆心角为45°,半径为3,则该扇形的弧长为 .
12. 如图,在平行四边形ABCD中,AB
14. 刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积.若用圆的内接正十二边形的面积S 来近似估计⊙O的面积S,设⊙O的半径为1,则
15. 如图,已知等边三角形ABC的边长为6,以AB为直径的⊙O与边AC,BC 分别交于D,E 两点,则劣弧. 的长为 .
16. 如图,四边形 ABCD 内接于⊙O,∠DAB=130°,连结OC.点 P 是半径OC 上任意一点,连结DP,BP,则∠BPD可能为 度(写出一个即可).
三、解答题(本大题有8小题,共66分)
17.(6分)已知扇形的圆心角为120°,弧长为20πcm,求扇形的面积.
18.(6分)如图所示,四边形 ABCD内接于⊙O,并且AD是⊙O的直径,C是BD的中点,AB 和DC 的延长线交于⊙O外一点E.求证:
19. (6分)如图,AB为⊙O的直径, 于点E,交⊙O于点C,D,( 于点 F.
(1)请写出三条与 BC有关的正确结论;
(2)当 时,求图中阴影部分的面积.
20.(8分)如图,点O是线段AB 的中点,根据要求完成下题:
(1)在图中完成下面的操作:
第一步,以AB为直径画出⊙O;
第二步,以B为圆心,以 BO为半径画圆弧,交⊙O于点C,连结CA,CO.
(2)设 ,求扇形 AOC的面积(结果保留π).
21.(8分)如图,⊙O是 的外接圆,BC的垂直平分线与 相交于D 点,若
求AD的度数.
22.(10分)如图,已知 是⊙O的内接三角形,AD 是⊙O的直径,连结 BD,BC平分
(1)求证:
(2)若 求 的长.
23.(10分)如图,在边长为1的正方形组成的网格中, 的顶点均在格点上,其中点 A(5,4), B(1,3),将 绕点O逆时针旋转 后得到
(1)画出
(2)求在旋转过程中线段AB扫过的图形的面积.
24.(12分)正方形 ABCD 内接于⊙O,如图所示,在劣弧AB上取一点 E,连结DE,BE,过点 D 作 交⊙O于点F,连结BF,AF,且AF与DE 相交于点G.
求证:(1)四边形EBFD是矩形;
第三章 圆的基本性质
1. B 2. A 3. B 4. D 5. D 6. D 7. B
8. B 9. D 10. A 11
14. π-3 15. π 16. 60(答案不唯一,大于或等于50且小于或等于100即可)
17. 解:设扇形的半径为 Rcm, ∴面积 ∴扇形面积为
18. 证明:如图,连结 AC.∵AD是⊙O的直径, ∠ACE.∵四边形 ABCD 内接于⊙O, 又∵ .∠EBC=∠D.∵C是 的中点,∴∠1=∠2,又∵ ∴∠E=∠D,∴∠EBC=∠E,∴BC=EC.
19. 解:(1)①BC=BD,②BC∥OF,③BC=2OF等(合理即可). (2)连结OC,∵OA=OC,∴∠A=∠ACO.∵∠A=∠D=30°,∠ACO=30°,AB=
20. 解:(1)如图. (2)如图,连结BC,则 BC=BO=OC,∴△BOC是等边三角形,∴∠BOC=60°,∴∠AOC=120°,∴S点形AOC =
21. 解:如图,连结OB,OC,AO,BC的垂直平分线必过点 O,设DO交 BC 于 点 E, ∴∠BOE = ∴∠BOE=∠BAC,∵∠ABC=74°,∠ACB=46°,∴∠BOE= 的度数为 的度数为
22. (1)证明:∵BC平分∠ABD,∴∠DBC=∠ABC,∴∠CAD=∠DBC,∴∠CAD=∠ABC.
(2)解:∵
∵AD是⊙O的直径,
23. 解:略
(2)由勾股定理得, 易求得AB所扫过的面积
24. 证明:(1)∵正方形ABCD内接于⊙O,∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°,又∵DF∥BE,∴∠EDF+∠BED=180°,∴∠EDF=90°,∴四边形 EBFD是矩形. (2)∵正方形ABCD 内接于⊙O,∴AD的度数是 90°,∴∠AFD=45°,又∵∠GDF=90°,∴∠DGF=∠DFG=45°,∴DG=DF,又∵在矩形EBFD中,BE=DF,∴BE=DG.
,
同课章节目录
