浙教版数学九年级上册 第3章测试卷 圆的基本性质(含答案)
文档属性
| 名称 | 浙教版数学九年级上册 第3章测试卷 圆的基本性质(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-14 22:04:40 | ||
图片预览

文档简介
第3章测试卷 圆的基本性质
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1.已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )
A. 一定在⊙O的内部 B. 一定在⊙O的外部
C. 一定在⊙O上 D. 不能确定
2.正六边形的每个内角度数为( )
A. 90° B. 108° C. 120° D. 150°
3.如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )
A. 60° B. 50° C. 40° D. 20°
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是( )
A B. C. 6 D. 8
5. 下列有关圆的一些结论:①与半径长相等的弦所对的圆周角是30°;②圆内接正六边形的边长与该圆半径相等;③垂直于弦的直径平分这条弦;④平分弦的直径垂直于弦.其中正确的是( )
A. ①②③ B. ①③④ C. ②③ D. ②④
6. 如图,正方形ABCD 内接于⊙O, 则 的长是( )
A. π C. 2π D
7.如图,已知 BC 是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点 A,点C重合),BD与OA交于点E,设∠AED=α,∠AOD=β,则( )
A. 3α+β=180° B. 2α+β=180° C. 3α-β=90° D. 2α-β=90°
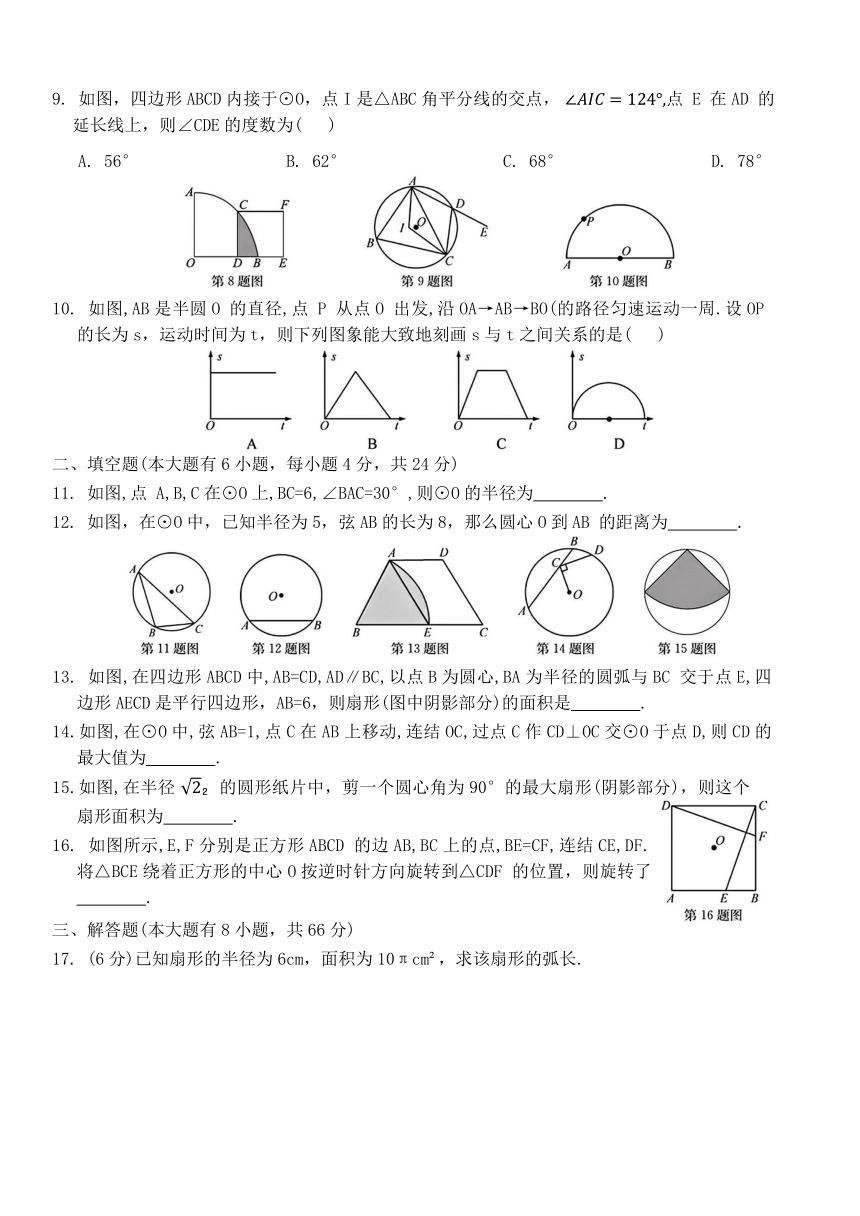
8. 如图,在扇形 AOB中,∠AOB=90°,点C 是弧AB 的中点,点 D 在OB 上,点 E 在OB 的延长线上,当正方形CDEF的边长为2时,则阴影部分的面积为( )
A. π-2 B. 2π—2 C. π—4 D. 2π-4
9. 如图,四边形ABCD内接于⊙O,点I是△ABC角平分线的交点, 点 E 在AD 的延长线上,则∠CDE的度数为( )
A. 56° B. 62° C. 68° D. 78°
10. 如图,AB是半圆O 的直径,点 P 从点O 出发,沿OA→AB→BO(的路径匀速运动一周.设OP 的长为s,运动时间为t,则下列图象能大致地刻画s与t之间关系的是( )
二、填空题(本大题有6小题,每小题4分,共24分)
11. 如图,点 A,B,C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为 .
12. 如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB 的距离为 .
13. 如图,在四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC 交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .
14.如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .
15.如图,在半径 的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形面积为 .
16. 如图所示,E,F分别是正方形ABCD 的边AB,BC上的点,BE=CF,连结CE,DF.将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF 的位置,则旋转了 .
三、解答题(本大题有8小题,共66分)
17. (6分)已知扇形的半径为6cm,面积为10πcm ,求该扇形的弧长.
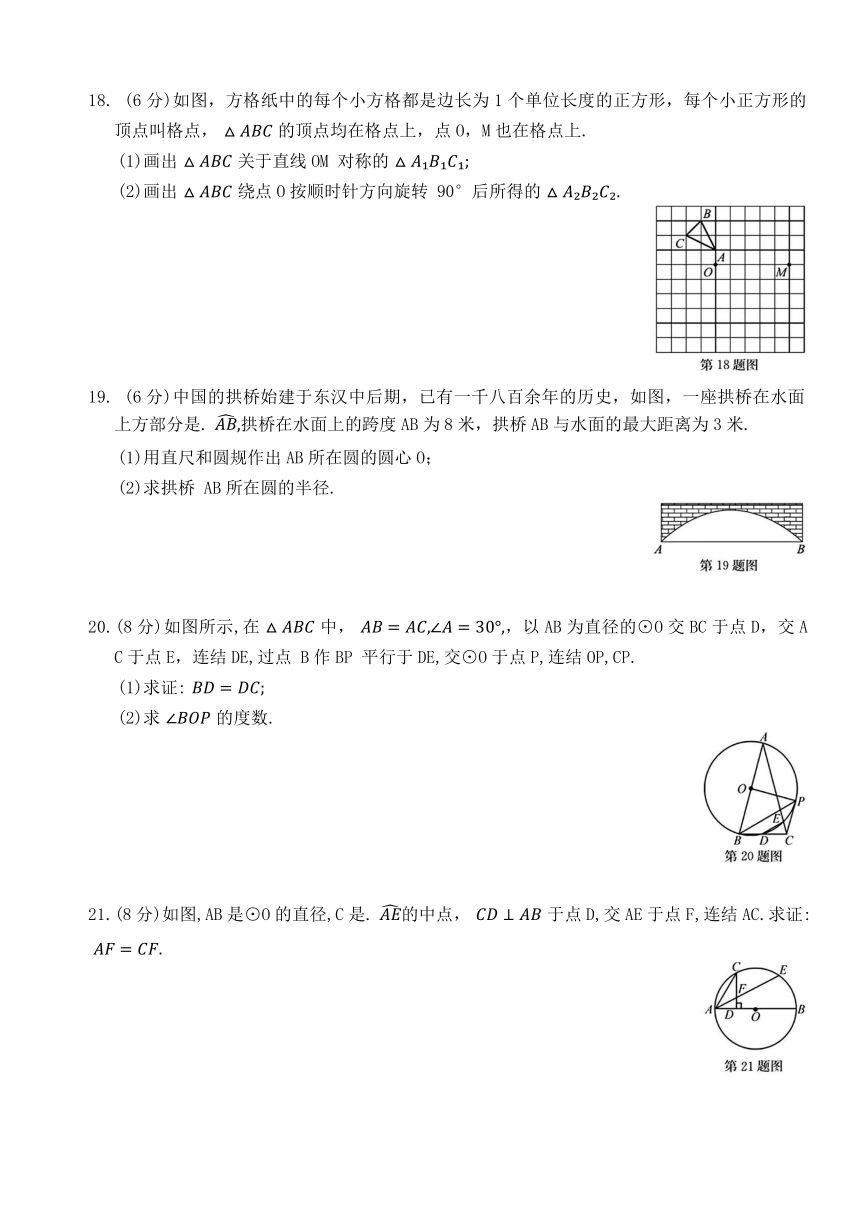
18. (6分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点, 的顶点均在格点上,点O,M也在格点上.
(1)画出 关于直线OM 对称的
(2)画出 绕点O按顺时针方向旋转 90°后所得的
19. (6分)中国的拱桥始建于东汉中后期,已有一千八百余年的历史,如图,一座拱桥在水面上方部分是. 拱桥在水面上的跨度AB为8米,拱桥AB与水面的最大距离为3米.
(1)用直尺和圆规作出AB所在圆的圆心O;
(2)求拱桥 AB所在圆的半径.
20.(8分)如图所示,在 中, ,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点 B作BP 平行于DE,交⊙O于点P,连结OP,CP.
(1)求证:
(2)求 的度数.
21.(8分)如图,AB是⊙O的直径,C是. 的中点, 于点D,交AE于点F,连结AC.求证:
22.(10分)如图,A,P,B,C是⊙O上的四点,且满足
(1) 试判断 是否为等边三角形 为什么
(2)若⊙O的半径 于点E, ,求⊙O的半径长.
23.(10分)如图,在 中, E在AC上,经过A,B,E三点的⊙O交BC 于点D,且.
(1)求证:AB为⊙O的直径;
(2)若 ,求阴影部分的面积.
24.(12分)如图,点A,B,C是⊙O上的三点,AB∥OC.
(1)求证:AC平分
(2)如图,过点O作( 于点E,交AC于点 P.若AB=2,∠AOE=30°,求 PE的长.
第3章测试卷 圆的基本性质
1. B 2. C 3. B 4. B 5. C 6. A 7. D8. A 9. C 10. C 11. 6 12. 3 13. 6π14 15. π 16. 90
17. 解:由 得
18. 解:(1)如图, 即为所求作的三角形.
(2)如图, 即为所求作的三角形.
19. 解:(1)如图1所示,点 O即为所求;
(2)如图2 所示,取 的中点D,连结OD交AB 于点 E,连结OA,则 且AE=EB=4米,
由题意得,DE=3米,设圆的半径为r米,在 Rt△AEO中, 即 解得 即拱桥AB所在圆的半径为 米.
20. (1)证明:如图,连结 AD.∵AB为⊙O的直径,∴∠ADB=90°,即 AD⊥BC,∵AB=AC,∴BD=CD. (2)解:∵∠BAC= 30°,AB= AC,∴ 75°.∵四边形 ABDE 为圆O 的内接四边形,∴∠EDC=∠BAC=30°.∵BP∥DE,∴∠PBC=∠EDC=30°,∴∠OBP=∠ABC--∠PBC=45°.∵OB=OP,∴∠OPB=∠OBP=45°,∴∠BOP
21. 证明:延长CD 交⊙O 于点 H,∵C是 的中点, ∴∠ACD=∠CAE,∴AF=CF.
22. 解:(1)△ABC 是等边三角形.理由:∵∠BAC=∠APC=60°,又∵∠APC=∠ABC,∴∠ABC= 是等边三角形. (2)如图,连结OB,∵△ABC为等边三角形,⊙O为其外接圆,∴BO平分∠ABC,∴∠OBC=30°,∵OD ∴OO|的半径长
23. (1)证明:如图,连结.AD, 又∵AB = AC, ∴AD ⊥ BC, ∴∠ADB=90°,∴AB 为⊙O的直径. (2)解:∵AB为⊙O的直径,∴O在AB上,如图,连结OE,∵AB=8,∠BAC=45°,∴∠AOE=∠BOE=
24. (1)证明:∵AB∥OC,∴∠C=∠BAC.∵OA=OC,∴∠C=∠OAC,∴∠BAC=∠OAC,即AC平分∠OAB. (2)解: =1,又∵∠AOE 、30°,∠PEA=90°,∴∠OAE= 设PE=x,则 PA=2x,根据勾股定理得 (2x) ,解得
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1.已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )
A. 一定在⊙O的内部 B. 一定在⊙O的外部
C. 一定在⊙O上 D. 不能确定
2.正六边形的每个内角度数为( )
A. 90° B. 108° C. 120° D. 150°
3.如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )
A. 60° B. 50° C. 40° D. 20°
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是( )
A B. C. 6 D. 8
5. 下列有关圆的一些结论:①与半径长相等的弦所对的圆周角是30°;②圆内接正六边形的边长与该圆半径相等;③垂直于弦的直径平分这条弦;④平分弦的直径垂直于弦.其中正确的是( )
A. ①②③ B. ①③④ C. ②③ D. ②④
6. 如图,正方形ABCD 内接于⊙O, 则 的长是( )
A. π C. 2π D
7.如图,已知 BC 是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点 A,点C重合),BD与OA交于点E,设∠AED=α,∠AOD=β,则( )
A. 3α+β=180° B. 2α+β=180° C. 3α-β=90° D. 2α-β=90°
8. 如图,在扇形 AOB中,∠AOB=90°,点C 是弧AB 的中点,点 D 在OB 上,点 E 在OB 的延长线上,当正方形CDEF的边长为2时,则阴影部分的面积为( )
A. π-2 B. 2π—2 C. π—4 D. 2π-4
9. 如图,四边形ABCD内接于⊙O,点I是△ABC角平分线的交点, 点 E 在AD 的延长线上,则∠CDE的度数为( )
A. 56° B. 62° C. 68° D. 78°
10. 如图,AB是半圆O 的直径,点 P 从点O 出发,沿OA→AB→BO(的路径匀速运动一周.设OP 的长为s,运动时间为t,则下列图象能大致地刻画s与t之间关系的是( )
二、填空题(本大题有6小题,每小题4分,共24分)
11. 如图,点 A,B,C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为 .
12. 如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB 的距离为 .
13. 如图,在四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC 交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .
14.如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .
15.如图,在半径 的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形面积为 .
16. 如图所示,E,F分别是正方形ABCD 的边AB,BC上的点,BE=CF,连结CE,DF.将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF 的位置,则旋转了 .
三、解答题(本大题有8小题,共66分)
17. (6分)已知扇形的半径为6cm,面积为10πcm ,求该扇形的弧长.
18. (6分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点, 的顶点均在格点上,点O,M也在格点上.
(1)画出 关于直线OM 对称的
(2)画出 绕点O按顺时针方向旋转 90°后所得的
19. (6分)中国的拱桥始建于东汉中后期,已有一千八百余年的历史,如图,一座拱桥在水面上方部分是. 拱桥在水面上的跨度AB为8米,拱桥AB与水面的最大距离为3米.
(1)用直尺和圆规作出AB所在圆的圆心O;
(2)求拱桥 AB所在圆的半径.
20.(8分)如图所示,在 中, ,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点 B作BP 平行于DE,交⊙O于点P,连结OP,CP.
(1)求证:
(2)求 的度数.
21.(8分)如图,AB是⊙O的直径,C是. 的中点, 于点D,交AE于点F,连结AC.求证:
22.(10分)如图,A,P,B,C是⊙O上的四点,且满足
(1) 试判断 是否为等边三角形 为什么
(2)若⊙O的半径 于点E, ,求⊙O的半径长.
23.(10分)如图,在 中, E在AC上,经过A,B,E三点的⊙O交BC 于点D,且.
(1)求证:AB为⊙O的直径;
(2)若 ,求阴影部分的面积.
24.(12分)如图,点A,B,C是⊙O上的三点,AB∥OC.
(1)求证:AC平分
(2)如图,过点O作( 于点E,交AC于点 P.若AB=2,∠AOE=30°,求 PE的长.
第3章测试卷 圆的基本性质
1. B 2. C 3. B 4. B 5. C 6. A 7. D8. A 9. C 10. C 11. 6 12. 3 13. 6π14 15. π 16. 90
17. 解:由 得
18. 解:(1)如图, 即为所求作的三角形.
(2)如图, 即为所求作的三角形.
19. 解:(1)如图1所示,点 O即为所求;
(2)如图2 所示,取 的中点D,连结OD交AB 于点 E,连结OA,则 且AE=EB=4米,
由题意得,DE=3米,设圆的半径为r米,在 Rt△AEO中, 即 解得 即拱桥AB所在圆的半径为 米.
20. (1)证明:如图,连结 AD.∵AB为⊙O的直径,∴∠ADB=90°,即 AD⊥BC,∵AB=AC,∴BD=CD. (2)解:∵∠BAC= 30°,AB= AC,∴ 75°.∵四边形 ABDE 为圆O 的内接四边形,∴∠EDC=∠BAC=30°.∵BP∥DE,∴∠PBC=∠EDC=30°,∴∠OBP=∠ABC--∠PBC=45°.∵OB=OP,∴∠OPB=∠OBP=45°,∴∠BOP
21. 证明:延长CD 交⊙O 于点 H,∵C是 的中点, ∴∠ACD=∠CAE,∴AF=CF.
22. 解:(1)△ABC 是等边三角形.理由:∵∠BAC=∠APC=60°,又∵∠APC=∠ABC,∴∠ABC= 是等边三角形. (2)如图,连结OB,∵△ABC为等边三角形,⊙O为其外接圆,∴BO平分∠ABC,∴∠OBC=30°,∵OD ∴OO|的半径长
23. (1)证明:如图,连结.AD, 又∵AB = AC, ∴AD ⊥ BC, ∴∠ADB=90°,∴AB 为⊙O的直径. (2)解:∵AB为⊙O的直径,∴O在AB上,如图,连结OE,∵AB=8,∠BAC=45°,∴∠AOE=∠BOE=
24. (1)证明:∵AB∥OC,∴∠C=∠BAC.∵OA=OC,∴∠C=∠OAC,∴∠BAC=∠OAC,即AC平分∠OAB. (2)解: =1,又∵∠AOE 、30°,∠PEA=90°,∴∠OAE= 设PE=x,则 PA=2x,根据勾股定理得 (2x) ,解得
同课章节目录
