浙教版数学九年级下册 第1章 解直角三角形(含答案)
文档属性
| 名称 | 浙教版数学九年级下册 第1章 解直角三角形(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-16 00:00:00 | ||
图片预览


文档简介
第1章 解直角三角形
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1. 在 Rt△ABC中, 那么sinA的值是( )
D
2.如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A. c=bsinB B. b=csinB C. a=btanB D. b=ctanB
3. 如图,有一斜坡AB,坡顶B离地面的高度BC 为30m,斜坡的倾斜角是∠BAC,若 则此斜坡的水平距离AC为( )
A. 75m B. 50m C. 30m D. 12m
4. 如图,电线杆CD 的高度为h,两根拉线AC与BC 相互垂直,∠CAB=α,则拉线 BC的长度为(A,D,B在同一条直线上)( )
D. h·cosα
5.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
A C. 2
6. 如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD的值是( )
A B C D. 2
7.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A'B'的位置,已知AO的长为4米.若栏杆的旋转角. 则栏杆A端升高的高度为( )
米 B. 4sinα米 米 D. 4cosα米
8. 南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A 测得大桥主架与水面的交汇点C 的俯角为α,大桥主架的顶端D 的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A. asinα+asinβ B. acosα+acosβ C. atanα+atanβ
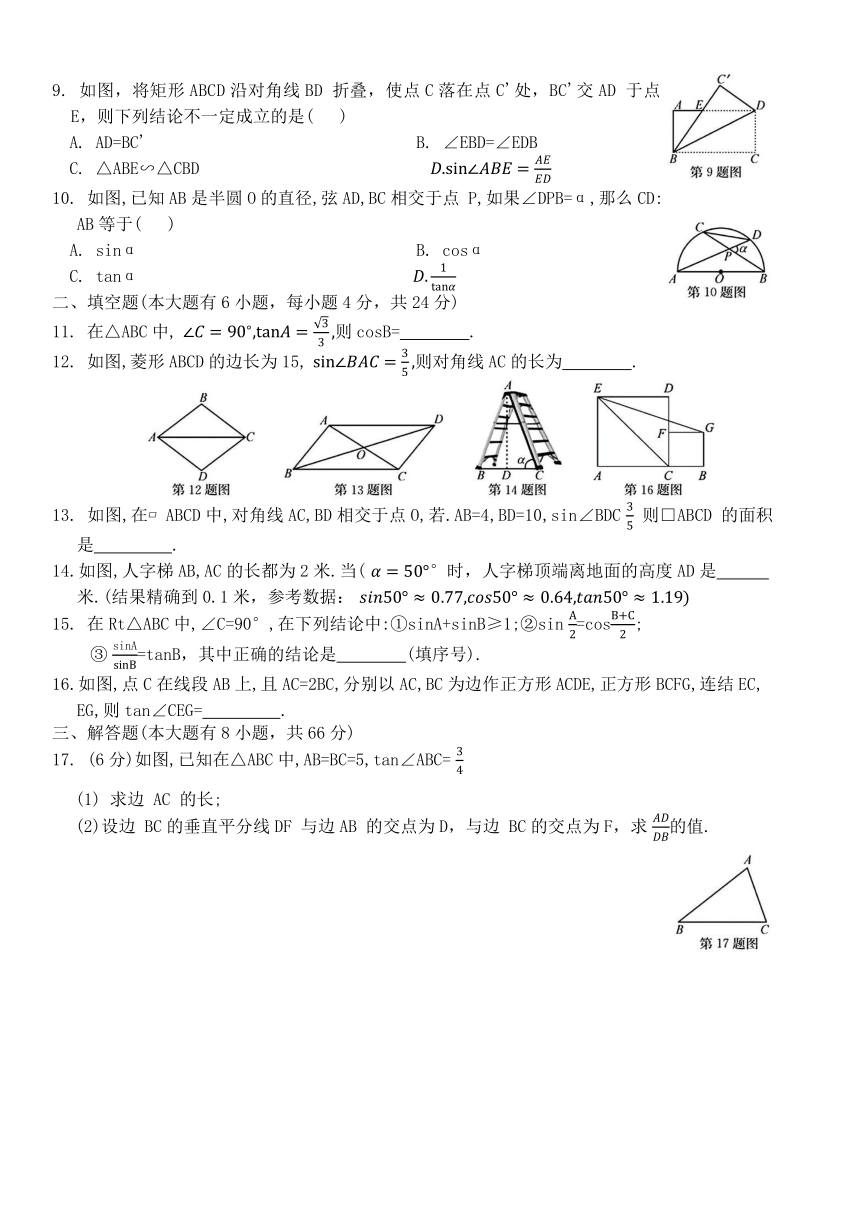
9. 如图,将矩形ABCD沿对角线BD 折叠,使点C落在点C'处,BC'交AD 于点E,则下列结论不一定成立的是( )
A. AD=BC' B. ∠EBD=∠EDB
C. △ABE∽△CBD
10. 如图,已知AB是半圆O的直径,弦AD,BC相交于点 P,如果∠DPB=α,那么CD:AB等于( )
A. sinα B. cosα
C. tanα
二、填空题(本大题有6小题,每小题4分,共24分)
11. 在△ABC中, 则cosB= .
12. 如图,菱形ABCD的边长为15, 则对角线AC的长为 .
13. 如图,在 ABCD中,对角线AC,BD相交于点O,若.AB=4,BD=10,sin∠BDC 则□ABCD 的面积是 .
14.如图,人字梯AB,AC的长都为2米.当( °时,人字梯顶端离地面的高度AD是 米.(结果精确到0.1米,参考数据:
15. 在Rt△ABC中,∠C=90°,在下列结论中:①sinA+sinB≥1;②sin =cos;
③ =tanB,其中正确的结论是 (填序号).
16.如图,点C在线段AB上,且AC=2BC,分别以AC,BC为边作正方形ACDE,正方形BCFG,连结EC, EG,则tan∠CEG= .
三、解答题(本大题有8小题,共66分)
17. (6分)如图,已知在△ABC中,AB=BC=5,tan∠ABC=
(1) 求边 AC 的长;
(2)设边 BC的垂直平分线DF 与边AB 的交点为D,与边 BC的交点为F,求 的值.
18. (6分)计算:
19.(6分)如图,已知△ABC.按如下步骤作图:①以A 为圆心,AB长为半径画弧;②以C为圆心, CB 长为半径画弧,两弧相交于点 D;③连结BD,与AC交于点E,连结AD,CD.
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.
20.(8分)如图,在△ABC中,已知AD是BC 边上的高,AE是BC 边上的中线,且
(1)用含α的式子分别表示AD 和△ABC的面积S;
(2)用含α的式子表示 tan∠DAE.
21.(8分)图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2 是其示意图,经测量,钢条AB=AC=50cm,∠ABC=47°.
(1)求车位锁的底盒长 BC.
(2)若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位 (参考数据: 0.73,cos47°≈0.68,tan47°≈1.07)
22.(10分)如图,已知锐角三角形ABC的外接圆圆心为O,半径为R.
(1)求证:
(2)若 中 求BC的长及 sinC的值.
23.(10分)关于x的方程 有两个相等的实数根,其中 是锐角三角形ABC的一个内角.
(1)求 sinA 的值;
(2)若关于y的方程 的两个根恰好是 的两边长,求 的周长.
24.(12分)如图,某巡逻艇计划以40海里/时的速度从A 处向正东方向的D 处航行,出发 1.5小时到达 B处时,突然接到C处的求救信号,于是巡逻艇立刻以 60海里/时的速度向北偏东 方向的C处航行,到达C处后,测得A处位于C 处的南偏西( 方向,解救后巡逻艇又沿南偏东 方向航行到 D 处.
(1)求巡逻艇从B处到C处用的时间;
(2)求巡逻艇实际比原计划多航行多少海里(结果精确到1海里,参考数据:
第1章 解直角三角形
1. B 2. B 3. A 4. B 5. A 6. C 7. B 8. C9. C
10. B 解析:如图,连结BD,由AB 是直径得 ∴△CPD∽△APB,∴CD: AB=PD:PB=cosα.
12. 24 13. 24 14. 1.5 15.② 16
17. 解:(1)如图,过点 A 作. BC,在 Rt△ABE中,tan∠ABC BE=4,∴CE=BC--BE=5-4=1,在Rt△AEC中,根据勾股定理得:
(2)如图,连结CD,∵DF垂直平分BC,∴BD=CD,BF=CF=
在Rt△BFD 中, 根 据 勾 股 定 理 得: BD =
则
18. 解: +1=1.
(2)原式
19. (1)证明:在△ABC 与△ADC 中, △ABC≌△ADC(SSS). (2)解:设 BE=x,∵
20. 解:(1)∵AD 是 BC 边上的高,∴AD=ABsinα= (2)∵E是BC的中点,∴EC=4,又∵∠C=45°,
∴DC=AD=5sing,ED=EC--DC=4-5sina, (或化简为
21. 解:(1)如图,过点A作AH⊥BC 于点 H,∵AB=AC,∴BH= HC,在 Rt△ABH 中,∠B=47°,AB=50,∴BH= 0.68=34,∴BC=2BH≈68cm.
(2)在 Rt△ABH中, (cm),∵36.5>30,
∴当车位锁上锁时,这辆汽车不能进入该车位.
(1)证明:如图,连结 AO并延长交⊙O于点D,连结CD,则∠ACD=90°,∠ABC=∠ADC,∴sin∠ABC= 2R.
解: 同理可得:
如图,过C作CE⊥AB于点E,∴BE=BC·cosB
解:(1)因为关于x的方程有两个相等的实数根,则 ∵∠A为锐角,
(2)由题意知,方程 有两个实数根,则△≥0,
(k-2) ≤0,又∵(k-2) ≥0,∴k=2.把k=2代入方程,得 解得 是等腰三角形,且腰长为5.分两种情况:
①∠A 是顶角时:如图1,过点 B作 于点D,在Rt△ABD中,
3,BD=4,∴DC=2,∴BC= .∴△ABC的周为10+
②∠A 是底角时:如图2,过点 B 作BD⊥AC于点D,在 Rt△ABD中,AB=5,∵sinA= ,
∴AD=DC=3,∴AC=6.∴△AB 的周长为16.综上可知:△ABC的周长为 或16.
24. 解:(1)如图,过点 C作CE⊥AD,垂足为E,AB=40×1.5=60'海里),由题意知:∠BCE=30°,
∠ACE=60°,∴∠ACB=∠ACE--∠BCE=30°,由∠AEC=90°,∠ACE=60°,知∠A=30°,∴∠A=∠ACB,BC=AB=60海里,∴船从B处到C 处用的时间为:60÷60=1(小时). (2)由 BC=60海里,∠BCE=30°得( 海里,BE=30海里,又∠ECD=45°,∴ED=EC=3 海里,CD= 海里,∴船多航行的路程为:实际航行路程一原航行路程=(AB+BC+CD)-(AB 1.73≈52(海里).答:巡逻艇实际比原计划多航行52海里.
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1. 在 Rt△ABC中, 那么sinA的值是( )
D
2.如图,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
A. c=bsinB B. b=csinB C. a=btanB D. b=ctanB
3. 如图,有一斜坡AB,坡顶B离地面的高度BC 为30m,斜坡的倾斜角是∠BAC,若 则此斜坡的水平距离AC为( )
A. 75m B. 50m C. 30m D. 12m
4. 如图,电线杆CD 的高度为h,两根拉线AC与BC 相互垂直,∠CAB=α,则拉线 BC的长度为(A,D,B在同一条直线上)( )
D. h·cosα
5.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为( )
A C. 2
6. 如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD的值是( )
A B C D. 2
7.如图,某停车场入口的栏杆AB,从水平位置绕点O旋转到A'B'的位置,已知AO的长为4米.若栏杆的旋转角. 则栏杆A端升高的高度为( )
米 B. 4sinα米 米 D. 4cosα米
8. 南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A 测得大桥主架与水面的交汇点C 的俯角为α,大桥主架的顶端D 的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A. asinα+asinβ B. acosα+acosβ C. atanα+atanβ
9. 如图,将矩形ABCD沿对角线BD 折叠,使点C落在点C'处,BC'交AD 于点E,则下列结论不一定成立的是( )
A. AD=BC' B. ∠EBD=∠EDB
C. △ABE∽△CBD
10. 如图,已知AB是半圆O的直径,弦AD,BC相交于点 P,如果∠DPB=α,那么CD:AB等于( )
A. sinα B. cosα
C. tanα
二、填空题(本大题有6小题,每小题4分,共24分)
11. 在△ABC中, 则cosB= .
12. 如图,菱形ABCD的边长为15, 则对角线AC的长为 .
13. 如图,在 ABCD中,对角线AC,BD相交于点O,若.AB=4,BD=10,sin∠BDC 则□ABCD 的面积是 .
14.如图,人字梯AB,AC的长都为2米.当( °时,人字梯顶端离地面的高度AD是 米.(结果精确到0.1米,参考数据:
15. 在Rt△ABC中,∠C=90°,在下列结论中:①sinA+sinB≥1;②sin =cos;
③ =tanB,其中正确的结论是 (填序号).
16.如图,点C在线段AB上,且AC=2BC,分别以AC,BC为边作正方形ACDE,正方形BCFG,连结EC, EG,则tan∠CEG= .
三、解答题(本大题有8小题,共66分)
17. (6分)如图,已知在△ABC中,AB=BC=5,tan∠ABC=
(1) 求边 AC 的长;
(2)设边 BC的垂直平分线DF 与边AB 的交点为D,与边 BC的交点为F,求 的值.
18. (6分)计算:
19.(6分)如图,已知△ABC.按如下步骤作图:①以A 为圆心,AB长为半径画弧;②以C为圆心, CB 长为半径画弧,两弧相交于点 D;③连结BD,与AC交于点E,连结AD,CD.
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.
20.(8分)如图,在△ABC中,已知AD是BC 边上的高,AE是BC 边上的中线,且
(1)用含α的式子分别表示AD 和△ABC的面积S;
(2)用含α的式子表示 tan∠DAE.
21.(8分)图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2 是其示意图,经测量,钢条AB=AC=50cm,∠ABC=47°.
(1)求车位锁的底盒长 BC.
(2)若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位 (参考数据: 0.73,cos47°≈0.68,tan47°≈1.07)
22.(10分)如图,已知锐角三角形ABC的外接圆圆心为O,半径为R.
(1)求证:
(2)若 中 求BC的长及 sinC的值.
23.(10分)关于x的方程 有两个相等的实数根,其中 是锐角三角形ABC的一个内角.
(1)求 sinA 的值;
(2)若关于y的方程 的两个根恰好是 的两边长,求 的周长.
24.(12分)如图,某巡逻艇计划以40海里/时的速度从A 处向正东方向的D 处航行,出发 1.5小时到达 B处时,突然接到C处的求救信号,于是巡逻艇立刻以 60海里/时的速度向北偏东 方向的C处航行,到达C处后,测得A处位于C 处的南偏西( 方向,解救后巡逻艇又沿南偏东 方向航行到 D 处.
(1)求巡逻艇从B处到C处用的时间;
(2)求巡逻艇实际比原计划多航行多少海里(结果精确到1海里,参考数据:
第1章 解直角三角形
1. B 2. B 3. A 4. B 5. A 6. C 7. B 8. C9. C
10. B 解析:如图,连结BD,由AB 是直径得 ∴△CPD∽△APB,∴CD: AB=PD:PB=cosα.
12. 24 13. 24 14. 1.5 15.② 16
17. 解:(1)如图,过点 A 作. BC,在 Rt△ABE中,tan∠ABC BE=4,∴CE=BC--BE=5-4=1,在Rt△AEC中,根据勾股定理得:
(2)如图,连结CD,∵DF垂直平分BC,∴BD=CD,BF=CF=
在Rt△BFD 中, 根 据 勾 股 定 理 得: BD =
则
18. 解: +1=1.
(2)原式
19. (1)证明:在△ABC 与△ADC 中, △ABC≌△ADC(SSS). (2)解:设 BE=x,∵
20. 解:(1)∵AD 是 BC 边上的高,∴AD=ABsinα= (2)∵E是BC的中点,∴EC=4,又∵∠C=45°,
∴DC=AD=5sing,ED=EC--DC=4-5sina, (或化简为
21. 解:(1)如图,过点A作AH⊥BC 于点 H,∵AB=AC,∴BH= HC,在 Rt△ABH 中,∠B=47°,AB=50,∴BH= 0.68=34,∴BC=2BH≈68cm.
(2)在 Rt△ABH中, (cm),∵36.5>30,
∴当车位锁上锁时,这辆汽车不能进入该车位.
(1)证明:如图,连结 AO并延长交⊙O于点D,连结CD,则∠ACD=90°,∠ABC=∠ADC,∴sin∠ABC= 2R.
解: 同理可得:
如图,过C作CE⊥AB于点E,∴BE=BC·cosB
解:(1)因为关于x的方程有两个相等的实数根,则 ∵∠A为锐角,
(2)由题意知,方程 有两个实数根,则△≥0,
(k-2) ≤0,又∵(k-2) ≥0,∴k=2.把k=2代入方程,得 解得 是等腰三角形,且腰长为5.分两种情况:
①∠A 是顶角时:如图1,过点 B作 于点D,在Rt△ABD中,
3,BD=4,∴DC=2,∴BC= .∴△ABC的周为10+
②∠A 是底角时:如图2,过点 B 作BD⊥AC于点D,在 Rt△ABD中,AB=5,∵sinA= ,
∴AD=DC=3,∴AC=6.∴△AB 的周长为16.综上可知:△ABC的周长为 或16.
24. 解:(1)如图,过点 C作CE⊥AD,垂足为E,AB=40×1.5=60'海里),由题意知:∠BCE=30°,
∠ACE=60°,∴∠ACB=∠ACE--∠BCE=30°,由∠AEC=90°,∠ACE=60°,知∠A=30°,∴∠A=∠ACB,BC=AB=60海里,∴船从B处到C 处用的时间为:60÷60=1(小时). (2)由 BC=60海里,∠BCE=30°得( 海里,BE=30海里,又∠ECD=45°,∴ED=EC=3 海里,CD= 海里,∴船多航行的路程为:实际航行路程一原航行路程=(AB+BC+CD)-(AB 1.73≈52(海里).答:巡逻艇实际比原计划多航行52海里.
