浙教版数学九年级下册 第2章 直线与圆的位置关系(含答案)
文档属性
| 名称 | 浙教版数学九年级下册 第2章 直线与圆的位置关系(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-16 07:06:06 | ||
图片预览


文档简介
第2章 直线与圆的位置关系
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A. 三条边的垂直平分线的交点 B. 三个内角平分线的交点
C. 三条中线的交点 D. 三条高的交点
2. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA 交小圆于点D,若 OD=2,tan∠OAB= ,则AB的长是( )
A. 4 C. 8
3.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA 交OC 的延长线于点P,则PA的长为( )
A. 2 B. C D
4.如图,菱形OABC的顶点A,B,C在⊙O上,过点 B作⊙O的切线交OA 的延长线于点D.若⊙O的半径为1,则BD的长为( )
A. 1 B. 2 C
5.如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
A. DC=DT C. BD=BO D. 2OC=5AC
6.若正方形的外接圆半径为2,则其内切圆半径为( )
A D. 1
7.如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
A. 2 C. 1
8. 如图,过⊙O外一点P 引⊙O的两条切线PA,PB,切点分别是A,B,OP 交⊙O于点C,点 D是优弧 上不与点A,C重合的一个动点,连结AD,CD,若∠APB=80°,则∠ADC的度数是( )
A. 15° B. 20° C. 25° D. 30°
9. 如图,一把直尺、一块含60°角的直角三角板和一张光盘如图摆放,60°角的顶点 A 在直尺上,AB=3,则光盘的直径是( )
A. 3 D
10. 在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P 在直线. 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为( )
A. 3 B. 2 C D
二、填空题(本大题有6小题,每小题4分,共24分)
11. 在平面直角坐标系内,圆心A的坐标是(3,-5),如果⊙A经过点(0,-1),那么⊙A与x 轴的位置关系是
12.如图,在△ABC中,D是边BC 上的一点,以AD 为直径的⊙O交AC 于点E,连结DE.若⊙O与BC相切,∠ADE=55°,则∠C的度数为 .
13. 如图,∠ACB=60°,半径为1cm的⊙O切BC 于点C,若将⊙O在CB 上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是 cm.
14. 如图,PA,PB是⊙O的切线,A,B为切点,点 C,D在⊙O上.若∠P=102°,则∠A+∠C= .
15. 如图,AB为半圆O的直径,C为半圆弧的三等分点,过B,C两点的半圆O 的切线交于点P,若AB的长是2a,则 PA的长是 .
16. 如图,在矩形 ABCD中,AB=4,AD=3,以点C为圆心作⊙C 与直线BD 相切,点P 是⊙C 上一个动点,连结AP交BD 于点T,则 的最大值是 .
三、解答题(本大题有8小题,共66分)
17.(6分)已知:如图,在△OAB中,OA=OB,⊙O与AB 相切于点C.求证:AC=BC.小明同学的证明过程如下框:
证明:连结OC,
∵OA=OB,
∴∠A=∠B,
又∵OC=OC,
∴△OAC≌△OBC,
∴AC=BC.
小明的证法是否正确 若正确,请在框内打“ ”;若错误,请写出你的证明过程.
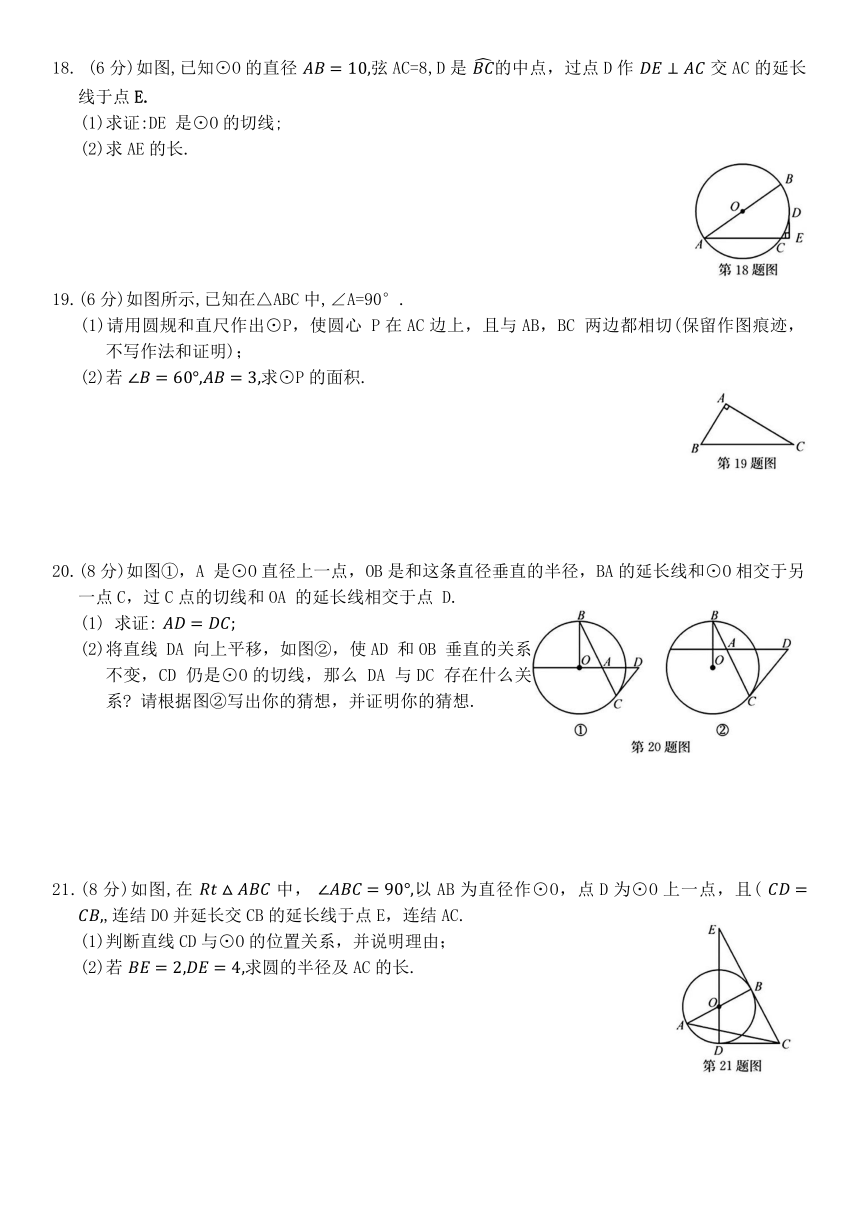
18. (6分)如图,已知⊙O的直径 弦AC=8,D是 的中点,过点D作 交AC的延长线于点E.
(1)求证:DE 是⊙O的切线;
(2)求AE的长.
19.(6分)如图所示,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心 P在AC边上,且与AB,BC 两边都相切(保留作图痕迹,不写作法和证明);
(2)若 求⊙P的面积.
20.(8分)如图①,A 是⊙O直径上一点,OB是和这条直径垂直的半径,BA的延长线和⊙O相交于另一点C,过C点的切线和OA 的延长线相交于点 D.
(1) 求证:
(2)将直线 DA 向上平移,如图②,使AD 和OB 垂直的关系不变,CD 仍是⊙O的切线,那么 DA 与DC 存在什么关系 请根据图②写出你的猜想,并证明你的猜想.
21.(8分)如图,在 中, 以AB为直径作⊙O,点D为⊙O上一点,且( ,连结DO并延长交CB的延长线于点E,连结AC.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若 求圆的半径及AC的长.
22.(10分)如图,AD是⊙O的直径,AB为⊙O的弦, ,OP 与AB 的延长线交于点 P,过B点的⊙O的切线交OP 于点C,连结BD.
(1)求证:
(2)若 求线段 BP 的长.
23.(10分)如图,点 A,B,C在半径为8的⊙O上,过点 B 作. ,交OA 延长线于点 D.连结 BC,且
(1)求证:BD是⊙O的切线;
(2)求图中阴影部分的面积.
24.(12分)如图,AB是⊙O的直径,点 D在AB 的延长线上,C,E是⊙O上的两点, 延长AE交BC的延长线于点 F.
(1)求证:CD是⊙O的切线;
(2)求证:
(3)若 求弦 AC的长.
第2章 直线与圆的位置关系
1. B 2. C 3. B 4. D 5. D 6. A7.C 8. C 9. C
10. D 解析:如图,设直线 与x轴交于点C,与y轴交于点D,作OH⊥CD于点H,当x=0时, 则 当y=0时 解得x=-2,则 C(-2,0),∴ 连 结 OP,OA,如图,∵PA为⊙O 的切线,∴ OA ⊥ PA, ∴ PA = 当OP 的值最小时,PA 的值最小,而OP 的最小值为OH 的长,∴PA的最小值为
11. 相切12. 55° 13. 14. 219
15. 16. 3
17. 解:证法错误.证明:连结OC,∵⊙O与AB 相切于点C,∴OC⊥AB,又∵OA=OB,∴AC=BC.
18. (1)证明:如图,连结OD,∵D是 的中点, =DC,∴∠BOD=∠BAE,∴OD∥AE,∵DE⊥AC,∴∠AED=90°,∴∠ODE=90°.∴OD⊥DE,∴DE是⊙O的切线C
(2)解:如图,过点 O作OF⊥AC 于点 F, 四边形OFED 是矩形, =10,∴FE=5,∴AE=AF+FE=5+4=9.
19. 解:(1)如图所示,则⊙P 即为所求作的圆.
(2)∵∠ABC=60°,BP 平分∠ABC,∴∠ABP= ∴S⊙P=3π.
20. (1)证明:连结OC,∵CD是切线,∴∠OCD=90°,∴∠DCA+∠OCB=90°.∵OB⊥OA,
∴∠OAB+∠B=90°,∵∠B=∠OCB,∴∠OAB=∠DCA.∵∠OAB=∠DAC,∴∠DAC=∠DCA,∴DA=DC.
(2)解:DC=DA.证明同上.
21. 解:(1)CD 与⊙O 相切.理由:连结OC.∵CB=CD,CO= CO,OB = OD,∴△OCB≌△OCD(SSS),∴∠ODC=∠OBC=90°,∴OD⊥DC,∴DC是⊙O的切线. (2)设⊙O的半径为r.在 Rt△OBE中, CD=BC=3,在 Rt△ABC中, 圆的半径为 1.5,AC 的长为
22. (1)证明:连结OB,如图,∵AD是⊙O的直径,∴∠ABD=90°,∴∠A+∠ADB=90°,∵BC 为切线,∴OB⊥BC,∴∠OBC= 而OA = OB, ∴∠A = ∠OBA,∴∠CBP=∠ADB. (2)解:∵ 即
23. (1)证明:连结OB,交 CA于点E,∵∠C=30°,∠C 即OB⊥AC,∵BD∥ AC, ∴∠DBE =∠AEO= 90°,∴BD 是⊙O的切线. (2)解: ∴∠D=∠OAC=30°,∵∠OBD=90°,OB=8,∴
24. (1)证明:如图,连结OC,∵AB是⊙O 的直径,∴∠ACB=90°,∴∠CAD+∠ABC=90°, ∠CAE=∠CAB,∵∠BCD=∠CAE,∴∠CAB=∠BCD,∵OB = OC, ∴∠OBC = ∠OCB, ∴∠OCB +∠BCD=90°,∴∠OCD=90°,∴CD是⊙O的切线.
(2)证明:∵∠BAC =∠CAE,∠ACB =∠ACF = 90°, AC = AC, ∴△ABC≌△AFC(ASA),∴CB=CF,又∵CB=CE,∴CE=CF.
(3)解:∵∠BCD=∠CAD,∠ADC=∠CDB,∴ 2,∴AB=AD-BD=2-1=1,设BC=a,AC a由勾股定理可得: 解得:
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A. 三条边的垂直平分线的交点 B. 三个内角平分线的交点
C. 三条中线的交点 D. 三条高的交点
2. 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,OA 交小圆于点D,若 OD=2,tan∠OAB= ,则AB的长是( )
A. 4 C. 8
3.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA 交OC 的延长线于点P,则PA的长为( )
A. 2 B. C D
4.如图,菱形OABC的顶点A,B,C在⊙O上,过点 B作⊙O的切线交OA 的延长线于点D.若⊙O的半径为1,则BD的长为( )
A. 1 B. 2 C
5.如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
A. DC=DT C. BD=BO D. 2OC=5AC
6.若正方形的外接圆半径为2,则其内切圆半径为( )
A D. 1
7.如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
A. 2 C. 1
8. 如图,过⊙O外一点P 引⊙O的两条切线PA,PB,切点分别是A,B,OP 交⊙O于点C,点 D是优弧 上不与点A,C重合的一个动点,连结AD,CD,若∠APB=80°,则∠ADC的度数是( )
A. 15° B. 20° C. 25° D. 30°
9. 如图,一把直尺、一块含60°角的直角三角板和一张光盘如图摆放,60°角的顶点 A 在直尺上,AB=3,则光盘的直径是( )
A. 3 D
10. 在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P 在直线. 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为( )
A. 3 B. 2 C D
二、填空题(本大题有6小题,每小题4分,共24分)
11. 在平面直角坐标系内,圆心A的坐标是(3,-5),如果⊙A经过点(0,-1),那么⊙A与x 轴的位置关系是
12.如图,在△ABC中,D是边BC 上的一点,以AD 为直径的⊙O交AC 于点E,连结DE.若⊙O与BC相切,∠ADE=55°,则∠C的度数为 .
13. 如图,∠ACB=60°,半径为1cm的⊙O切BC 于点C,若将⊙O在CB 上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是 cm.
14. 如图,PA,PB是⊙O的切线,A,B为切点,点 C,D在⊙O上.若∠P=102°,则∠A+∠C= .
15. 如图,AB为半圆O的直径,C为半圆弧的三等分点,过B,C两点的半圆O 的切线交于点P,若AB的长是2a,则 PA的长是 .
16. 如图,在矩形 ABCD中,AB=4,AD=3,以点C为圆心作⊙C 与直线BD 相切,点P 是⊙C 上一个动点,连结AP交BD 于点T,则 的最大值是 .
三、解答题(本大题有8小题,共66分)
17.(6分)已知:如图,在△OAB中,OA=OB,⊙O与AB 相切于点C.求证:AC=BC.小明同学的证明过程如下框:
证明:连结OC,
∵OA=OB,
∴∠A=∠B,
又∵OC=OC,
∴△OAC≌△OBC,
∴AC=BC.
小明的证法是否正确 若正确,请在框内打“ ”;若错误,请写出你的证明过程.
18. (6分)如图,已知⊙O的直径 弦AC=8,D是 的中点,过点D作 交AC的延长线于点E.
(1)求证:DE 是⊙O的切线;
(2)求AE的长.
19.(6分)如图所示,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心 P在AC边上,且与AB,BC 两边都相切(保留作图痕迹,不写作法和证明);
(2)若 求⊙P的面积.
20.(8分)如图①,A 是⊙O直径上一点,OB是和这条直径垂直的半径,BA的延长线和⊙O相交于另一点C,过C点的切线和OA 的延长线相交于点 D.
(1) 求证:
(2)将直线 DA 向上平移,如图②,使AD 和OB 垂直的关系不变,CD 仍是⊙O的切线,那么 DA 与DC 存在什么关系 请根据图②写出你的猜想,并证明你的猜想.
21.(8分)如图,在 中, 以AB为直径作⊙O,点D为⊙O上一点,且( ,连结DO并延长交CB的延长线于点E,连结AC.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若 求圆的半径及AC的长.
22.(10分)如图,AD是⊙O的直径,AB为⊙O的弦, ,OP 与AB 的延长线交于点 P,过B点的⊙O的切线交OP 于点C,连结BD.
(1)求证:
(2)若 求线段 BP 的长.
23.(10分)如图,点 A,B,C在半径为8的⊙O上,过点 B 作. ,交OA 延长线于点 D.连结 BC,且
(1)求证:BD是⊙O的切线;
(2)求图中阴影部分的面积.
24.(12分)如图,AB是⊙O的直径,点 D在AB 的延长线上,C,E是⊙O上的两点, 延长AE交BC的延长线于点 F.
(1)求证:CD是⊙O的切线;
(2)求证:
(3)若 求弦 AC的长.
第2章 直线与圆的位置关系
1. B 2. C 3. B 4. D 5. D 6. A7.C 8. C 9. C
10. D 解析:如图,设直线 与x轴交于点C,与y轴交于点D,作OH⊥CD于点H,当x=0时, 则 当y=0时 解得x=-2,则 C(-2,0),∴ 连 结 OP,OA,如图,∵PA为⊙O 的切线,∴ OA ⊥ PA, ∴ PA = 当OP 的值最小时,PA 的值最小,而OP 的最小值为OH 的长,∴PA的最小值为
11. 相切12. 55° 13. 14. 219
15. 16. 3
17. 解:证法错误.证明:连结OC,∵⊙O与AB 相切于点C,∴OC⊥AB,又∵OA=OB,∴AC=BC.
18. (1)证明:如图,连结OD,∵D是 的中点, =DC,∴∠BOD=∠BAE,∴OD∥AE,∵DE⊥AC,∴∠AED=90°,∴∠ODE=90°.∴OD⊥DE,∴DE是⊙O的切线C
(2)解:如图,过点 O作OF⊥AC 于点 F, 四边形OFED 是矩形, =10,∴FE=5,∴AE=AF+FE=5+4=9.
19. 解:(1)如图所示,则⊙P 即为所求作的圆.
(2)∵∠ABC=60°,BP 平分∠ABC,∴∠ABP= ∴S⊙P=3π.
20. (1)证明:连结OC,∵CD是切线,∴∠OCD=90°,∴∠DCA+∠OCB=90°.∵OB⊥OA,
∴∠OAB+∠B=90°,∵∠B=∠OCB,∴∠OAB=∠DCA.∵∠OAB=∠DAC,∴∠DAC=∠DCA,∴DA=DC.
(2)解:DC=DA.证明同上.
21. 解:(1)CD 与⊙O 相切.理由:连结OC.∵CB=CD,CO= CO,OB = OD,∴△OCB≌△OCD(SSS),∴∠ODC=∠OBC=90°,∴OD⊥DC,∴DC是⊙O的切线. (2)设⊙O的半径为r.在 Rt△OBE中, CD=BC=3,在 Rt△ABC中, 圆的半径为 1.5,AC 的长为
22. (1)证明:连结OB,如图,∵AD是⊙O的直径,∴∠ABD=90°,∴∠A+∠ADB=90°,∵BC 为切线,∴OB⊥BC,∴∠OBC= 而OA = OB, ∴∠A = ∠OBA,∴∠CBP=∠ADB. (2)解:∵ 即
23. (1)证明:连结OB,交 CA于点E,∵∠C=30°,∠C 即OB⊥AC,∵BD∥ AC, ∴∠DBE =∠AEO= 90°,∴BD 是⊙O的切线. (2)解: ∴∠D=∠OAC=30°,∵∠OBD=90°,OB=8,∴
24. (1)证明:如图,连结OC,∵AB是⊙O 的直径,∴∠ACB=90°,∴∠CAD+∠ABC=90°, ∠CAE=∠CAB,∵∠BCD=∠CAE,∴∠CAB=∠BCD,∵OB = OC, ∴∠OBC = ∠OCB, ∴∠OCB +∠BCD=90°,∴∠OCD=90°,∴CD是⊙O的切线.
(2)证明:∵∠BAC =∠CAE,∠ACB =∠ACF = 90°, AC = AC, ∴△ABC≌△AFC(ASA),∴CB=CF,又∵CB=CE,∴CE=CF.
(3)解:∵∠BCD=∠CAD,∠ADC=∠CDB,∴ 2,∴AB=AD-BD=2-1=1,设BC=a,AC a由勾股定理可得: 解得:
