浙教版数学九年级下册 第3章 三视图与表面展开图(含答案)
文档属性
| 名称 | 浙教版数学九年级下册 第3章 三视图与表面展开图(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-16 07:12:09 | ||
图片预览

文档简介
第3 章 三视图与表面展开图
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
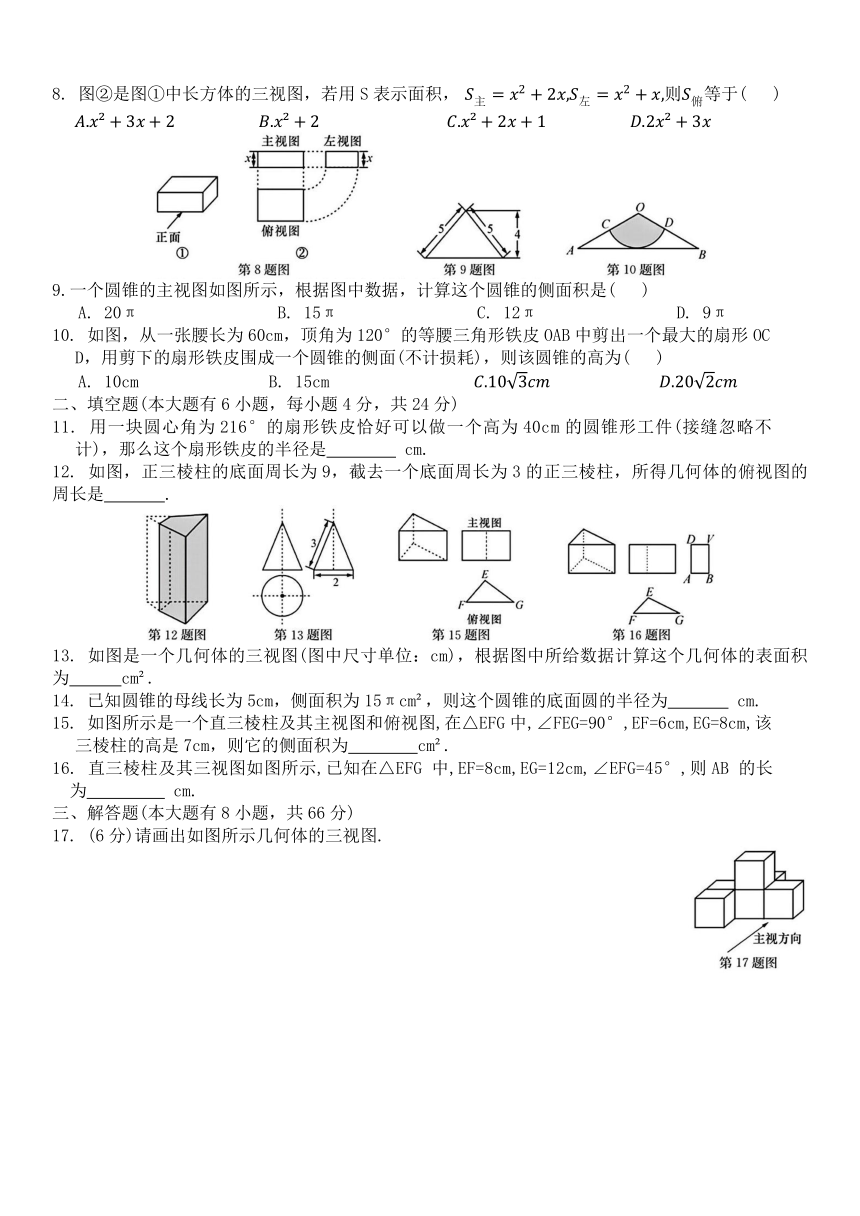
1.下列几何体中,俯视图是圆的几何体是( )
2.如下摆放的几何体中,主视图与左视图有可能不同的是( )
3.如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是( )
A. 15π
B. 30π
C. 45π
D. 60π
4.下列关于图中物体的主视图画法正确的是( )
5. 已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是 ( )
A. 4π B. 8π C. 12π D. 16π
6. 如图,空心卷筒纸的高度为12cm,外径(直径)为10cm,内径为4cm,在比例尺为1:4 的三视图中,其主视图的面积是( )
C. 30cm
7. 如图是由7个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的左视图是( )
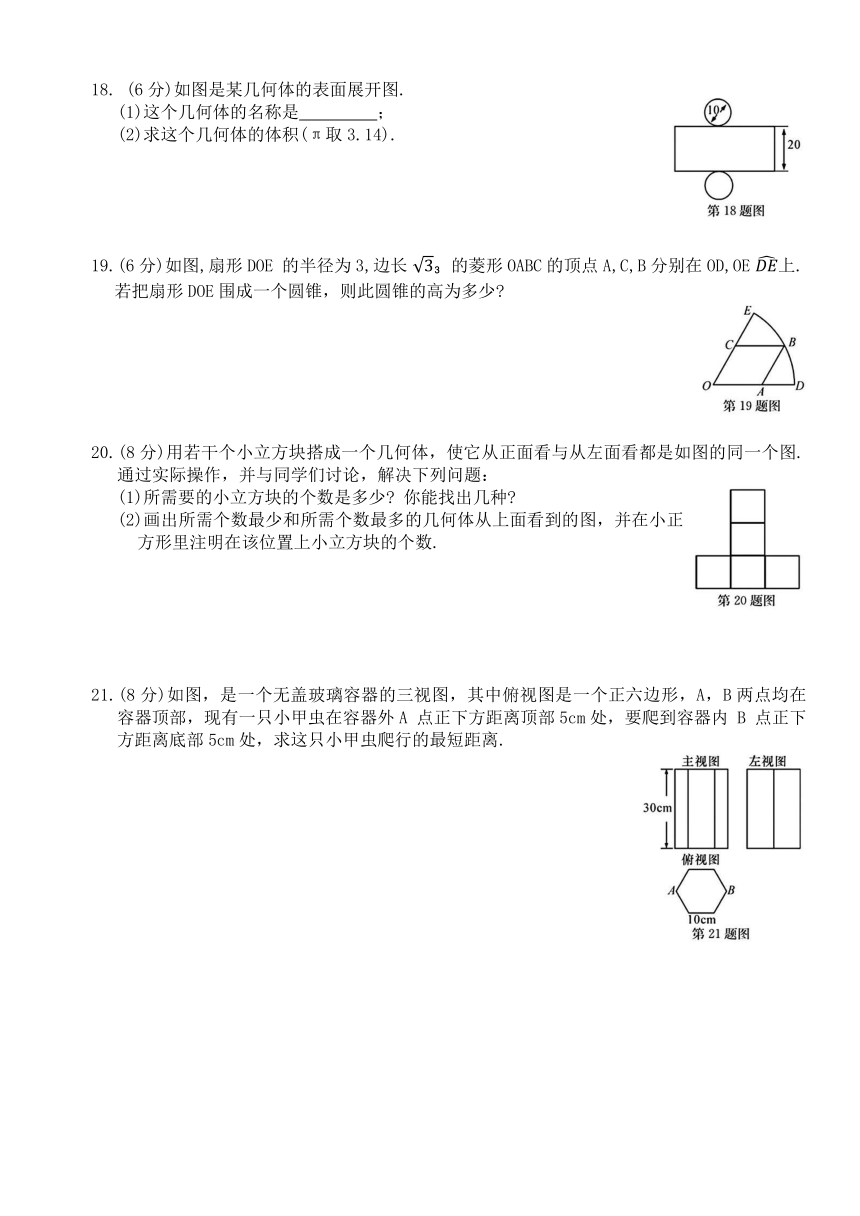
8. 图②是图①中长方体的三视图,若用S表示面积, 则等于( )
9.一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是( )
A. 20π B. 15π C. 12π D. 9π
10. 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
A. 10cm B. 15cm
二、填空题(本大题有6小题,每小题4分,共24分)
11. 用一块圆心角为216°的扇形铁皮恰好可以做一个高为40cm的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是 cm.
12. 如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .
13. 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所给数据计算这个几何体的表面积为 cm .
14. 已知圆锥的母线长为5cm,侧面积为15πcm ,则这个圆锥的底面圆的半径为 cm.
15. 如图所示是一个直三棱柱及其主视图和俯视图,在△EFG中,∠FEG=90°,EF=6cm,EG=8cm,该三棱柱的高是7cm,则它的侧面积为 cm .
16. 直三棱柱及其三视图如图所示,已知在△EFG 中,EF=8cm,EG=12cm,∠EFG=45°,则AB 的长为 cm.
三、解答题(本大题有8小题,共66分)
17. (6分)请画出如图所示几何体的三视图.
18. (6分)如图是某几何体的表面展开图.
(1)这个几何体的名称是 ;
(2)求这个几何体的体积(π取3.14).
19.(6分)如图,扇形DOE 的半径为3,边长 的菱形OABC的顶点A,C,B分别在OD,OE 上.若把扇形DOE围成一个圆锥,则此圆锥的高为多少
20.(8分)用若干个小立方块搭成一个几何体,使它从正面看与从左面看都是如图的同一个图.通过实际操作,并与同学们讨论,解决下列问题:
(1)所需要的小立方块的个数是多少 你能找出几种
(2)画出所需个数最少和所需个数最多的几何体从上面看到的图,并在小正方形里注明在该位置上小立方块的个数.
21.(8分)如图,是一个无盖玻璃容器的三视图,其中俯视图是一个正六边形,A,B两点均在容器顶部,现有一只小甲虫在容器外A 点正下方距离顶部5cm处,要爬到容器内 B 点正下方距离底部5cm处,求这只小甲虫爬行的最短距离.
22.(10分)如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长. ,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
23.(10分)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所给数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
24.(12分)如图①为一上面无盖的正方体纸盒,现将其剪开展开成平面图,如图②所示.已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出的最长线段的长度,这样的线段可画几条
(2)试比较立体图中 与平面展开图中∠B'A'C'的大小关系.
第3章 三视图与表面展开图
1. A 2. D 3. D 4. C 5. C 6. D 7. C8. A 9. B 10. D 11. 50 12. 8 13. 4π14. 3 15. 168 16. 17 略
18. 解:(1)圆柱 (2)体积为:3
19. 解:连结OB,AC交于点 F.∵四边形OABC 是形,∴AC⊥BO,CF=AF,FO=BF,∠COB=∠BOA.又∵扇形DOE 的半径为3,∴FO= Br= ∴∠FOC=30°,∴∠EOD=2×30°=60°.设圆锥底面半径为r,则由圆锥侧面展开图扇形的圆心角公式得 解得 又∵圆锥的母线长为3,∴此圆锥的高为
20. 解:(1)3+2=5(个),9+2=11(个),故所需要的小立方块的个数是5~11个,能找出7种.
(2)
21. 解:如图所示:A'B的长即为最短路径长,在 中,BC 答:这只小甲虫爬行的最短距离是
22. 解:由题意可知: 设∠AOB=n,AO=R,则CO=R-9,由弧长公式得 则∴ 解得 n=40,R=27,故扇形OAB的圆心角是 40度.∵R=27,R-9=18, .纸杯侧面积: 纸杯底面积=π· 纸杯表面积
23. 解:(1)圆锥
(2)表面积 (3)如图,将圆锥侧面展开,连结BB',交 AC 于点 D',由条件得, C 为弧. 的中点,所以 的位置即为 D 的位置,∴线段 BD的长为所求的最短路程,
24. 解:(1)在平面展开图中可画出的最长线段的长度为 如图①中的. 在 中, 由 勾 股 定 理得, 这样的线段可画4条(另三条用虚线标出).
(2)∵立体图中. 为等腰直角三角形的一个锐角, 在平面展开图中,连结线段B'C',如图②.由勾股定理可得: 由勾股定理的逆定理可得△A'B'C'为直角三角形.又 △A'B'C'为等腰直角三角形,. ∠BAC 与∠BA'C'相等.
班级 学号 得分 姓名
一、选择题(本大题有10小题,每小题3分,共30分)
1.下列几何体中,俯视图是圆的几何体是( )
2.如下摆放的几何体中,主视图与左视图有可能不同的是( )
3.如图,圆锥的底面半径r=6,高h=8,则圆锥的侧面积是( )
A. 15π
B. 30π
C. 45π
D. 60π
4.下列关于图中物体的主视图画法正确的是( )
5. 已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是 ( )
A. 4π B. 8π C. 12π D. 16π
6. 如图,空心卷筒纸的高度为12cm,外径(直径)为10cm,内径为4cm,在比例尺为1:4 的三视图中,其主视图的面积是( )
C. 30cm
7. 如图是由7个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,这个几何体的左视图是( )
8. 图②是图①中长方体的三视图,若用S表示面积, 则等于( )
9.一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是( )
A. 20π B. 15π C. 12π D. 9π
10. 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
A. 10cm B. 15cm
二、填空题(本大题有6小题,每小题4分,共24分)
11. 用一块圆心角为216°的扇形铁皮恰好可以做一个高为40cm的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是 cm.
12. 如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .
13. 如图是一个几何体的三视图(图中尺寸单位:cm),根据图中所给数据计算这个几何体的表面积为 cm .
14. 已知圆锥的母线长为5cm,侧面积为15πcm ,则这个圆锥的底面圆的半径为 cm.
15. 如图所示是一个直三棱柱及其主视图和俯视图,在△EFG中,∠FEG=90°,EF=6cm,EG=8cm,该三棱柱的高是7cm,则它的侧面积为 cm .
16. 直三棱柱及其三视图如图所示,已知在△EFG 中,EF=8cm,EG=12cm,∠EFG=45°,则AB 的长为 cm.
三、解答题(本大题有8小题,共66分)
17. (6分)请画出如图所示几何体的三视图.
18. (6分)如图是某几何体的表面展开图.
(1)这个几何体的名称是 ;
(2)求这个几何体的体积(π取3.14).
19.(6分)如图,扇形DOE 的半径为3,边长 的菱形OABC的顶点A,C,B分别在OD,OE 上.若把扇形DOE围成一个圆锥,则此圆锥的高为多少
20.(8分)用若干个小立方块搭成一个几何体,使它从正面看与从左面看都是如图的同一个图.通过实际操作,并与同学们讨论,解决下列问题:
(1)所需要的小立方块的个数是多少 你能找出几种
(2)画出所需个数最少和所需个数最多的几何体从上面看到的图,并在小正方形里注明在该位置上小立方块的个数.
21.(8分)如图,是一个无盖玻璃容器的三视图,其中俯视图是一个正六边形,A,B两点均在容器顶部,现有一只小甲虫在容器外A 点正下方距离顶部5cm处,要爬到容器内 B 点正下方距离底部5cm处,求这只小甲虫爬行的最短距离.
22.(10分)如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长. ,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
23.(10分)如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所给数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
24.(12分)如图①为一上面无盖的正方体纸盒,现将其剪开展开成平面图,如图②所示.已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出的最长线段的长度,这样的线段可画几条
(2)试比较立体图中 与平面展开图中∠B'A'C'的大小关系.
第3章 三视图与表面展开图
1. A 2. D 3. D 4. C 5. C 6. D 7. C8. A 9. B 10. D 11. 50 12. 8 13. 4π14. 3 15. 168 16. 17 略
18. 解:(1)圆柱 (2)体积为:3
19. 解:连结OB,AC交于点 F.∵四边形OABC 是形,∴AC⊥BO,CF=AF,FO=BF,∠COB=∠BOA.又∵扇形DOE 的半径为3,∴FO= Br= ∴∠FOC=30°,∴∠EOD=2×30°=60°.设圆锥底面半径为r,则由圆锥侧面展开图扇形的圆心角公式得 解得 又∵圆锥的母线长为3,∴此圆锥的高为
20. 解:(1)3+2=5(个),9+2=11(个),故所需要的小立方块的个数是5~11个,能找出7种.
(2)
21. 解:如图所示:A'B的长即为最短路径长,在 中,BC 答:这只小甲虫爬行的最短距离是
22. 解:由题意可知: 设∠AOB=n,AO=R,则CO=R-9,由弧长公式得 则∴ 解得 n=40,R=27,故扇形OAB的圆心角是 40度.∵R=27,R-9=18, .纸杯侧面积: 纸杯底面积=π· 纸杯表面积
23. 解:(1)圆锥
(2)表面积 (3)如图,将圆锥侧面展开,连结BB',交 AC 于点 D',由条件得, C 为弧. 的中点,所以 的位置即为 D 的位置,∴线段 BD的长为所求的最短路程,
24. 解:(1)在平面展开图中可画出的最长线段的长度为 如图①中的. 在 中, 由 勾 股 定 理得, 这样的线段可画4条(另三条用虚线标出).
(2)∵立体图中. 为等腰直角三角形的一个锐角, 在平面展开图中,连结线段B'C',如图②.由勾股定理可得: 由勾股定理的逆定理可得△A'B'C'为直角三角形.又 △A'B'C'为等腰直角三角形,. ∠BAC 与∠BA'C'相等.
