浙教版数学九年级上册 4.5相似三角形的应用 讲义(无答案)
文档属性
| 名称 | 浙教版数学九年级上册 4.5相似三角形的应用 讲义(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 739.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-16 00:00:00 | ||
图片预览


文档简介
相似三角形的应用
班级 姓名 学号
精讲精练
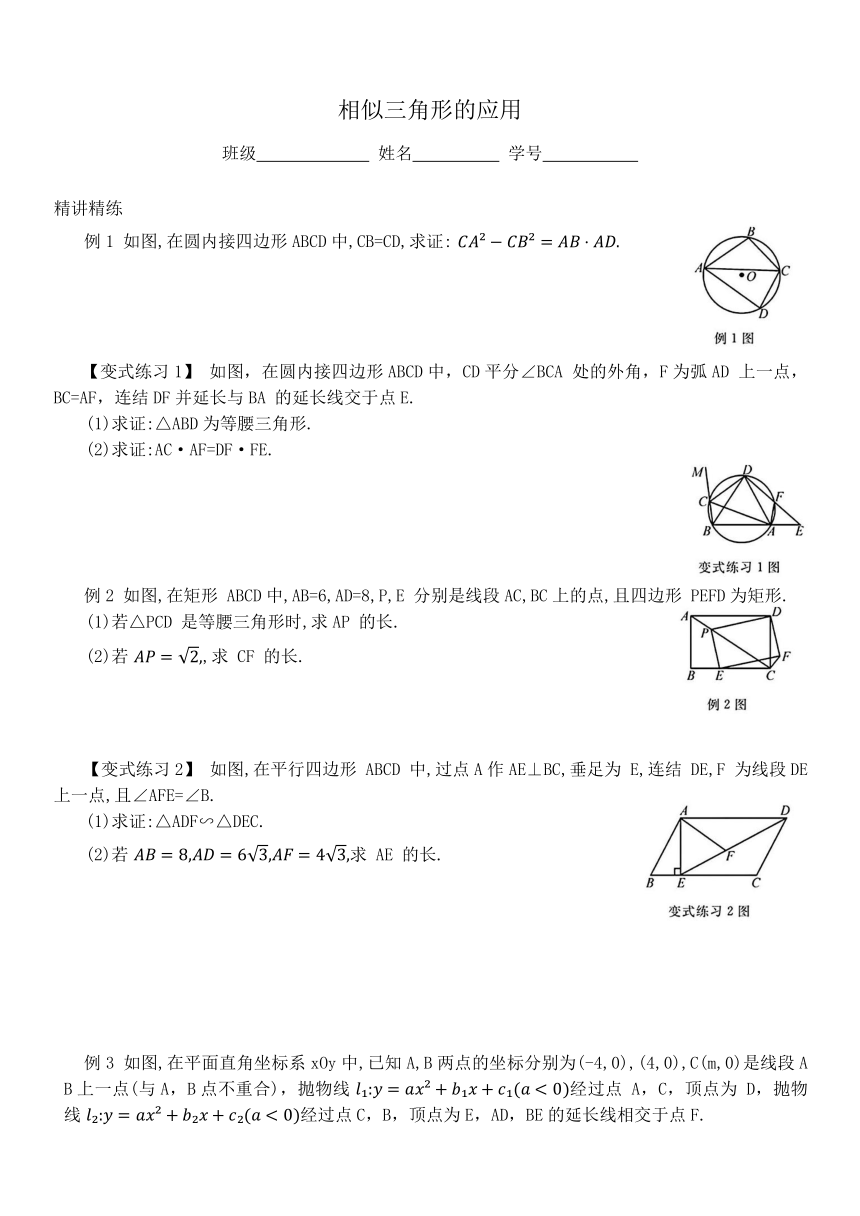
例1 如图,在圆内接四边形ABCD中,CB=CD,求证:
【变式练习1】 如图,在圆内接四边形ABCD中,CD平分∠BCA 处的外角,F为弧AD 上一点,BC=AF,连结DF并延长与BA 的延长线交于点E.
(1)求证:△ABD为等腰三角形.
(2)求证:AC·AF=DF·FE.
例2 如图,在矩形 ABCD中,AB=6,AD=8,P,E 分别是线段AC,BC上的点,且四边形 PEFD为矩形.
(1)若△PCD 是等腰三角形时,求AP 的长.
(2)若 ,求 CF 的长.
【变式练习2】 如图,在平行四边形 ABCD 中,过点A作AE⊥BC,垂足为 E,连结 DE,F 为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC.
(2)若 求 AE 的长.
例3 如图,在平面直角坐标系xOy中,已知A,B两点的坐标分别为(-4,0),(4,0),C(m,0)是线段AB上一点(与A,B点不重合),抛物线 经过点 A,C,顶点为 D,抛物线 经过点C,B,顶点为E,AD,BE的延长线相交于点F.
(1)若 求抛物线 的表达式.
(2)若 求 m 的值.
【变式练习3】 如图,二次函数 的图象与x轴交于A(-4,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的表达式.
(2)点M在该抛物线的对称轴上,当 是直角三角形时,求点 M 的坐标.
课后作业
1. 如图,在 中,AD 是中线, ,则线段AC的长为( )
A. 4
C. 6
2. 如图,在 中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
3. 如图,在四边形 ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点 H为垂足.设 AD=y,则y关于x的函数关系用图象大致可以表示为( )
4. 如图, ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB 于点E,交BD于点 F,且∠ABC= 60°,AB=2BC,连结OE.下列结论:①∠ACD=30°;②S ABCD=AC·BC;③OE: AC = :6 成立的个数是( )
A. 1 B. 2 C. 3 D. 4
5. 如图,已知四边形 ABCD,AC与 BD 相交于点 O, 则
6. 如图,在△ABC中,点 D,E 分别是边AB,AC的中点,DF过EC 的中点G 并与BC 的延长线交于点F,BE 与DF 交于点O.若△ADE的面积为 4,则四边形 BOGC的面积= .
7. 如图,正方形OABC的边长为4,点A,C分别在y轴和x 轴的正半轴上,动点 P从点A 出发,以每秒2个单位长度的速度在线段 AB上来回运动,动点 Q从点B 出发,以每秒1个单位长度的速度沿 B→C→O的方向向点O运动,P,Q两点同时出发,当点 Q到达点O时,两点同时停止运动,设运动时间为t(s).
(1)当t=1时,求直线PQ的表达式.
(2)当点 Q在BC 上运动时,若以 P,B,Q为顶点的三角形与 相似,求t 的值.
(3)在P,Q运动过程中,若△OPQ的面积为6,请直接写出满足条件的点 P 的坐标.
8. 如图,抛物线 经过A(0,4),B(4,0),C(-1,0)三点,过点A作垂直于y轴的直线l,在抛物线上有一动点 P,过点 P 作直线PQ∥y轴交直线l 于点 Q,连结 AP.
(1)求抛物线的表达式.
(2)是否存在点 P,使得以 A,P,Q三点构成的三角形与△AOC 相似,若存在,求出点 P 的坐标;若不存在,请说明理由.
(3)当点 P位于抛物线 的对称轴的右侧,若将△APQ沿AP 对折,点Q的对应点为点M,当点M落在坐标轴上时,求直线 AP 的表达式.
走进重高
1. 如图,CB=CA,∠ACB=90°,点 D在边BC 上(与 B,C 不重合),四边形 ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连结FB,交 DE 于点Q,给出以下结论:①AC=FG;②S△FAB :S四边形CBFG=1:2;③∠ABC=∠ABF;④AD =FQ·AC,其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
2.【性质探究】
如图,在矩形ABCD中,对角线 AC,BD 相交于点O,AE平分∠BAC,交 BC于点 E.作 DF⊥AE 于点H,分别交 AB,AC 于点 F,G.
(1)判断△AFG的形状并说明理由.
(2)求证:BF=2OG.
【迁移应用】
(3)记△DGO的面积为S ,△DBF的面积为S ,当 时,求 的值.
班级 姓名 学号
精讲精练
例1 如图,在圆内接四边形ABCD中,CB=CD,求证:
【变式练习1】 如图,在圆内接四边形ABCD中,CD平分∠BCA 处的外角,F为弧AD 上一点,BC=AF,连结DF并延长与BA 的延长线交于点E.
(1)求证:△ABD为等腰三角形.
(2)求证:AC·AF=DF·FE.
例2 如图,在矩形 ABCD中,AB=6,AD=8,P,E 分别是线段AC,BC上的点,且四边形 PEFD为矩形.
(1)若△PCD 是等腰三角形时,求AP 的长.
(2)若 ,求 CF 的长.
【变式练习2】 如图,在平行四边形 ABCD 中,过点A作AE⊥BC,垂足为 E,连结 DE,F 为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC.
(2)若 求 AE 的长.
例3 如图,在平面直角坐标系xOy中,已知A,B两点的坐标分别为(-4,0),(4,0),C(m,0)是线段AB上一点(与A,B点不重合),抛物线 经过点 A,C,顶点为 D,抛物线 经过点C,B,顶点为E,AD,BE的延长线相交于点F.
(1)若 求抛物线 的表达式.
(2)若 求 m 的值.
【变式练习3】 如图,二次函数 的图象与x轴交于A(-4,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的表达式.
(2)点M在该抛物线的对称轴上,当 是直角三角形时,求点 M 的坐标.
课后作业
1. 如图,在 中,AD 是中线, ,则线段AC的长为( )
A. 4
C. 6
2. 如图,在 中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
3. 如图,在四边形 ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点 H为垂足.设 AD=y,则y关于x的函数关系用图象大致可以表示为( )
4. 如图, ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB 于点E,交BD于点 F,且∠ABC= 60°,AB=2BC,连结OE.下列结论:①∠ACD=30°;②S ABCD=AC·BC;③OE: AC = :6 成立的个数是( )
A. 1 B. 2 C. 3 D. 4
5. 如图,已知四边形 ABCD,AC与 BD 相交于点 O, 则
6. 如图,在△ABC中,点 D,E 分别是边AB,AC的中点,DF过EC 的中点G 并与BC 的延长线交于点F,BE 与DF 交于点O.若△ADE的面积为 4,则四边形 BOGC的面积= .
7. 如图,正方形OABC的边长为4,点A,C分别在y轴和x 轴的正半轴上,动点 P从点A 出发,以每秒2个单位长度的速度在线段 AB上来回运动,动点 Q从点B 出发,以每秒1个单位长度的速度沿 B→C→O的方向向点O运动,P,Q两点同时出发,当点 Q到达点O时,两点同时停止运动,设运动时间为t(s).
(1)当t=1时,求直线PQ的表达式.
(2)当点 Q在BC 上运动时,若以 P,B,Q为顶点的三角形与 相似,求t 的值.
(3)在P,Q运动过程中,若△OPQ的面积为6,请直接写出满足条件的点 P 的坐标.
8. 如图,抛物线 经过A(0,4),B(4,0),C(-1,0)三点,过点A作垂直于y轴的直线l,在抛物线上有一动点 P,过点 P 作直线PQ∥y轴交直线l 于点 Q,连结 AP.
(1)求抛物线的表达式.
(2)是否存在点 P,使得以 A,P,Q三点构成的三角形与△AOC 相似,若存在,求出点 P 的坐标;若不存在,请说明理由.
(3)当点 P位于抛物线 的对称轴的右侧,若将△APQ沿AP 对折,点Q的对应点为点M,当点M落在坐标轴上时,求直线 AP 的表达式.
走进重高
1. 如图,CB=CA,∠ACB=90°,点 D在边BC 上(与 B,C 不重合),四边形 ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连结FB,交 DE 于点Q,给出以下结论:①AC=FG;②S△FAB :S四边形CBFG=1:2;③∠ABC=∠ABF;④AD =FQ·AC,其中正确的结论的个数是( )
A. 1 B. 2 C. 3 D. 4
2.【性质探究】
如图,在矩形ABCD中,对角线 AC,BD 相交于点O,AE平分∠BAC,交 BC于点 E.作 DF⊥AE 于点H,分别交 AB,AC 于点 F,G.
(1)判断△AFG的形状并说明理由.
(2)求证:BF=2OG.
【迁移应用】
(3)记△DGO的面积为S ,△DBF的面积为S ,当 时,求 的值.
同课章节目录
