浙教版数学九年级上册第三章圆的基本性质(含答案)
文档属性
| 名称 | 浙教版数学九年级上册第三章圆的基本性质(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 511.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-23 23:41:33 | ||
图片预览


文档简介
浙教版数学九年级上册第三章圆的基本性质
一、选择题
1.下列说法正确的是( )
A.三个点可以确定一个圆
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.长度相等的弧是等弧
2.已知一个扇形的面积是,弧长是,则这个扇形的半径为( )
A.24 B.22 C.12 D.6
3.如图,点在上,,则的度数是( )
A. B. C. D.
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若BE=5,AE=1,则弦CD的长是( )
A.5 B. C. D.6
5.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A.28° B.30° C.36° D.56°
6.如图,AB为⊙O的直径,点C在⊙O上,若,,则的长为( )
A. B. C. D.
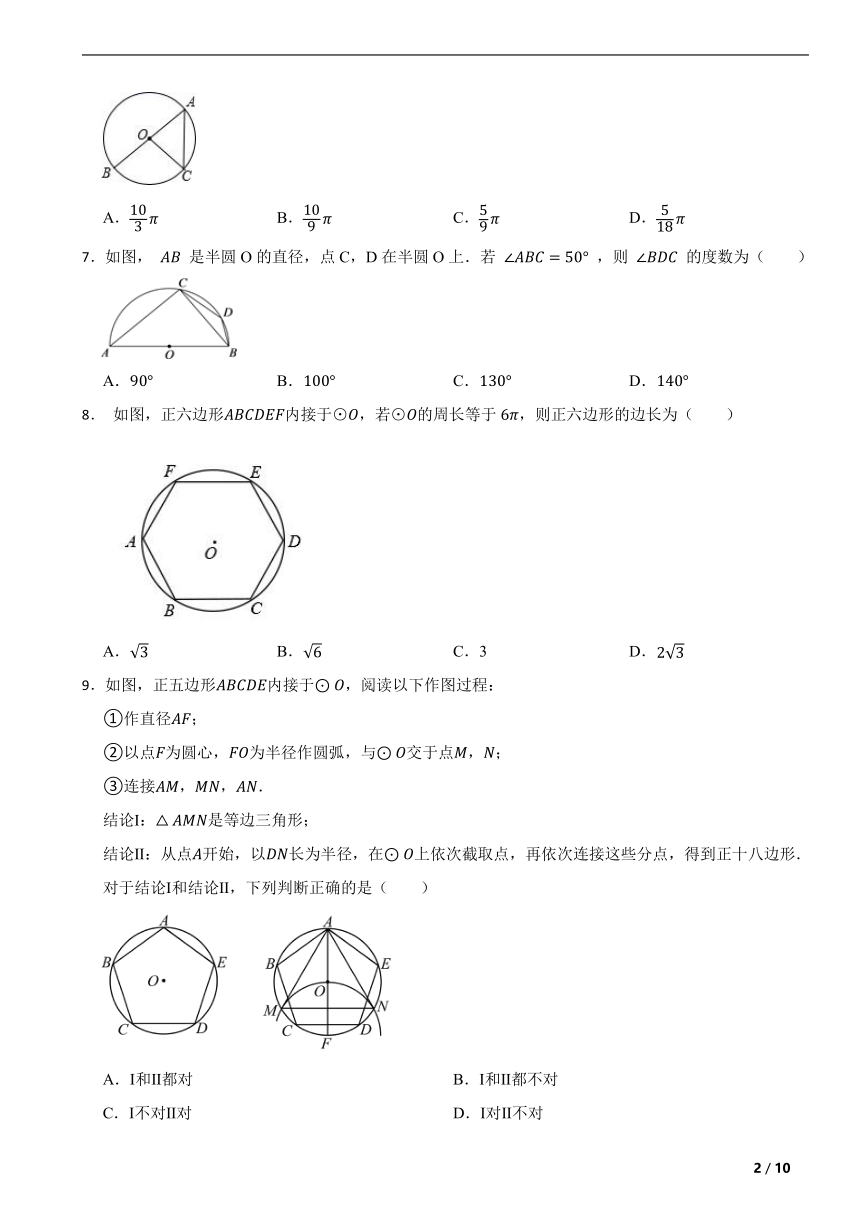
7.如图, 是半圆O的直径,点C,D在半圆O上.若 ,则 的度数为( )
A. B. C. D.
8. 如图,正六边形内接于⊙,若⊙的周长等于,则正六边形的边长为( )
A. B. C.3 D.
9.如图,正五边形内接于,阅读以下作图过程:
①作直径;
②以点为圆心,为半径作圆弧,与交于点,;
③连接,,.
结论Ⅰ:是等边三角形;
结论Ⅱ:从点开始,以长为半径,在上依次截取点,再依次连接这些分点,得到正十八边形.
对于结论Ⅰ和结论Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
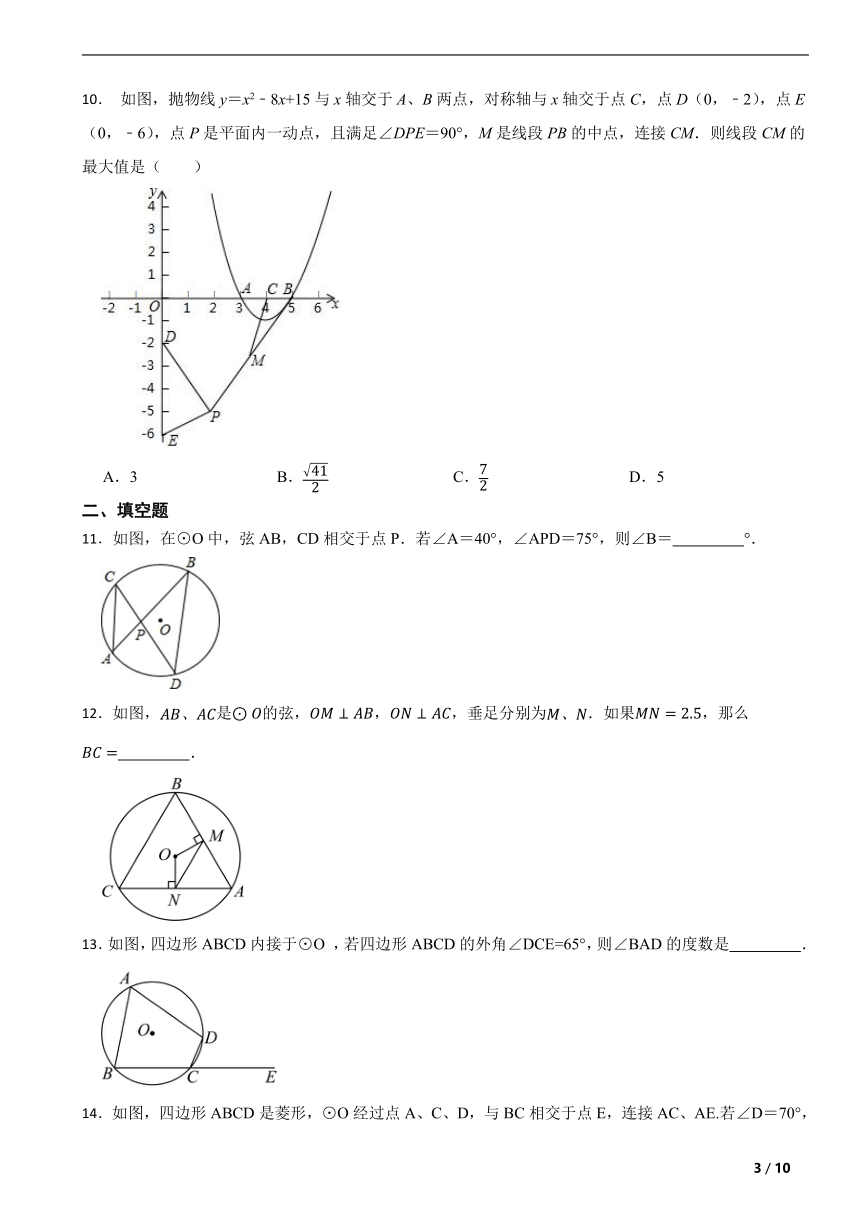
10. 如图,抛物线y=x2﹣8x+15与x轴交于A、B两点,对称轴与x轴交于点C,点D(0,﹣2),点E(0,﹣6),点P是平面内一动点,且满足∠DPE=90°,M是线段PB的中点,连接CM.则线段CM的最大值是( )
A.3 B. C. D.5
二、填空题
11.如图,在⊙O中,弦AB,CD相交于点P.若∠A=40°,∠APD=75°,则∠B= °.
12.如图,是的弦,,,垂足分别为.如果,那么 .
13.如图,四边形ABCD内接于⊙O ,若四边形ABCD的外角∠DCE=65°,则∠BAD的度数是 .
14.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=70°,则∠EAC的度数为 .
15.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为,若用圆内接正十二边形作近似估计,可得的估计值为 .
16.如图,点、,以点为圆心为半径作交轴于两点,点为上一动点,连接,取中点,连接,则的最大值为 .
三、解答题
17.如图,四边形为的内接四边形,是的直径,,.求的度数.
18.如图,OC为⊙O的半径,弦AB⊥OC于点D,OC=10,CD=4,求AB的长.
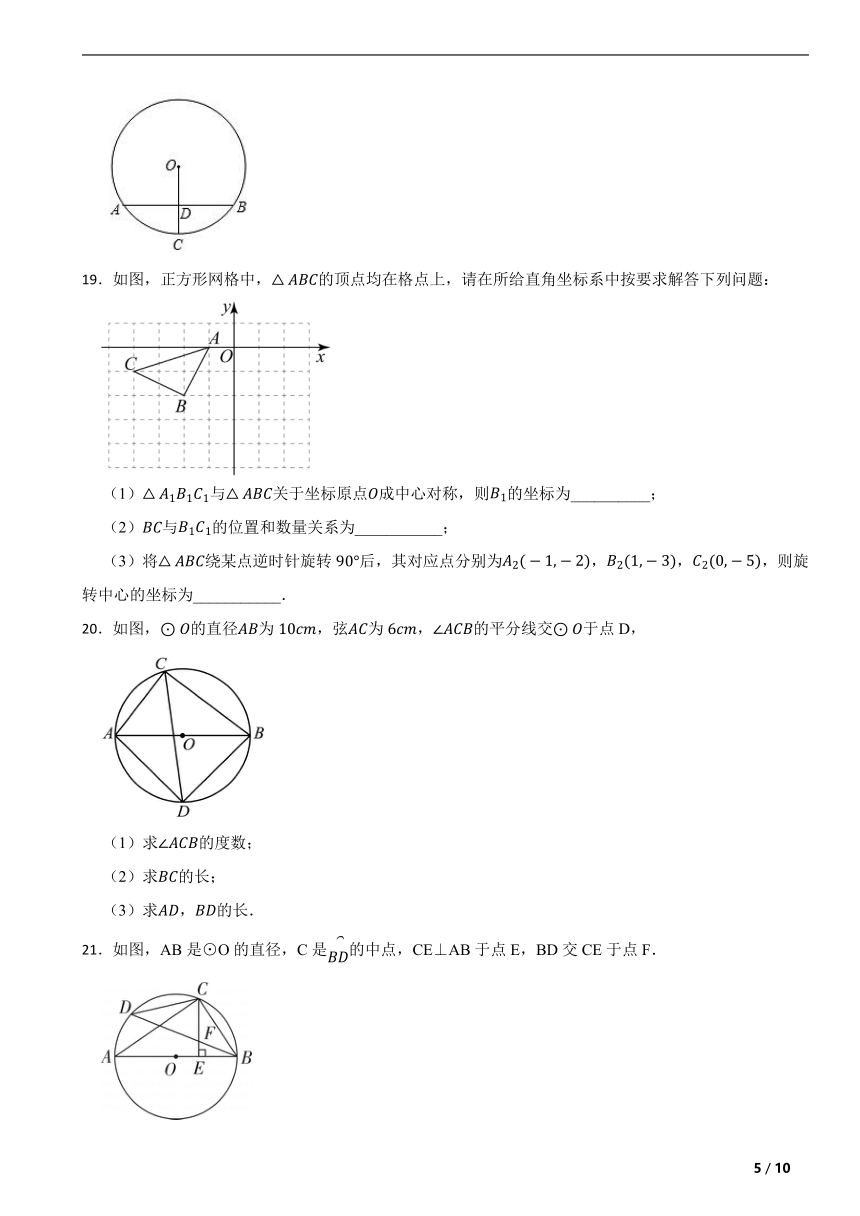
19.如图,正方形网格中,的顶点均在格点上,请在所给直角坐标系中按要求解答下列问题:
(1)与关于坐标原点成中心对称,则的坐标为__________;
(2)与的位置和数量关系为___________;
(3)将绕某点逆时针旋转后,其对应点分别为,,,则旋转中心的坐标为___________.
20.如图,的直径为,弦为,的平分线交于点D,
(1)求的度数;
(2)求的长;
(3)求,的长.
21.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1) 求证:CF=BF.
(2)若CD=6,AC=8,求⊙O的半径及CE的长.
22.如图所示,AB为☉O的直径,AC是☉O的一条弦,D为的中点,作DE⊥AC于点E,交AB的延长线于点F,连接DA.
(1)若AB=90 cm,则圆心O到EF的距离是多少 说明你的理由.
(2)若DA=DF=6,求阴影部分的面积(结果保留π).
23.如图,是的直径,弦与点,已知,点为上任意一点,(点不与重合),连结并延长与交于点,连.
(1)求的长.
(2)若,直接写出的长.
(3)①若点在之间(点不与点重合),求证:.
②若点在之间(点不与点重合),求与满足的关系.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】D
8.【答案】C
9.【答案】D
10.【答案】C
11.【答案】35
12.【答案】
13.【答案】65°
14.【答案】15°
15.【答案】3
16.【答案】
17.【答案】
18.【答案】16
19.【答案】(1);
(2)平行且相等;
(3).
20.【答案】(1)
(2)
(3)
21.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=90°-∠ABC.
∵CE⊥AB,
∴∠ECB=90°-∠ABC,
∴∠ECB=∠A.
又∵C是的中点,
∴,
∴∠DBC=∠A,
∴∠ECB=∠DBC,
∴CF= BF;
(2)解:∵,
∴BC=CD=6.
在Rt△ABC中,AB= =10,
∴⊙O的半径为5;
∵S△ABC= AB×CE= BC×AC,
∴CE= .
22.【答案】(1)解:如图所示,连接OD,
∵D为的中点,
∴∠CAD=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO.
∴∠CAD=∠ADO.∴OD∥AE.
∵DE⊥AC,∴OD⊥EF.
∴OD的长是圆心O到EF的距离.
∵AB=90 cm,∴OD=AB=45 cm.
(2)解:如图所示,过点O作OG⊥AD交AD于点G.
∵DA=DF,∴∠F=∠BAD.
由(1),得∠CAD=∠BAD,
∴∠F=∠CAD.
∵∠F+∠BAD+∠CAD=90°,
∴∠F=∠BAD=∠CAD=30°.
∴∠BOD=2∠BAD=60°,OF=2OD.
∵在Rt△ODF中,OF2-OD2=DF2,
∴(2OD)2-OD2=(6)2,解得OD=6.
在Rt△OAG中,OA=OD=6,∠OAG=30°,AG==3,AD=2,
S△AOD=×6×3=9.
∴S阴影=S扇形OBD+S△AOD=+9=6π+9.
23.【答案】(1)解:连接OD,
∵直径AB=10,AE=8,∴BE=2.∴OE=5-2=3.
又∵AB⊥CD,在Rt△PED中,
∴ED=
∴CD=2ED=8
(2)解:若CP=PQ,则点P与点O重合,或点P与点E重合.
所以AP=5或8
(3)解:①连接AC,由图可知∠ACQ=∠ADQ,
因为AB是⊙O的直径,AB⊥CD,
所以CE=DE,即AB是CD的垂直平分线,
所以AC=AD,PC=PD,
因为AP=AP,
所以△ACP≌△ADP(SSS),
所以∠ACP=∠ADP,
所以∠ADP=∠ADQ.
②∠ADP+∠ADQ=180°.
理由如下:
连接AC,
因为AB是直径,AB⊥CD,
所以AC=AD,CE=DE,
所以△ACP≌△ADP(SSS),
所以∠ACP=∠ADP,
因为∠ACP=,∠ADQ=,
所以∠ACP+∠ADQ=(+)=180°.
1 / 1
一、选择题
1.下列说法正确的是( )
A.三个点可以确定一个圆
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.长度相等的弧是等弧
2.已知一个扇形的面积是,弧长是,则这个扇形的半径为( )
A.24 B.22 C.12 D.6
3.如图,点在上,,则的度数是( )
A. B. C. D.
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若BE=5,AE=1,则弦CD的长是( )
A.5 B. C. D.6
5.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A.28° B.30° C.36° D.56°
6.如图,AB为⊙O的直径,点C在⊙O上,若,,则的长为( )
A. B. C. D.
7.如图, 是半圆O的直径,点C,D在半圆O上.若 ,则 的度数为( )
A. B. C. D.
8. 如图,正六边形内接于⊙,若⊙的周长等于,则正六边形的边长为( )
A. B. C.3 D.
9.如图,正五边形内接于,阅读以下作图过程:
①作直径;
②以点为圆心,为半径作圆弧,与交于点,;
③连接,,.
结论Ⅰ:是等边三角形;
结论Ⅱ:从点开始,以长为半径,在上依次截取点,再依次连接这些分点,得到正十八边形.
对于结论Ⅰ和结论Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对
C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
10. 如图,抛物线y=x2﹣8x+15与x轴交于A、B两点,对称轴与x轴交于点C,点D(0,﹣2),点E(0,﹣6),点P是平面内一动点,且满足∠DPE=90°,M是线段PB的中点,连接CM.则线段CM的最大值是( )
A.3 B. C. D.5
二、填空题
11.如图,在⊙O中,弦AB,CD相交于点P.若∠A=40°,∠APD=75°,则∠B= °.
12.如图,是的弦,,,垂足分别为.如果,那么 .
13.如图,四边形ABCD内接于⊙O ,若四边形ABCD的外角∠DCE=65°,则∠BAD的度数是 .
14.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=70°,则∠EAC的度数为 .
15.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为,若用圆内接正十二边形作近似估计,可得的估计值为 .
16.如图,点、,以点为圆心为半径作交轴于两点,点为上一动点,连接,取中点,连接,则的最大值为 .
三、解答题
17.如图,四边形为的内接四边形,是的直径,,.求的度数.
18.如图,OC为⊙O的半径,弦AB⊥OC于点D,OC=10,CD=4,求AB的长.
19.如图,正方形网格中,的顶点均在格点上,请在所给直角坐标系中按要求解答下列问题:
(1)与关于坐标原点成中心对称,则的坐标为__________;
(2)与的位置和数量关系为___________;
(3)将绕某点逆时针旋转后,其对应点分别为,,,则旋转中心的坐标为___________.
20.如图,的直径为,弦为,的平分线交于点D,
(1)求的度数;
(2)求的长;
(3)求,的长.
21.如图,AB是⊙O的直径,C是的中点,CE⊥AB于点E,BD交CE于点F.
(1) 求证:CF=BF.
(2)若CD=6,AC=8,求⊙O的半径及CE的长.
22.如图所示,AB为☉O的直径,AC是☉O的一条弦,D为的中点,作DE⊥AC于点E,交AB的延长线于点F,连接DA.
(1)若AB=90 cm,则圆心O到EF的距离是多少 说明你的理由.
(2)若DA=DF=6,求阴影部分的面积(结果保留π).
23.如图,是的直径,弦与点,已知,点为上任意一点,(点不与重合),连结并延长与交于点,连.
(1)求的长.
(2)若,直接写出的长.
(3)①若点在之间(点不与点重合),求证:.
②若点在之间(点不与点重合),求与满足的关系.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】D
8.【答案】C
9.【答案】D
10.【答案】C
11.【答案】35
12.【答案】
13.【答案】65°
14.【答案】15°
15.【答案】3
16.【答案】
17.【答案】
18.【答案】16
19.【答案】(1);
(2)平行且相等;
(3).
20.【答案】(1)
(2)
(3)
21.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A=90°-∠ABC.
∵CE⊥AB,
∴∠ECB=90°-∠ABC,
∴∠ECB=∠A.
又∵C是的中点,
∴,
∴∠DBC=∠A,
∴∠ECB=∠DBC,
∴CF= BF;
(2)解:∵,
∴BC=CD=6.
在Rt△ABC中,AB= =10,
∴⊙O的半径为5;
∵S△ABC= AB×CE= BC×AC,
∴CE= .
22.【答案】(1)解:如图所示,连接OD,
∵D为的中点,
∴∠CAD=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO.
∴∠CAD=∠ADO.∴OD∥AE.
∵DE⊥AC,∴OD⊥EF.
∴OD的长是圆心O到EF的距离.
∵AB=90 cm,∴OD=AB=45 cm.
(2)解:如图所示,过点O作OG⊥AD交AD于点G.
∵DA=DF,∴∠F=∠BAD.
由(1),得∠CAD=∠BAD,
∴∠F=∠CAD.
∵∠F+∠BAD+∠CAD=90°,
∴∠F=∠BAD=∠CAD=30°.
∴∠BOD=2∠BAD=60°,OF=2OD.
∵在Rt△ODF中,OF2-OD2=DF2,
∴(2OD)2-OD2=(6)2,解得OD=6.
在Rt△OAG中,OA=OD=6,∠OAG=30°,AG==3,AD=2,
S△AOD=×6×3=9.
∴S阴影=S扇形OBD+S△AOD=+9=6π+9.
23.【答案】(1)解:连接OD,
∵直径AB=10,AE=8,∴BE=2.∴OE=5-2=3.
又∵AB⊥CD,在Rt△PED中,
∴ED=
∴CD=2ED=8
(2)解:若CP=PQ,则点P与点O重合,或点P与点E重合.
所以AP=5或8
(3)解:①连接AC,由图可知∠ACQ=∠ADQ,
因为AB是⊙O的直径,AB⊥CD,
所以CE=DE,即AB是CD的垂直平分线,
所以AC=AD,PC=PD,
因为AP=AP,
所以△ACP≌△ADP(SSS),
所以∠ACP=∠ADP,
所以∠ADP=∠ADQ.
②∠ADP+∠ADQ=180°.
理由如下:
连接AC,
因为AB是直径,AB⊥CD,
所以AC=AD,CE=DE,
所以△ACP≌△ADP(SSS),
所以∠ACP=∠ADP,
因为∠ACP=,∠ADQ=,
所以∠ACP+∠ADQ=(+)=180°.
1 / 1
同课章节目录
