浙教版数学七上第二章 有理数的运算--第三章 实数 综合复习试卷(含答案)
文档属性
| 名称 | 浙教版数学七上第二章 有理数的运算--第三章 实数 综合复习试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 332.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-24 15:46:49 | ||
图片预览


文档简介
浙教版数学七上第二章-第三章
一、选择题
1. 2023年9月23日晚,杭州亚运会开幕式现场,超过1.05亿名线上火炬手汇聚而成的“数字火炬手”与现场真实的火炬手一起,共同点燃亚运之火,创造了新的吉尼斯世界纪录.其中数据1.05亿用科学记数法可表示为( )
A. B. C. D.
2.是2023的( )
A.倒数 B.绝对值 C.相反数 D.平方根
3.已知算式的值为0,则“”内应填入的运算符号为( )
A. B. C. D.
4.如表所示的是琳琳作业中的一道题目,“”处都是0但发生破损,琳琳查阅后发现本题答案为1,则破损处“0”的个数为( )
已知:60,求的值
A.4 B.5 C.6 D.7
5.池塘里的睡莲的面积每天长大一倍,若经过13天就可以长满整个池塘,则这些睡莲长满半个池塘需要( )
A.6 B.7 C.10 D.12
6.如图,数轴上的四个点、、、位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,ABA. B. C. D.
7.的个位数字为( )
A.1 B.3 C.7 D.9
8.我们把不超过有理数的最大整数称为的整数部分,记作,又把称为的小数部分,记作,则有.如:,,.下列说法中正确的有( )个
①;
②;
③若,且,则或;
④方程的解为或.
A.1 B.2 C.3 D.4
9.法国的“小九九”从“一 一得一”到“五五二十五”和我国的“小九九”是一样的,后面的就改用手势了.下面两个图框是用法国“小九九”计算和的两个示例,且左手伸出的手指数不大于右手伸出的手指数.若用法国的“小九九”计算,左、右手依次伸出手指的个数是( )
?
因为两手伸出的手指数的和为,未伸出的手指数的积为,所以 ?
因为两手伸出的手指数的和为,未伸出的手指数的积为,所以
A., B., C., D.,
10.“幻方”在中国古代称为“河图”、“洛书”,又叫“纵横图”.其主要性质是在一个由若干个排列整齐的数组成的正方形中,图中任意一横行,一纵行及对角线的几个数之和都相等.图(l)所示是一个幻方.有人建议向火星发射如图(2)所示的幻方图案,如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).图(3)是一个未完成的幻方,请你类比图(l)推算图(3)中处所对应的数字是( )
A.1 B.2 C.3 D.4
二、填空题
11.用四舍五入把3.1426精确到百分位,所得到的近似数是 .
12.计算: .
13.数的位置如图,化简 .
14.规定三数a,b,c之间的一种运算:如果,那么.例如:因为,所以.
根据上述规定,填空: , , .
15.已知,则 .
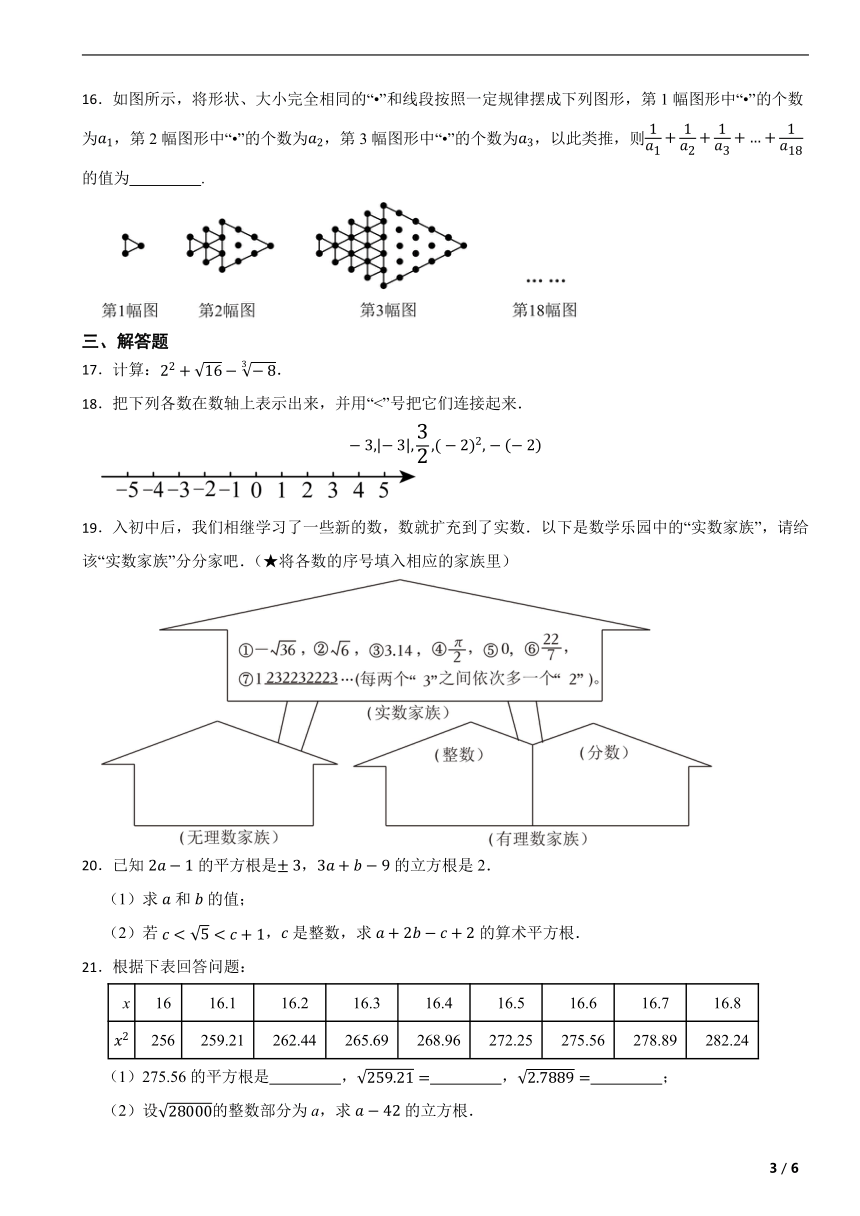
16.如图所示,将形状、大小完全相同的“ ”和线段按照一定规律摆成下列图形,第1幅图形中“ ”的个数为,第2幅图形中“ ”的个数为,第3幅图形中“ ”的个数为,以此类推,则的值为 .
三、解答题
17.计算:.
18.把下列各数在数轴上表示出来,并用“<”号把它们连接起来.
19.入初中后,我们相继学习了一些新的数,数就扩充到了实数.以下是数学乐园中的“实数家族”,请给该“实数家族”分分家吧.(★将各数的序号填入相应的家族里)
20.已知的平方根是,的立方根是2.
(1)求和的值;
(2)若,是整数,求的算术平方根.
21.根据下表回答问题:
x 16 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8
256 259.21 262.44 265.69 268.96 272.25 275.56 278.89 282.24
(1)275.56的平方根是 , , ;
(2)设的整数部分为a,求的立方根.
22.观察下列算式:
①;②;③;④;…
(1)写出第⑥个等式;
(2)猜想第n个等式;(用含n的式子表示)
(3)计算:.
23.材料一:杨辉三角(如图),出现在中国宋朝时期数学家杨辉的著作《详解九章算法》中,是我国数学史上一颗璀璨的明珠,是居于世界前列的数学成就.杨辉三角两腰上的数都是,其余每个数为它的上方(左右)两数之和,揭示了(为非负整数)展开式的项数及各项系数的相关规律,蕴含很多有趣的数学性质,运用规律可以解决很多数学问题.
材料二:斐波那契数列,是意大利数学家莱昂纳多·斐波那契从兔子繁殖问题中引入的一列神奇数字,用表示这一列数中的第个,则数列为,,,,,…,数列从第三项开始,每一项都等于其前两项之和,即(为正整数)
结合材料,回答以下问题:
(1)多项式展开式共有________项,各项系数和为________,利用展开式规律计算:.
(2)我们借助杨辉三角中第三斜行的数:,,,,…记,,,…则;(用表示);.
(3)如图2,把杨辉三角左对齐排列,将同一条斜线上的数字求和,计算可得,,,,,,…若,且,结合材料二,求的值(用k表示).
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】A
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】A
10.【答案】B
11.【答案】3.14
12.【答案】
13.【答案】4
14.【答案】;;
15.【答案】
16.【答案】
17.【答案】
18.【答案】图见解答,
19.【答案】解:
20.【答案】(1),
(2)3
21.【答案】(1);16.1;1.67
(2)解:由.
故.
则,
125的立方根为:5.
22.【答案】(1)解:第⑥个等式为,
(2)解:第个等式为,
(3)解:
=1+2+3+4+……+2023-1
=
.
23.【答案】(1):,,;
(2)36,,;
(3).
1 / 1
一、选择题
1. 2023年9月23日晚,杭州亚运会开幕式现场,超过1.05亿名线上火炬手汇聚而成的“数字火炬手”与现场真实的火炬手一起,共同点燃亚运之火,创造了新的吉尼斯世界纪录.其中数据1.05亿用科学记数法可表示为( )
A. B. C. D.
2.是2023的( )
A.倒数 B.绝对值 C.相反数 D.平方根
3.已知算式的值为0,则“”内应填入的运算符号为( )
A. B. C. D.
4.如表所示的是琳琳作业中的一道题目,“”处都是0但发生破损,琳琳查阅后发现本题答案为1,则破损处“0”的个数为( )
已知:60,求的值
A.4 B.5 C.6 D.7
5.池塘里的睡莲的面积每天长大一倍,若经过13天就可以长满整个池塘,则这些睡莲长满半个池塘需要( )
A.6 B.7 C.10 D.12
6.如图,数轴上的四个点、、、位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB
7.的个位数字为( )
A.1 B.3 C.7 D.9
8.我们把不超过有理数的最大整数称为的整数部分,记作,又把称为的小数部分,记作,则有.如:,,.下列说法中正确的有( )个
①;
②;
③若,且,则或;
④方程的解为或.
A.1 B.2 C.3 D.4
9.法国的“小九九”从“一 一得一”到“五五二十五”和我国的“小九九”是一样的,后面的就改用手势了.下面两个图框是用法国“小九九”计算和的两个示例,且左手伸出的手指数不大于右手伸出的手指数.若用法国的“小九九”计算,左、右手依次伸出手指的个数是( )
?
因为两手伸出的手指数的和为,未伸出的手指数的积为,所以 ?
因为两手伸出的手指数的和为,未伸出的手指数的积为,所以
A., B., C., D.,
10.“幻方”在中国古代称为“河图”、“洛书”,又叫“纵横图”.其主要性质是在一个由若干个排列整齐的数组成的正方形中,图中任意一横行,一纵行及对角线的几个数之和都相等.图(l)所示是一个幻方.有人建议向火星发射如图(2)所示的幻方图案,如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).图(3)是一个未完成的幻方,请你类比图(l)推算图(3)中处所对应的数字是( )
A.1 B.2 C.3 D.4
二、填空题
11.用四舍五入把3.1426精确到百分位,所得到的近似数是 .
12.计算: .
13.数的位置如图,化简 .
14.规定三数a,b,c之间的一种运算:如果,那么.例如:因为,所以.
根据上述规定,填空: , , .
15.已知,则 .
16.如图所示,将形状、大小完全相同的“ ”和线段按照一定规律摆成下列图形,第1幅图形中“ ”的个数为,第2幅图形中“ ”的个数为,第3幅图形中“ ”的个数为,以此类推,则的值为 .
三、解答题
17.计算:.
18.把下列各数在数轴上表示出来,并用“<”号把它们连接起来.
19.入初中后,我们相继学习了一些新的数,数就扩充到了实数.以下是数学乐园中的“实数家族”,请给该“实数家族”分分家吧.(★将各数的序号填入相应的家族里)
20.已知的平方根是,的立方根是2.
(1)求和的值;
(2)若,是整数,求的算术平方根.
21.根据下表回答问题:
x 16 16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8
256 259.21 262.44 265.69 268.96 272.25 275.56 278.89 282.24
(1)275.56的平方根是 , , ;
(2)设的整数部分为a,求的立方根.
22.观察下列算式:
①;②;③;④;…
(1)写出第⑥个等式;
(2)猜想第n个等式;(用含n的式子表示)
(3)计算:.
23.材料一:杨辉三角(如图),出现在中国宋朝时期数学家杨辉的著作《详解九章算法》中,是我国数学史上一颗璀璨的明珠,是居于世界前列的数学成就.杨辉三角两腰上的数都是,其余每个数为它的上方(左右)两数之和,揭示了(为非负整数)展开式的项数及各项系数的相关规律,蕴含很多有趣的数学性质,运用规律可以解决很多数学问题.
材料二:斐波那契数列,是意大利数学家莱昂纳多·斐波那契从兔子繁殖问题中引入的一列神奇数字,用表示这一列数中的第个,则数列为,,,,,…,数列从第三项开始,每一项都等于其前两项之和,即(为正整数)
结合材料,回答以下问题:
(1)多项式展开式共有________项,各项系数和为________,利用展开式规律计算:.
(2)我们借助杨辉三角中第三斜行的数:,,,,…记,,,…则;(用表示);.
(3)如图2,把杨辉三角左对齐排列,将同一条斜线上的数字求和,计算可得,,,,,,…若,且,结合材料二,求的值(用k表示).
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】A
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】A
10.【答案】B
11.【答案】3.14
12.【答案】
13.【答案】4
14.【答案】;;
15.【答案】
16.【答案】
17.【答案】
18.【答案】图见解答,
19.【答案】解:
20.【答案】(1),
(2)3
21.【答案】(1);16.1;1.67
(2)解:由.
故.
则,
125的立方根为:5.
22.【答案】(1)解:第⑥个等式为,
(2)解:第个等式为,
(3)解:
=1+2+3+4+……+2023-1
=
.
23.【答案】(1):,,;
(2)36,,;
(3).
1 / 1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
