浙教版八年级上册 2.2 等腰三角形 课件(共16张PPT)
文档属性
| 名称 | 浙教版八年级上册 2.2 等腰三角形 课件(共16张PPT) | 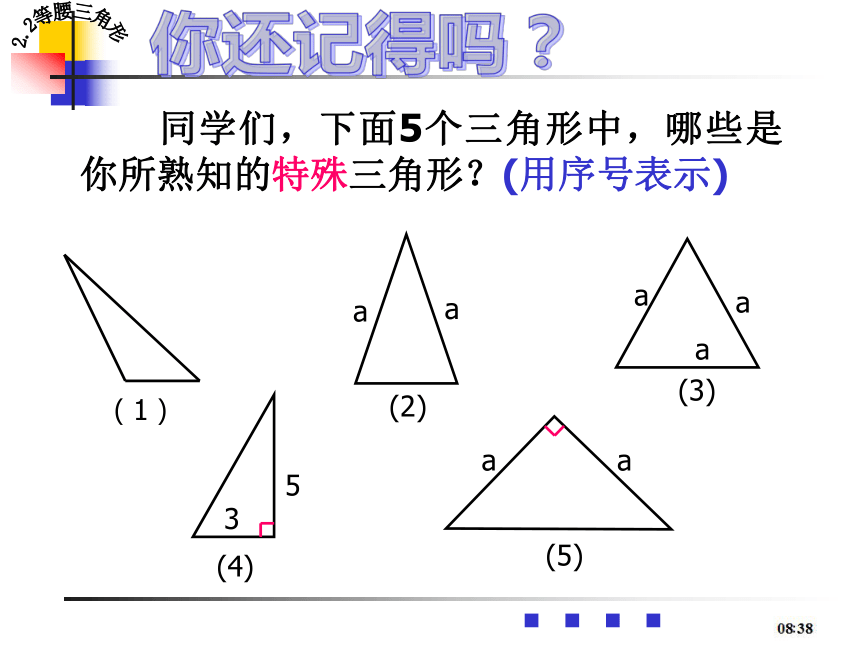 | |
| 格式 | ppt | ||
| 文件大小 | 227.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-30 08:34:31 | ||
图片预览




文档简介
(共17张PPT)
同学们,下面5个三角形中,哪些是你所熟知的特殊三角形?(用序号表示)
(1)
a
a
(2)
a
a
(3)
a
3
5
(4)
a
a
(5)
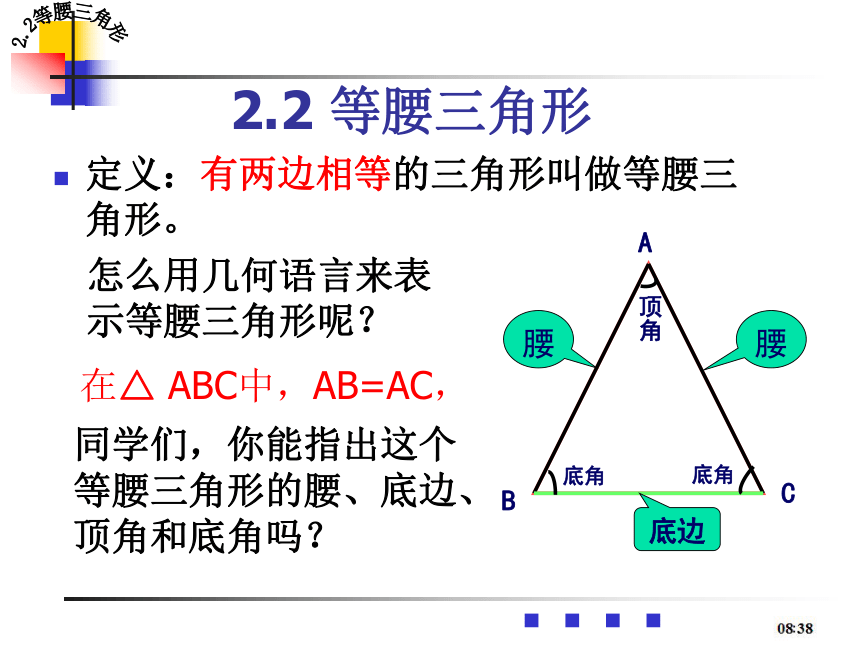
2.2 等腰三角形
定义:有两边相等的三角形叫做等腰三角形。
怎么用几何语言来表示等腰三角形呢?
在△ ABC中,AB=AC,
同学们,你能指出这个等腰三角形的腰、底边、顶角和底角吗?
A
C
B
腰
腰
底边
顶角
底角
底角
同学们,请你先在所给的纸上画一个大大的等腰三角形,然后标上字母,再标出腰、底边、顶角和底角,
完成后,同桌之间互相检查、讨论是否正确。
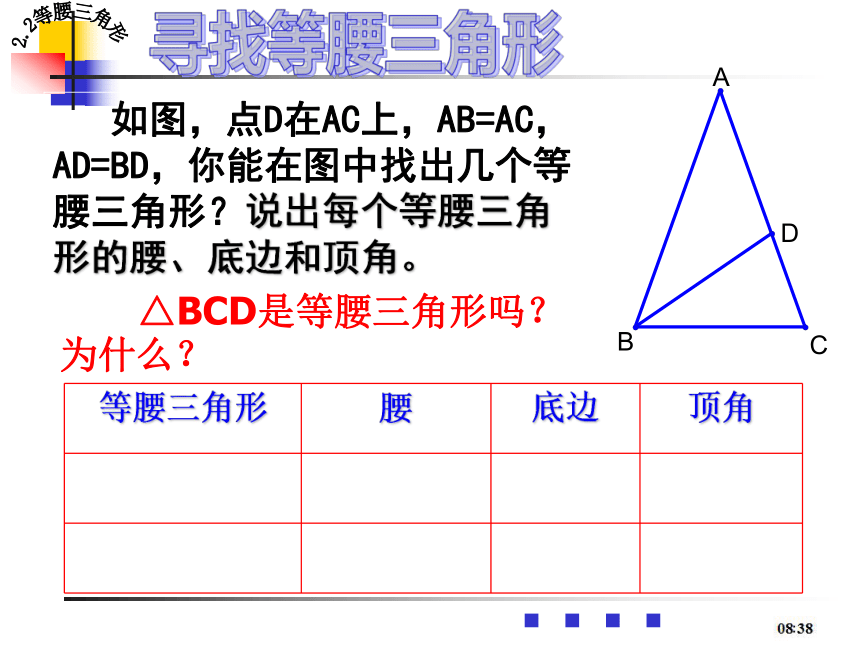
如图,点D在AC上,AB=AC,AD=BD,你能在图中找出几个等腰三角形?说出每个等腰三角形的腰、底边和顶角。
等腰三角形 腰 底边 顶角
△BCD是等腰三角形吗?为什么?
同学们,想一想刚才你们是凭什么来判断同桌所画三角形是等腰三角形的?(可以再重新检查一下)!
度量法
叠合法
折纸
使用圆规
已知线段a,b(如图).用直尺和圆规作等腰三角形ABC,使AB=AC=b,BC=a.
a
b
完成后,同桌之间互相检查、讨论是否正确。
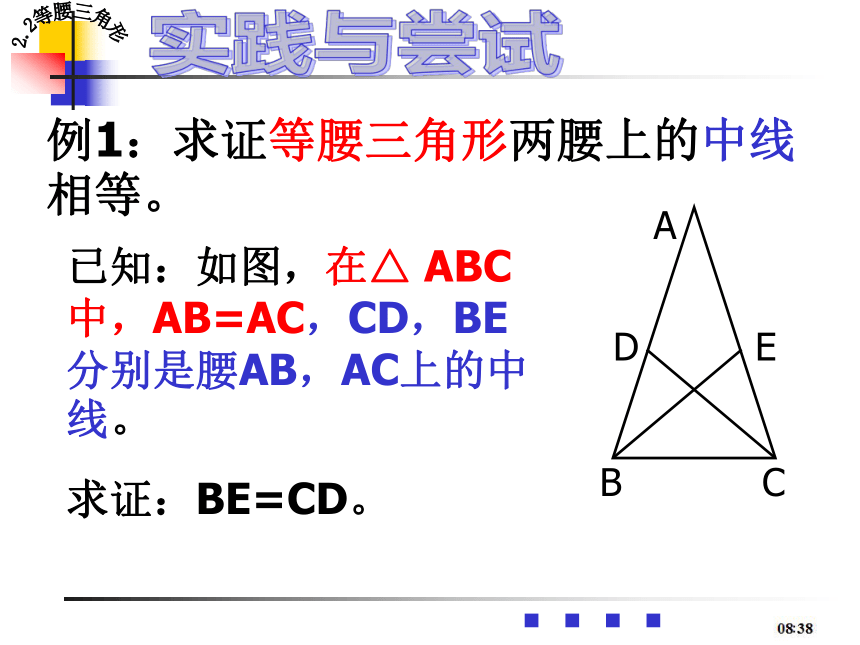
例1:求证等腰三角形两腰上的中线相等。
已知:如图,在△ ABC中,AB=AC,CD,BE分别是腰AB,AC上的中线。
求证:BE=CD。
B
C
D
E
A
1、等腰三角形的两边长分别为2和3,则第三边长为: 。
2、等腰三角形的两边长分别为2和4,则周长为: 。
3、等腰三角形的周长是30,一边长是12,则另两边长是______________
(分类讨论思想)
2或3
10
(要考虑三边关系)
12、6或9、9
同学们拿出刚才的纸,我们进一步来观察,折叠后,除了点B与点C重合外,还有哪些点、线段或角也重合?
顶角平分线所在的直线是它的对称轴。(直线AD)
D
A
B
C
等腰三角形是轴对称图形,
等边三角形有几条对称轴?为什么?
定义:三边都相等的三角形叫做等边三角形。它们是一类特殊的等腰三角形。
等边三角形有三条对称轴。
C
A
等边△ABC
B
同学们请在AB边上任意取一点E,你能作出点E关于AD的对称点F吗?
D
C
B
A
E
H
在AC上取点F,使得AF=AE,则点F即为所求作的点E关于AD的对称点。为什么?
对称点E和F的连线段与AD有什么位置关系?
F
E
B
P
D
C
A
理由如下:∵AP是∠ABC的平分线,AB=AC,AD=AE,
解: 点D,E关于AP对称,且DE∥BC。
∴点B和点C,点D和点E都关于直线AP对称.
∴BC ⊥ AP, DE⊥ AP(为什么?)
∴DE ∥ BC.
∴等腰三角形ABC和等腰三角形ADE都是以直线AP为对称轴的轴对称图形,
例2:如图,在△ABC中,AB=AC,D、E分别是AB,AC上的点,且AD=AE,AP是△ABC的角平分线。点D,E关于AP对称吗?DE与BC有怎样的位置关系?请说明你的判断。
1、等腰三角形的两边长分别为2和3,则第三边长为: 。
2、等腰三角形的两边长分别为2和4,则周长为: 。
4、已知一等腰三角形三边分别为3x-1、
x+1、5,试求x的值。
3、等腰三角形的周长是30,一边长是12,则另两边长是______________
(分类讨论思想)
2或3
10
(要考虑三边关系)
12、6或9、9
2
方程思想
※等腰三角形一腰上的中线将这个等腰三角形的周长分成15cm和6cm两部分,求这个等腰三角形的底边长。
A
B
C
D
BC=1? BC=13?
(舍去)
方程思想
分类讨论思想
AB=10; AB=4
1、等腰三角形、等边三角形的定义及腰、底边、顶角和底角的概念:
2、等腰三角形的轴对称性:
3、解决有关等腰三角形的计算题时,要注意考虑到 思想和 思想。
: 的三角形叫做等腰三角形. 的三角形叫等边三角形.等腰三角形中,相等的两边都叫做 ,第三边叫做 ,两腰的夹角叫做 ,腰和底边的夹角叫做 .
:等腰三角形是 , 所在的直线是它的对称轴,等边三角形有 条对称轴。
作业:
作业本(1) (必做)
P55,作业题5,6 (选做)
同学们,下面5个三角形中,哪些是你所熟知的特殊三角形?(用序号表示)
(1)
a
a
(2)
a
a
(3)
a
3
5
(4)
a
a
(5)
2.2 等腰三角形
定义:有两边相等的三角形叫做等腰三角形。
怎么用几何语言来表示等腰三角形呢?
在△ ABC中,AB=AC,
同学们,你能指出这个等腰三角形的腰、底边、顶角和底角吗?
A
C
B
腰
腰
底边
顶角
底角
底角
同学们,请你先在所给的纸上画一个大大的等腰三角形,然后标上字母,再标出腰、底边、顶角和底角,
完成后,同桌之间互相检查、讨论是否正确。
如图,点D在AC上,AB=AC,AD=BD,你能在图中找出几个等腰三角形?说出每个等腰三角形的腰、底边和顶角。
等腰三角形 腰 底边 顶角
△BCD是等腰三角形吗?为什么?
同学们,想一想刚才你们是凭什么来判断同桌所画三角形是等腰三角形的?(可以再重新检查一下)!
度量法
叠合法
折纸
使用圆规
已知线段a,b(如图).用直尺和圆规作等腰三角形ABC,使AB=AC=b,BC=a.
a
b
完成后,同桌之间互相检查、讨论是否正确。
例1:求证等腰三角形两腰上的中线相等。
已知:如图,在△ ABC中,AB=AC,CD,BE分别是腰AB,AC上的中线。
求证:BE=CD。
B
C
D
E
A
1、等腰三角形的两边长分别为2和3,则第三边长为: 。
2、等腰三角形的两边长分别为2和4,则周长为: 。
3、等腰三角形的周长是30,一边长是12,则另两边长是______________
(分类讨论思想)
2或3
10
(要考虑三边关系)
12、6或9、9
同学们拿出刚才的纸,我们进一步来观察,折叠后,除了点B与点C重合外,还有哪些点、线段或角也重合?
顶角平分线所在的直线是它的对称轴。(直线AD)
D
A
B
C
等腰三角形是轴对称图形,
等边三角形有几条对称轴?为什么?
定义:三边都相等的三角形叫做等边三角形。它们是一类特殊的等腰三角形。
等边三角形有三条对称轴。
C
A
等边△ABC
B
同学们请在AB边上任意取一点E,你能作出点E关于AD的对称点F吗?
D
C
B
A
E
H
在AC上取点F,使得AF=AE,则点F即为所求作的点E关于AD的对称点。为什么?
对称点E和F的连线段与AD有什么位置关系?
F
E
B
P
D
C
A
理由如下:∵AP是∠ABC的平分线,AB=AC,AD=AE,
解: 点D,E关于AP对称,且DE∥BC。
∴点B和点C,点D和点E都关于直线AP对称.
∴BC ⊥ AP, DE⊥ AP(为什么?)
∴DE ∥ BC.
∴等腰三角形ABC和等腰三角形ADE都是以直线AP为对称轴的轴对称图形,
例2:如图,在△ABC中,AB=AC,D、E分别是AB,AC上的点,且AD=AE,AP是△ABC的角平分线。点D,E关于AP对称吗?DE与BC有怎样的位置关系?请说明你的判断。
1、等腰三角形的两边长分别为2和3,则第三边长为: 。
2、等腰三角形的两边长分别为2和4,则周长为: 。
4、已知一等腰三角形三边分别为3x-1、
x+1、5,试求x的值。
3、等腰三角形的周长是30,一边长是12,则另两边长是______________
(分类讨论思想)
2或3
10
(要考虑三边关系)
12、6或9、9
2
方程思想
※等腰三角形一腰上的中线将这个等腰三角形的周长分成15cm和6cm两部分,求这个等腰三角形的底边长。
A
B
C
D
BC=1? BC=13?
(舍去)
方程思想
分类讨论思想
AB=10; AB=4
1、等腰三角形、等边三角形的定义及腰、底边、顶角和底角的概念:
2、等腰三角形的轴对称性:
3、解决有关等腰三角形的计算题时,要注意考虑到 思想和 思想。
: 的三角形叫做等腰三角形. 的三角形叫等边三角形.等腰三角形中,相等的两边都叫做 ,第三边叫做 ,两腰的夹角叫做 ,腰和底边的夹角叫做 .
:等腰三角形是 , 所在的直线是它的对称轴,等边三角形有 条对称轴。
作业:
作业本(1) (必做)
P55,作业题5,6 (选做)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
