浙教版八年级上册 2.5 逆命题和逆定理 课件(共17张PPT)

(共17张PPT)
请同学们准备好数学书、草稿纸、数学工具和一份美丽的心情。
TJBT
Are you ready？
选一个最喜欢的任课老师。
数学老师是最喜欢的老师。
TJBT
数学老师是最喜欢的老师吗？
定义：
一般地，判断某一件事情的句子叫做命题.
结构：
条件：已知事项
结论：由已知事项得到的事项
分类：
真命题
假命题
命题
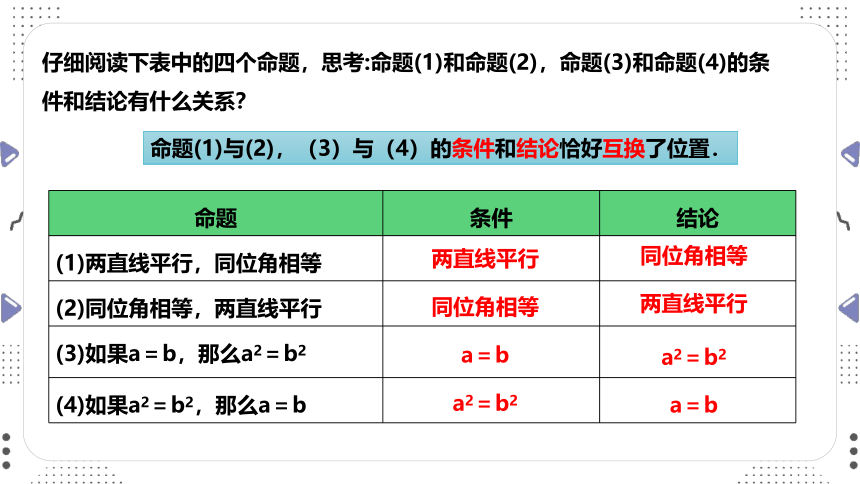
仔细阅读下表中的四个命题，思考:命题(1)和命题(2)，命题(3)和命题(4)的条件和结论有什么关系？
命题 条件 结论
(1)两直线平行，同位角相等
(2)同位角相等，两直线平行
(3)如果a＝b，那么a2＝b2
(4)如果a2＝b2，那么a＝b
a＝b
a2＝b2
a2＝b2
a＝b
两直线平行
同位角相等
同位角相等
两直线平行
命题(1)与(2)，（3）与（4）的条件和结论恰好互换了位置．
2.5逆命题和逆定理
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
新知讲解
逆命题：在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题.
我们把其中的一个叫做原命题，另一个叫做它的逆命题.
例如，命题（1）与命题（2），命题（3）与命题（4）
牛刀小试
（1）长方形有两条对称轴．
（2）磁悬浮列车是一种高速行驶时不接触地面的交通工具．
（3）内错角相等，两直线平行.
(4）对顶角相等.
说出下列命题的逆命题，并判定逆命题的真假：
小技巧
写原命题的逆命题时，可以先将原命题写成“如果 ，那么 ”的形式，再互换条件与结论，进而写出原命题的逆命题.
(5) 等腰三角形的两条腰相等.
新知讲解2
如果一个定理的逆命题能被证明是真命题，那么就叫它是原定理的逆定理，这两个定理叫互逆定理.
等腰三角形的两腰相等 两边相等的三角形是等腰三角形
所有定理都有逆定理吗？
思考
举例？
判断下列说法是否正确？请说明理由。
（1）假命题没有逆命题；
（2）真命题没有逆命题；
（3）每个命题都有逆命题；
（4）真命题的逆命题是真命题；
（5）每个定理都有逆定理；
（6）逆定理有真有假.
牛刀小试2
例题讲解
例1 说出定理“线段垂直平分线上的点到线段两端的距离相等”的逆命题。
解:这个定理的逆命题是:
到线段两端点距离相等的点在线段的垂直平分线上．
A
P
B
已知：如图，AB是一条线段，P是一点，且PA=PB
求证：点P在线段AB的垂直平分线上
作PC⊥AB于点O
O
C
证明:
∵PA=PB，PO⊥AB
∴OA=OB（等腰三角形三线合一性质）
∴PC是AB的垂直平分线
∴点P在线段AB的垂直平分线上
（1）当点P在线段AB上，结论显然成立；
（2）当点P不在线段AB上时
线段垂直平分线性质定理：
到线段两端点距离相等的点，在这条线段的垂直平分线上
A
P
B
几何语言：
∵PA=PB
∴点P在AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
线段垂直平分线性质定理的逆定理：
显然，上述两个定理可称为互逆定理
例2：写出命题“两个全等三角形的面积相等”的逆命题，
判断这个命题的真假，并给出证明.
例题讲解
C
D
A
E
B
F
举反例
牛刀小试3
写出定理“等腰三角形底边上的高线与中线互相重合”的逆命题，并判断这个逆命题的真假.
课堂小结
逆命题
逆命题和逆定理
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
TJBT
逆定理
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
THANK YOU