浙教版八年级上册 2.6 直角三角形 课件(共28张PPT)
文档属性
| 名称 | 浙教版八年级上册 2.6 直角三角形 课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-02 09:55:11 | ||
图片预览




文档简介
(共28张PPT)
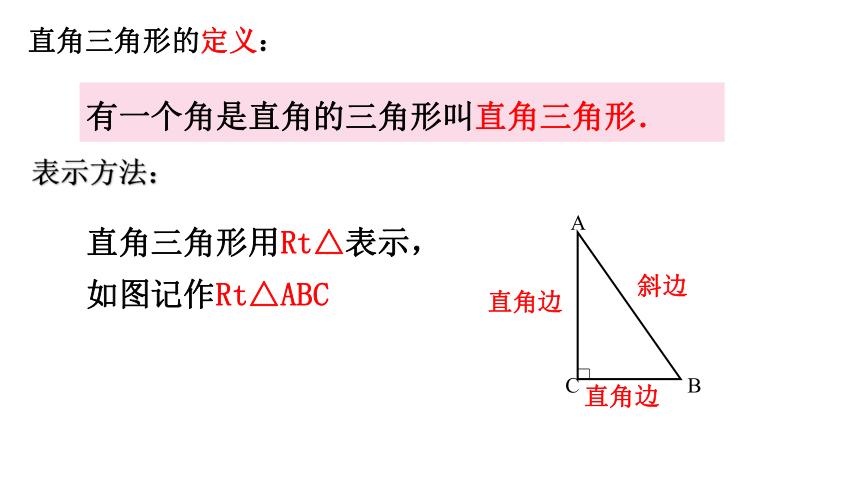
直角三角形用Rt△表示,
如图记作Rt△ABC
A
C
B
直角边
斜边
直角边
有一个角是直角的三角形叫直角三角形.
直角三角形的定义:
表示方法:
A
C
B
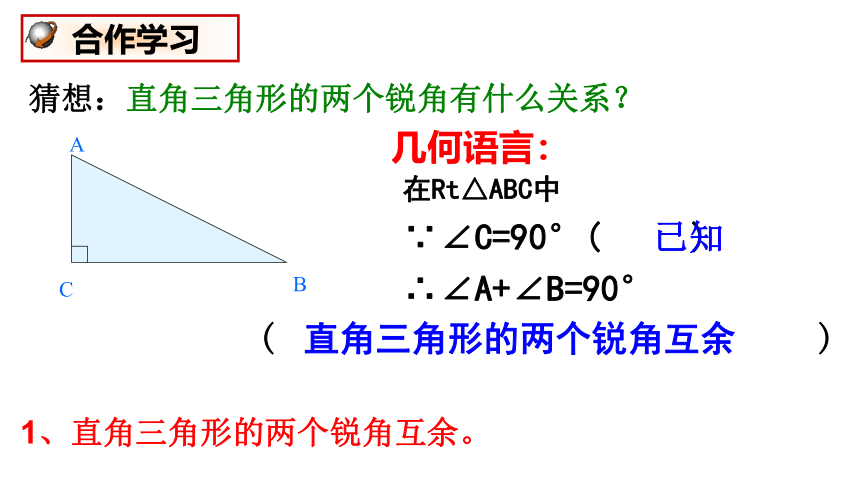
猜想:直角三角形的两个锐角有什么关系?
1、直角三角形的两个锐角互余。
合作学习
几何语言:
在Rt△ABC中
∵∠C=90°( )
已知
∴∠A+∠B=90°
( )
直角三角形的两个锐角互余
1. Rt△ABC中,∠C=Rt∠,
∠B=50°
则∠A=__.
∠B-∠A= 50°
∠A:∠B=3:2
练一练
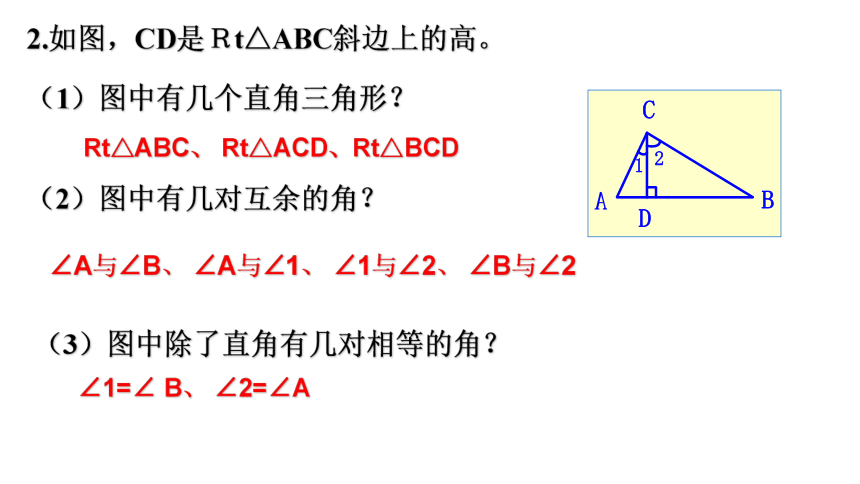
2.如图,CD是Rt△ABC斜边上的高。
(1)图中有几个直角三角形?
Rt△ABC、 Rt△ACD、Rt△BCD
(2)图中有几对互余的角?
∠A与∠B、 ∠A与∠1、 ∠1与∠2、 ∠B与∠2
(3)图中除了直角有几对相等的角?
∠1=∠ B、 ∠2=∠A
勾股定理
即 直角三角形两直角边的平方和等于斜边的平方.
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
在西方又称毕达哥拉斯定理
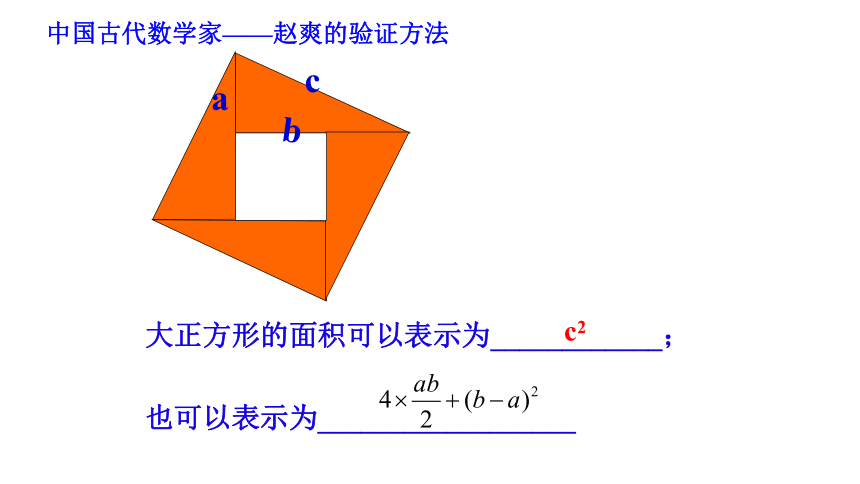
b
c
a
大正方形的面积可以表示为____________;
也可以表示为__________________
c2
中国古代数学家——赵爽的验证方法
1:
已知在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)a=1,b=2,求c
(2)a=15,c =17,求b
定理运用
(3)若a:b=5:12,c=13,求a,b
2、已知直角三角形的两边长分别是3cm和4cm,则第三边的长度为_______.
A
B
40
90
160
40
3:
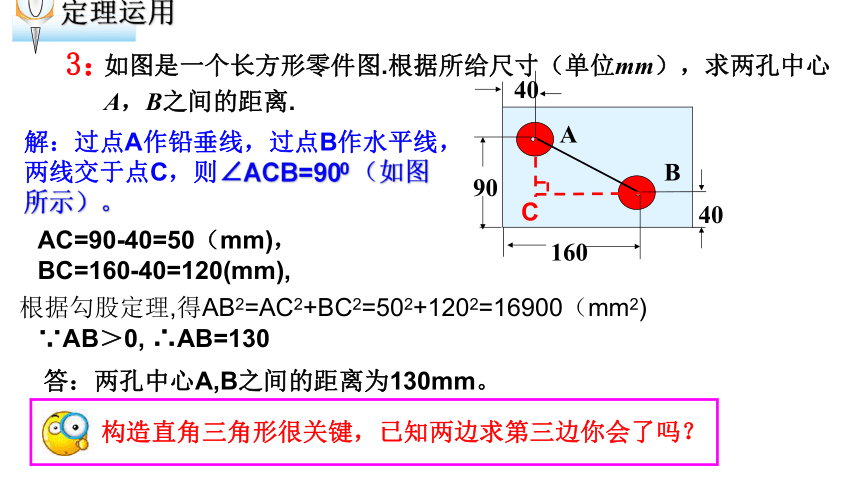
如图是一个长方形零件图.根据所给尺寸(单位mm),求两孔中心A,B之间的距离.
构造直角三角形很关键,已知两边求第三边你会了吗?
定理运用
解:过点A作铅垂线,过点B作水平线,两线交于点C,则∠ACB=900 (如图所示)。
AC=90-40=50(mm),
BC=160-40=120(mm),
根据勾股定理,得AB2=AC2+BC2=502+1202=16900(mm2)
∵AB>0, ∴AB=130
C
答:两孔中心A,B之间的距离为130mm。
4. 如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题.
定理运用
已知:如图,D是Rt△ABC斜边AB上的一点,BD=CD.
求证: AD=CD.
试一试
证明:
∵BD=CD(已知)
∴∠B=∠DCB(在同一个三角形中,等边对等角)
∵∠A+∠B=90°
∠ACD+∠DCB=90°
∴∠A=∠ACD(等角的余角相等)
∴AD=CD(在同一个三角形中,等角对等边)
从本题中,你发现直角三角形斜边上的中线有什么性质?
直角三角形斜边上的中线等于斜边的一半。
直角三角形的性质:
几何语言:
∵ ∠ ACB=900 ,CD是AB边上的中线
∴CD=AD=DB= AB
2、已知△ABC中,∠A=90°,BC=20cm,则BC边上的中线为
7
10cm
1、在Rt△ABC中,CD是斜边AB上的中线,若CD=3.5厘米,则AB=__厘米
练一练
3.如图,AB⊥AC, BD⊥CD,M是BC的中点。
求证:(1)AM=DM;
(2)连结AD,取AD的中点N,连结MN,你能判断MN与AD的位置关系吗?
N
.
AC=6,则CD和AB的长分别为多少?
4、在Rt△ABC中,CD是斜边AB上的中线,∠CDA=80°,
求∠A,∠B的度数.
变式:在Rt△ABC中,CD是斜边AB上的中线,
∠B=30°,求∠DCB,∠ADC的度数.
练一练
例: 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑至B.已知AB=200m,问这名滑雪运动员的高度下降了多少m?
C
解:如图,作AC⊥BC于点C,
D
取AB的中点D,连结CD
∵Rt△ABC,且D为AB上的中点
∵∠B=30°,∠ACB=90°
∴CD=BD=AD= AB= ×200=100
∴∠A=90°- 30°=60°
∴△ADC为等边三角形
∴AC=AD=100m
直角三角形中30°所对的直角边是斜边的一半 。
练习1 、如图,在△ABC中,∠C=900,∠B=150,DE是AB的中垂线,BE=5,则AE=______,AC=_____
E
D
A
C
B
5
2.5
2. AB=AC=5米。D是AB的中点,AE⊥BC。如果∠BAC=120゜, 求AE和DE的长度。
2、用刻度尺和圆规,作一条线段,使它的长度为 cm.
如何构造直角三角形是关键,数形结合思想很重要
1、直角三角形的两直角边为6和8,则斜边上的中线为___;斜边上的高线为___
练一练
3、如图,在△ABC中, ∠ACB=900,CD⊥AB于D, ∠A=300,则AD的值为( )
A. 4BD B. 3BD C. 2BD D. BD
4. 在《九章算术》中记载了一道有趣的数学题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”这道题的意思是说:有一个边长为1丈的正方形水池,在池的中央长着一根芦苇,芦苇露出水面1尺。若将芦苇拉到池边中点处,芦苇的顶端恰好到达水面。问水有多深?芦苇有多长?
x
X+1
设水深x尺,则芦苇长(x+1)尺,
X2+52=(x+1)2
求下列图中数与字母所代表的正方形面积:
10
15
A
6
25
B
=25
=19
A
B
C
D
7cm
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___cm2。
49
合作探究:
思维拓展:
1、在△ABC中,AB=AC=10,∠C=750, 则△ABC的面积为______.
25
2、如图,已知Rt△ABC中,∠C=900,∠A=300,AC=10,沿DE折叠,使得点A与点B重合,则折痕DE的长为_______.
上图中的三角板所表示的三角形有什么特征?
等腰直角三角形
两条直角边相等的直角三角形叫做等腰直角三角形。
A
C
B
它有什么性质呢?
2)具有直角三角形的所有性质
1)具有等腰三角形的所有性质
D
结论:斜边上的高把等腰直角三角形分为两个全等的等腰直角三角形。
3、如图,在△ABC中,AD ⊥BC,DE、DF分别是AC、AB边上的中线。
(1)若AB=AC,则△DEF是什么形状的三角形?
(2)请补充一个条件,使△DEF为等腰直角三角形。
E
F
D
A
B
C
拓展提高:
1. 直角三角形的定义和表示
2.直角三角形的两个锐角互余.
3.直角三角形斜边上的中线等于斜边的一半
直角三角形用Rt△表示,
如图记作Rt△ABC
A
C
B
直角边
斜边
直角边
有一个角是直角的三角形叫直角三角形.
直角三角形的定义:
表示方法:
A
C
B
猜想:直角三角形的两个锐角有什么关系?
1、直角三角形的两个锐角互余。
合作学习
几何语言:
在Rt△ABC中
∵∠C=90°( )
已知
∴∠A+∠B=90°
( )
直角三角形的两个锐角互余
1. Rt△ABC中,∠C=Rt∠,
∠B=50°
则∠A=__.
∠B-∠A= 50°
∠A:∠B=3:2
练一练
2.如图,CD是Rt△ABC斜边上的高。
(1)图中有几个直角三角形?
Rt△ABC、 Rt△ACD、Rt△BCD
(2)图中有几对互余的角?
∠A与∠B、 ∠A与∠1、 ∠1与∠2、 ∠B与∠2
(3)图中除了直角有几对相等的角?
∠1=∠ B、 ∠2=∠A
勾股定理
即 直角三角形两直角边的平方和等于斜边的平方.
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
在西方又称毕达哥拉斯定理
b
c
a
大正方形的面积可以表示为____________;
也可以表示为__________________
c2
中国古代数学家——赵爽的验证方法
1:
已知在△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)a=1,b=2,求c
(2)a=15,c =17,求b
定理运用
(3)若a:b=5:12,c=13,求a,b
2、已知直角三角形的两边长分别是3cm和4cm,则第三边的长度为_______.
A
B
40
90
160
40
3:
如图是一个长方形零件图.根据所给尺寸(单位mm),求两孔中心A,B之间的距离.
构造直角三角形很关键,已知两边求第三边你会了吗?
定理运用
解:过点A作铅垂线,过点B作水平线,两线交于点C,则∠ACB=900 (如图所示)。
AC=90-40=50(mm),
BC=160-40=120(mm),
根据勾股定理,得AB2=AC2+BC2=502+1202=16900(mm2)
∵AB>0, ∴AB=130
C
答:两孔中心A,B之间的距离为130mm。
4. 如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题.
定理运用
已知:如图,D是Rt△ABC斜边AB上的一点,BD=CD.
求证: AD=CD.
试一试
证明:
∵BD=CD(已知)
∴∠B=∠DCB(在同一个三角形中,等边对等角)
∵∠A+∠B=90°
∠ACD+∠DCB=90°
∴∠A=∠ACD(等角的余角相等)
∴AD=CD(在同一个三角形中,等角对等边)
从本题中,你发现直角三角形斜边上的中线有什么性质?
直角三角形斜边上的中线等于斜边的一半。
直角三角形的性质:
几何语言:
∵ ∠ ACB=900 ,CD是AB边上的中线
∴CD=AD=DB= AB
2、已知△ABC中,∠A=90°,BC=20cm,则BC边上的中线为
7
10cm
1、在Rt△ABC中,CD是斜边AB上的中线,若CD=3.5厘米,则AB=__厘米
练一练
3.如图,AB⊥AC, BD⊥CD,M是BC的中点。
求证:(1)AM=DM;
(2)连结AD,取AD的中点N,连结MN,你能判断MN与AD的位置关系吗?
N
.
AC=6,则CD和AB的长分别为多少?
4、在Rt△ABC中,CD是斜边AB上的中线,∠CDA=80°,
求∠A,∠B的度数.
变式:在Rt△ABC中,CD是斜边AB上的中线,
∠B=30°,求∠DCB,∠ADC的度数.
练一练
例: 如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A滑至B.已知AB=200m,问这名滑雪运动员的高度下降了多少m?
C
解:如图,作AC⊥BC于点C,
D
取AB的中点D,连结CD
∵Rt△ABC,且D为AB上的中点
∵∠B=30°,∠ACB=90°
∴CD=BD=AD= AB= ×200=100
∴∠A=90°- 30°=60°
∴△ADC为等边三角形
∴AC=AD=100m
直角三角形中30°所对的直角边是斜边的一半 。
练习1 、如图,在△ABC中,∠C=900,∠B=150,DE是AB的中垂线,BE=5,则AE=______,AC=_____
E
D
A
C
B
5
2.5
2. AB=AC=5米。D是AB的中点,AE⊥BC。如果∠BAC=120゜, 求AE和DE的长度。
2、用刻度尺和圆规,作一条线段,使它的长度为 cm.
如何构造直角三角形是关键,数形结合思想很重要
1、直角三角形的两直角边为6和8,则斜边上的中线为___;斜边上的高线为___
练一练
3、如图,在△ABC中, ∠ACB=900,CD⊥AB于D, ∠A=300,则AD的值为( )
A. 4BD B. 3BD C. 2BD D. BD
4. 在《九章算术》中记载了一道有趣的数学题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”这道题的意思是说:有一个边长为1丈的正方形水池,在池的中央长着一根芦苇,芦苇露出水面1尺。若将芦苇拉到池边中点处,芦苇的顶端恰好到达水面。问水有多深?芦苇有多长?
x
X+1
设水深x尺,则芦苇长(x+1)尺,
X2+52=(x+1)2
求下列图中数与字母所代表的正方形面积:
10
15
A
6
25
B
=25
=19
A
B
C
D
7cm
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___cm2。
49
合作探究:
思维拓展:
1、在△ABC中,AB=AC=10,∠C=750, 则△ABC的面积为______.
25
2、如图,已知Rt△ABC中,∠C=900,∠A=300,AC=10,沿DE折叠,使得点A与点B重合,则折痕DE的长为_______.
上图中的三角板所表示的三角形有什么特征?
等腰直角三角形
两条直角边相等的直角三角形叫做等腰直角三角形。
A
C
B
它有什么性质呢?
2)具有直角三角形的所有性质
1)具有等腰三角形的所有性质
D
结论:斜边上的高把等腰直角三角形分为两个全等的等腰直角三角形。
3、如图,在△ABC中,AD ⊥BC,DE、DF分别是AC、AB边上的中线。
(1)若AB=AC,则△DEF是什么形状的三角形?
(2)请补充一个条件,使△DEF为等腰直角三角形。
E
F
D
A
B
C
拓展提高:
1. 直角三角形的定义和表示
2.直角三角形的两个锐角互余.
3.直角三角形斜边上的中线等于斜边的一半
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
