浙教版八年级上册 2.8 直角三角形全等的判定 课件(共30张PPT)
文档属性
| 名称 | 浙教版八年级上册 2.8 直角三角形全等的判定 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 417.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-02 09:59:24 | ||
图片预览






文档简介
(共30张PPT)
SSS
SAS
ASA
AAS
我们学过的判定三角形全等的方法?
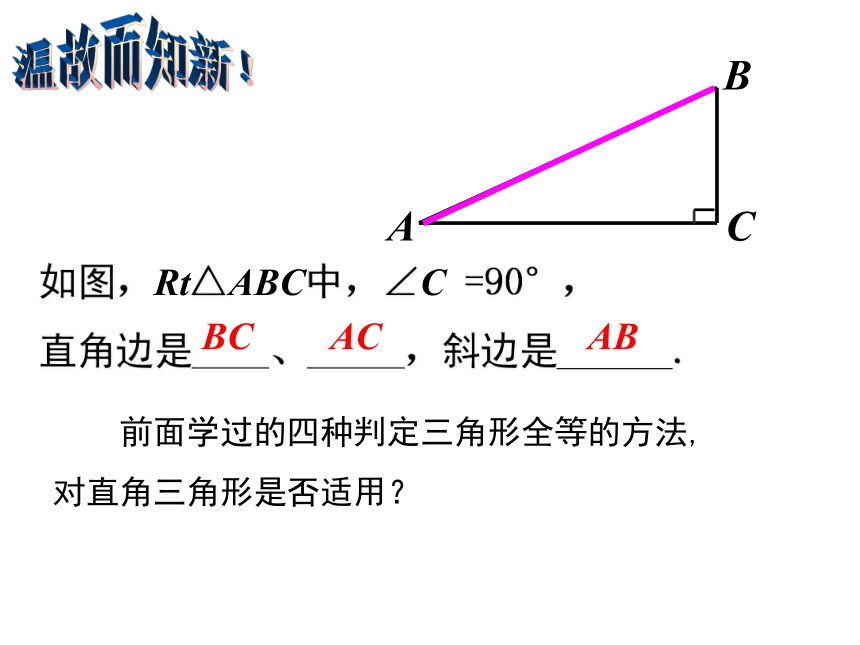
温故而知新!
如图,Rt△ABC中,∠C =90°,
直角边是____、_____,斜边是______.
C
B
A
AC
BC
AB
前面学过的四种判定三角形全等的方法,
对直角三角形是否适用?
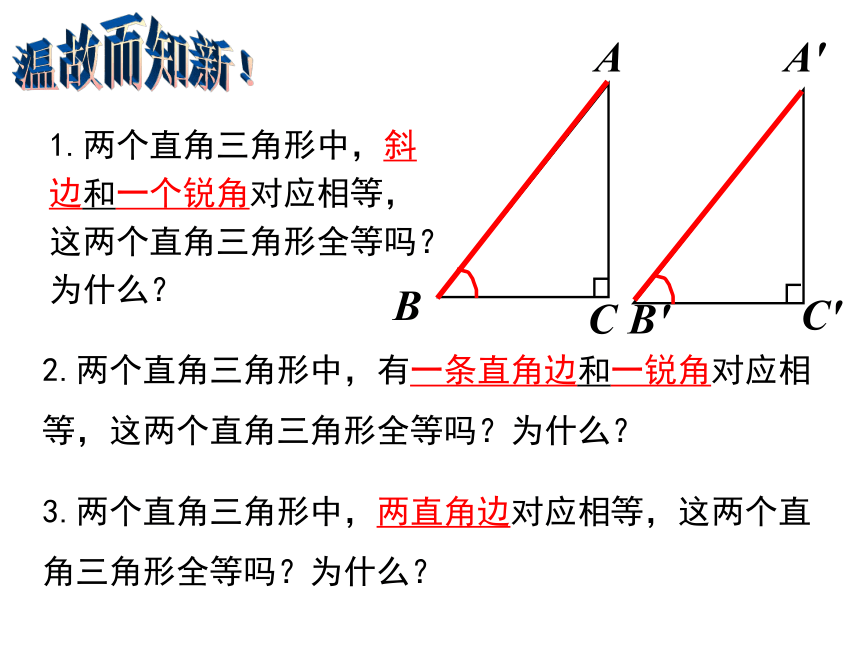
温故而知新!
A
B
C
A′
B′
C′
1.两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
3.两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
温故而知新!
如图,已知AC=DF,BC=EF,
∠B=∠E,△ABC≌△DEF吗?
我们知道,证明三角形全等不存
在SSA定理.
A
B
C
D
E
F
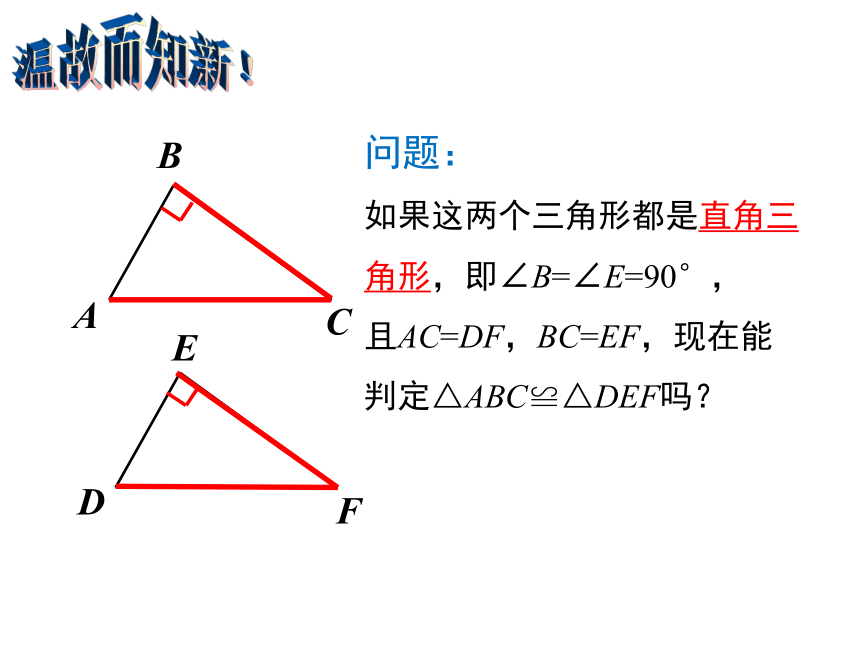
温故而知新!
问题:
如果这两个三角形都是直角三
角形,即∠B=∠E=90°,
且AC=DF,BC=EF,现在能
判定△ABC≌△DEF吗?
A
B
C
D
E
F
1
温故而知新!
任意画出一个Rt△ABC,使∠C=90°。再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
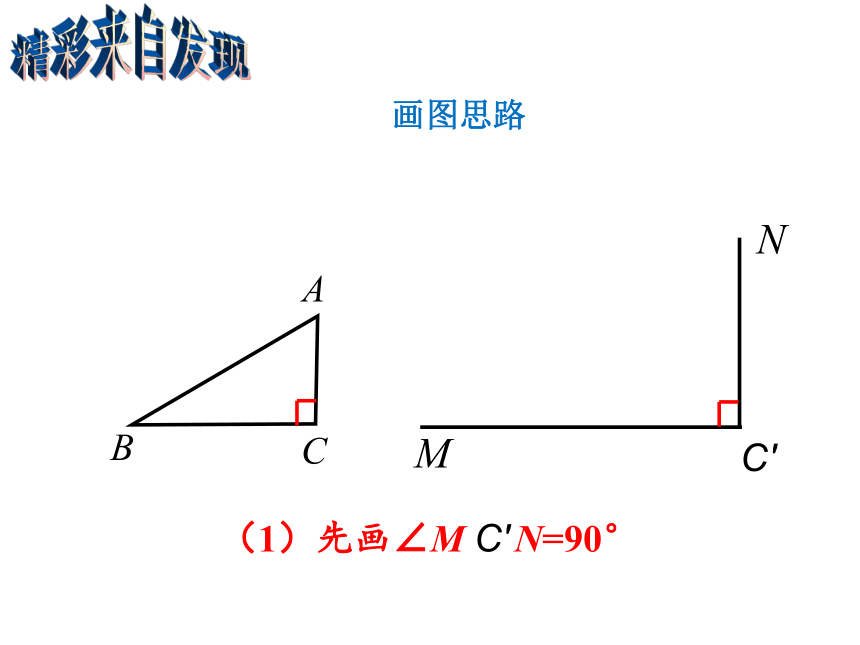
作图探究
精彩来自发现
画图思路
(1)先画∠M C′ N=90°
A
B
C
M
C′
N
精彩来自发现
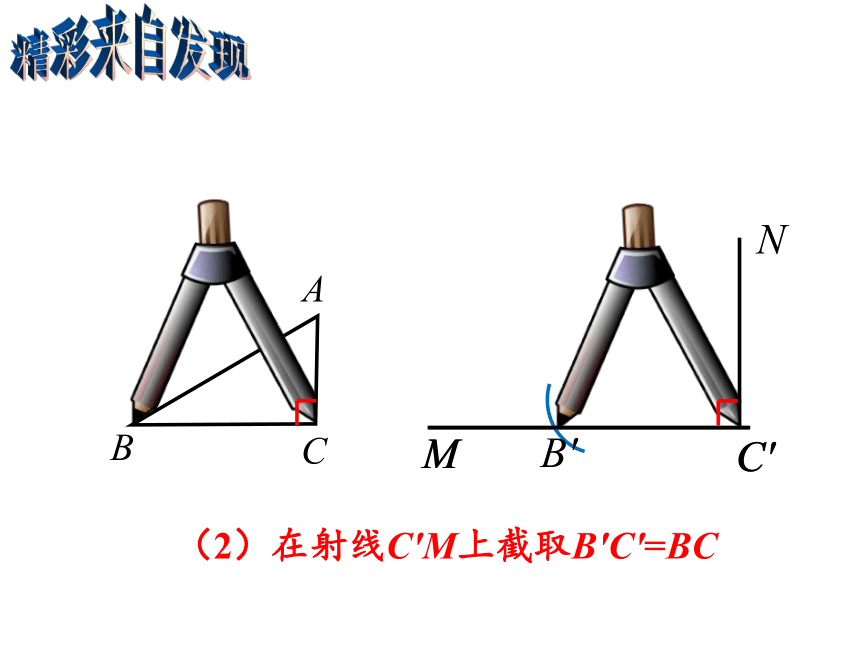
(2)在射线C′M上截取B′C′=BC
M
C′
A
B
C
N
B′
M
C′
精彩来自发现
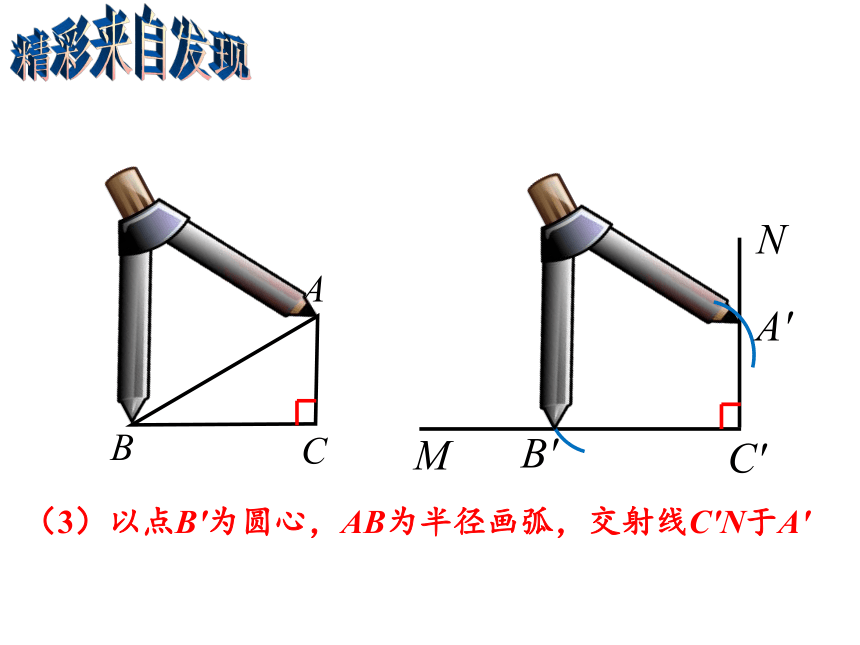
(3)以点B′为圆心,AB为半径画弧,交射线C′N于A′
M
C′
A
B
C
N
B′
A′
精彩来自发现
(4)连接A′B′
M
C′
A
B
C
N
B′
A′
思考:通过上面的探究,你能得出什么结论?
精彩来自发现
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
精彩来自发现
第2章 特殊三角形
2.8 直角三角形全等的判定
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由.
(1)一个锐角和这个角的对边对应相等.( )
(2)一个锐角和这个角的邻边对应相等.( )
(3)一个锐角和斜边对应相等. ( )
(4)两直角边对应相等. ( )
(5)一条直角边和斜边对应相等. ( )
HL
×
SAS
AAS
AAS
试一试,我能行!
例1 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C与∠D都是直角.
AB=BA,
AC=BD ,
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
A
B
D
C
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
典型例题
变式1: 如图, ∠ACB =∠ADB=90,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
A
B
D
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
典型例题
如图,AC、BD相交于点P,AC⊥BC,BD⊥AD,垂足分别为C、D,AD=BC.
求证:AC=BD.
变式2
HL
AC=BD
Rt△ABD≌Rt△BAC
典型例题
例2 如图,已知AD、AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD、AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
典型例题
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
例3:如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF ,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF.
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
典型例题
P
A
O
B
C
D
E
角的内部到角的两边距离相等的点在角的平分线上.
问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
∵ OC平分∠AOB,
且PD⊥OA, PE⊥OB ,
∴ PD= PE.
几何语言:
猜想:
思考:这个结论正确吗?
精彩来自发现
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.求证:点P在∠AOB的角平分线上.
证明:
作射线OP,
∴点P在∠AOB 的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP,
PD= PE,
B
A
D
O
P
E
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°.
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
证明猜想
精彩来自发现
性质定理的逆定理:
角的内部到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
应用格式:
∵ PD⊥OA,PE⊥OB,PD=PE.
∴点P 在∠AOB的平分线上.
精彩来自发现
例4:如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20 000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
O
方法点拨:根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.
典型例题
1. 如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
试一试,我能行!
A
F
C
E
D
B
2.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.
求证:BF=DE.
试一试,我能行!
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BD平分EF.
A
F
C
E
D
B
G
变式训练1
AB=CD,
AF=CE.
Rt△ABF≌Rt△CDE(HL).
BF=DE
Rt△GBF≌Rt△GDE(AAS).
∠BFG=∠DEG
∠BGF=∠DGE
FG=EG
BD平分EF
随堂即练
试一试,我能行!
如图,AB=CD,BF⊥AC,DE⊥AC,AE=CF.想想:BD平分EF吗
变式训练2
C
AB=CD,
AF=CE.
Rt△ABF≌Rt△CDE(HL).
BF=DE
Rt△GBF≌Rt△GDE(AAS).
∠BFG=∠DEG
∠BGF=∠DGE
FG=EG
BD平分EF
随堂即练
试一试,我能行!
如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等?
分析:本题要分情况讨论:(1)Rt△APQ≌Rt△CBA,此时AP=BC=5cm,可据此求出P点的位置.(2)Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm.
头脑风暴
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,
PQ=AB,AP=AC,
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm.
故当AP=5cm或10cm时,△ABC才能和△APQ全等.
方法总结:判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
随堂即练
直角三角形全等的判定
内容
斜边和一条直角边对应相等的两个直角三角形全等
前提条件
在直角三角形中
角平分线
性质定理的逆定理
角的内部到角两边距离相等的点在这个角的平分线上
课堂小结
SSS
SAS
ASA
AAS
我们学过的判定三角形全等的方法?
温故而知新!
如图,Rt△ABC中,∠C =90°,
直角边是____、_____,斜边是______.
C
B
A
AC
BC
AB
前面学过的四种判定三角形全等的方法,
对直角三角形是否适用?
温故而知新!
A
B
C
A′
B′
C′
1.两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
2.两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
3.两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
温故而知新!
如图,已知AC=DF,BC=EF,
∠B=∠E,△ABC≌△DEF吗?
我们知道,证明三角形全等不存
在SSA定理.
A
B
C
D
E
F
温故而知新!
问题:
如果这两个三角形都是直角三
角形,即∠B=∠E=90°,
且AC=DF,BC=EF,现在能
判定△ABC≌△DEF吗?
A
B
C
D
E
F
1
温故而知新!
任意画出一个Rt△ABC,使∠C=90°。再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
作图探究
精彩来自发现
画图思路
(1)先画∠M C′ N=90°
A
B
C
M
C′
N
精彩来自发现
(2)在射线C′M上截取B′C′=BC
M
C′
A
B
C
N
B′
M
C′
精彩来自发现
(3)以点B′为圆心,AB为半径画弧,交射线C′N于A′
M
C′
A
B
C
N
B′
A′
精彩来自发现
(4)连接A′B′
M
C′
A
B
C
N
B′
A′
思考:通过上面的探究,你能得出什么结论?
精彩来自发现
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
精彩来自发现
第2章 特殊三角形
2.8 直角三角形全等的判定
判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由.
(1)一个锐角和这个角的对边对应相等.( )
(2)一个锐角和这个角的邻边对应相等.( )
(3)一个锐角和斜边对应相等. ( )
(4)两直角边对应相等. ( )
(5)一条直角边和斜边对应相等. ( )
HL
×
SAS
AAS
AAS
试一试,我能行!
例1 如图,AC⊥BC, BD⊥AD, AC﹦BD,求证:BC﹦AD.
证明: ∵ AC⊥BC, BD⊥AD, ∴∠C与∠D都是直角.
AB=BA,
AC=BD ,
在 Rt△ABC 和Rt△BAD 中,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
A
B
D
C
应用“HL”的前提条件是在直角三角形中.
这是应用“HL”判定方法的书写格式.
利用全等证明两条线段相等,这是常见的思路.
典型例题
变式1: 如图, ∠ACB =∠ADB=90,要证明△ABC≌ △BAD,还需一个什么条件?把这些条件都写出来,并在相应的括号内填写出判定它们全等的理由.
(1) ( )
(2) ( )
(3) ( )
(4) ( )
A
B
D
C
AD=BC
∠ DAB= ∠ CBA
BD=AC
∠ DBA= ∠ CAB
HL
HL
AAS
AAS
典型例题
如图,AC、BD相交于点P,AC⊥BC,BD⊥AD,垂足分别为C、D,AD=BC.
求证:AC=BD.
变式2
HL
AC=BD
Rt△ABD≌Rt△BAC
典型例题
例2 如图,已知AD、AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
证明:∵AD、AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD-CD=BF-EF.即BC=BE.
典型例题
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
例3:如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF ,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF.
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
典型例题
P
A
O
B
C
D
E
角的内部到角的两边距离相等的点在角的平分线上.
问题:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
∵ OC平分∠AOB,
且PD⊥OA, PE⊥OB ,
∴ PD= PE.
几何语言:
猜想:
思考:这个结论正确吗?
精彩来自发现
已知:如图,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=PE.求证:点P在∠AOB的角平分线上.
证明:
作射线OP,
∴点P在∠AOB 的平分线上.
在Rt△PDO和Rt△PEO 中,
(全等三角形的对应角相等).
OP=OP,
PD= PE,
B
A
D
O
P
E
∵PD⊥OA,PE⊥OB.
∴∠PDO=∠PEO=90°.
∴Rt△PDO≌Rt△PEO( HL).
∴∠AOP=∠BOP
证明猜想
精彩来自发现
性质定理的逆定理:
角的内部到角的两边的距离相等的点在角的平分线上.
P
A
O
B
C
D
E
应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
定理的作用:判断点是否在角平分线上.
应用格式:
∵ PD⊥OA,PE⊥OB,PD=PE.
∴点P 在∠AOB的平分线上.
精彩来自发现
例4:如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500米,这个集贸市场应建在何处(比例尺为1︰20 000)?
D
C
S
解:作夹角的角平分线OC,
截取OD=2.5cm ,D即为所求.
O
方法点拨:根据角平分线的判定定理,要求作的点到两边的距离相等,一般需作这两边直线形成的角的平分线,再在这条角平分线上根据要求取点.
典型例题
1. 如图,某个居民小区C附近有三条两两相交的道路MN、OA、OB,拟在MN上建造一个大型超市,使得它到OA、OB的距离相等,请确定该超市的位置P.
小区C
P
A
O
B
M
N
试一试,我能行!
A
F
C
E
D
B
2.如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.
求证:BF=DE.
试一试,我能行!
如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BD平分EF.
A
F
C
E
D
B
G
变式训练1
AB=CD,
AF=CE.
Rt△ABF≌Rt△CDE(HL).
BF=DE
Rt△GBF≌Rt△GDE(AAS).
∠BFG=∠DEG
∠BGF=∠DGE
FG=EG
BD平分EF
随堂即练
试一试,我能行!
如图,AB=CD,BF⊥AC,DE⊥AC,AE=CF.想想:BD平分EF吗
变式训练2
C
AB=CD,
AF=CE.
Rt△ABF≌Rt△CDE(HL).
BF=DE
Rt△GBF≌Rt△GDE(AAS).
∠BFG=∠DEG
∠BGF=∠DGE
FG=EG
BD平分EF
随堂即练
试一试,我能行!
如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等?
分析:本题要分情况讨论:(1)Rt△APQ≌Rt△CBA,此时AP=BC=5cm,可据此求出P点的位置.(2)Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
解:(1)当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),
∴AP=BC=5cm.
头脑风暴
(2)当P运动到与C点重合时,AP=AC.
在Rt△ABC与Rt△QPA中,
PQ=AB,AP=AC,
∴Rt△QAP≌Rt△BCA(HL),
∴AP=AC=10cm.
故当AP=5cm或10cm时,△ABC才能和△APQ全等.
方法总结:判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
随堂即练
直角三角形全等的判定
内容
斜边和一条直角边对应相等的两个直角三角形全等
前提条件
在直角三角形中
角平分线
性质定理的逆定理
角的内部到角两边距离相等的点在这个角的平分线上
课堂小结
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
