浙教版九年级上册 3.2 图形的旋转 课件(共24张PPT)
文档属性
| 名称 | 浙教版九年级上册 3.2 图形的旋转 课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-02 10:04:41 | ||
图片预览








文档简介
(共24张PPT)
浙教版九(上)§第三章
3.2 图形的旋转
上面的运动现象中,有哪些共同的特点
想一想
绕同一个固定的点,按同一个方向,旋转同一个角度。
叙述一个旋转变换要注意旋转变换的三个要素:
1、旋转中心;
2、旋转的方向;
3、旋转的角度。
由一个图形变为另一个图形,在运动的过程中,原图形上的所有点都绕一个固定的点,按同一个方向,转动同一个角度,这样的图形运动叫做图形的旋转.这个固定的点叫做旋转中心。
什么是旋转
1、如图,经过怎样的旋转变换,可由射线OP得到射线OQ?
O
P
Q
答:将射线OP以O为旋转中心,按顺时针方向,
旋转90°得到射线OQ
说一说
2、本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
说一说
3.下列现象中属于旋转的有( )个
①地下水位逐年下降;②滑雪运动员在雪地上滑行;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
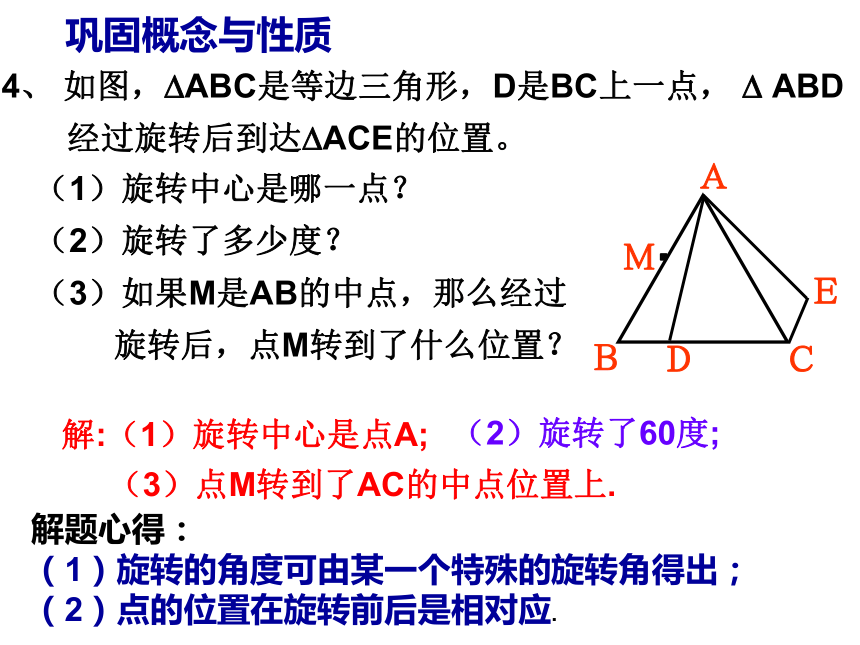
4、 如图, ABC是等边三角形,D是BC上一点, ABD
经过旋转后到达 ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过
旋转后,点M转到了什么位置?
E
D
C
B
A
M
.
解:(1)旋转中心是点A;
(2)旋转了60度;
(3)点M转到了AC的中点位置上.
解题心得:
(1)旋转的角度可由某一个特殊的旋转角得出;
(2)点的位置在旋转前后是相对应.
巩固概念与性质
若叶片 A 绕 O 顺时针旋转到叶片 B,则旋转中心是______,旋转角是_________,旋转角等于____度,其中的对应点有_______、 _______、 _______、 _______、 _______、 _______ 。
A
B
C
D
E
F
O
抢答
O
∠AOB
60
F与A
A与B
B与C
C与D
D与E
E与F
杠杆绕支点转动撬起重物,杠杆的旋转中心就____,旋转角是_______________________。
B
O
B′
A
A′
∠AOA′
O
∠BOB′
或
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
1.旋转中心是什么?
2.经过旋转,点A,B, C
分别移动到什么位置?
3.AO与DO的长有什么关
系?BO与EO呢?
4.∠AOD与∠BOE有什
么大小关系? ∠COF呢?
说一说
(1)旋转不改变图形的形状和大小.
旋转变换的性质
(2)对应点到旋转中心的距离相等,对应点与
旋转中心的连线所成的角度等于旋转的角度.
1、如图,以点O为旋转中心,将点A按逆时针方向
旋转60°,作出经旋转变换后所得的图形。
2、如图,以点O为旋转中心,将线段AB按逆时针
方向旋转60°,作出经旋转变换后所得的图形
O
A
A
B
O
旋转变换的画图
例1、如图,O是△ABC外一点,以点O为旋转中心,
将△ABC按顺时针方向旋转60°,作出经旋转
变换后的像。
.
O
A
B
C
旋转变换的画图
如图,△ ABC绕点C旋转后,顶点A的对应点为点D。试确定顶点B对应点的位置,以及旋转后的三角形。
△DEC就是△ABC绕C点旋转变换后的像.
A
B
D
C
·
E
旋转变换的画图
1:如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
2.如图3-2-1所示,∠AOB=90°,∠B=30°,△A′OB′可以看作是由△AOB绕点O逆时针旋转α角度得到的.若点A′在AB上,则旋转角α的大小可以是
( )
图3-2-1
C
A.30° B.45°
C.60° D.90°
3.如图3-2-2所示,两个全等的正方形ABCD与CDEF,旋转正方形ABCD能和正方形CDEF重合,则可以作为旋转中心的点有______个.
图3-2-2
3
类型之一 旋转及其性质
例3 如图3-2-4所示,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
图3-2-4
(1)线段OA1的长是______.∠AOB1的度数是________;
(2)连结AA1,求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
6
135°
1.如图3-2-10,已知D为等边△ABC内一点,将△DBC绕点C旋转到△EAC的位置.试判断△CDE的形状,并证明你的结论.
图3-2-10
2.如图3-2-6,Rt△ABC是等腰三角形,D是Rt△ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠ADD′的度数是
( )
图3-2-6
D
A.25° B.30°
C.35° D.45°
3.如图3-2-11,把正方形ABCD绕点A按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.求证:HG=HB.
图3-2-11
1、相同:都是一种运动;运动前 后不改变图形的形状和大小
2、不同
形状 大小 方向
轴对称 不变 不变 改变
平移 不变 不变 不变
旋转 不变 不变 改变
3
方法一、先将牌A右下角顶点为旋转中心,将牌A按顺时针方向旋转90°,再向下作一次平移变换,就得到牌B.
方法二、先将牌A向下作一次平移变换,平移到牌A的右下角与牌B的左下角重合,再以牌A的右下角顶点为旋转中心,按顺时针方向旋转90°,再就得到牌B.
浙教版九(上)§第三章
3.2 图形的旋转
上面的运动现象中,有哪些共同的特点
想一想
绕同一个固定的点,按同一个方向,旋转同一个角度。
叙述一个旋转变换要注意旋转变换的三个要素:
1、旋转中心;
2、旋转的方向;
3、旋转的角度。
由一个图形变为另一个图形,在运动的过程中,原图形上的所有点都绕一个固定的点,按同一个方向,转动同一个角度,这样的图形运动叫做图形的旋转.这个固定的点叫做旋转中心。
什么是旋转
1、如图,经过怎样的旋转变换,可由射线OP得到射线OQ?
O
P
Q
答:将射线OP以O为旋转中心,按顺时针方向,
旋转90°得到射线OQ
说一说
2、本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
说一说
3.下列现象中属于旋转的有( )个
①地下水位逐年下降;②滑雪运动员在雪地上滑行;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
4、 如图, ABC是等边三角形,D是BC上一点, ABD
经过旋转后到达 ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过
旋转后,点M转到了什么位置?
E
D
C
B
A
M
.
解:(1)旋转中心是点A;
(2)旋转了60度;
(3)点M转到了AC的中点位置上.
解题心得:
(1)旋转的角度可由某一个特殊的旋转角得出;
(2)点的位置在旋转前后是相对应.
巩固概念与性质
若叶片 A 绕 O 顺时针旋转到叶片 B,则旋转中心是______,旋转角是_________,旋转角等于____度,其中的对应点有_______、 _______、 _______、 _______、 _______、 _______ 。
A
B
C
D
E
F
O
抢答
O
∠AOB
60
F与A
A与B
B与C
C与D
D与E
E与F
杠杆绕支点转动撬起重物,杠杆的旋转中心就____,旋转角是_______________________。
B
O
B′
A
A′
∠AOA′
O
∠BOB′
或
如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
1.旋转中心是什么?
2.经过旋转,点A,B, C
分别移动到什么位置?
3.AO与DO的长有什么关
系?BO与EO呢?
4.∠AOD与∠BOE有什
么大小关系? ∠COF呢?
说一说
(1)旋转不改变图形的形状和大小.
旋转变换的性质
(2)对应点到旋转中心的距离相等,对应点与
旋转中心的连线所成的角度等于旋转的角度.
1、如图,以点O为旋转中心,将点A按逆时针方向
旋转60°,作出经旋转变换后所得的图形。
2、如图,以点O为旋转中心,将线段AB按逆时针
方向旋转60°,作出经旋转变换后所得的图形
O
A
A
B
O
旋转变换的画图
例1、如图,O是△ABC外一点,以点O为旋转中心,
将△ABC按顺时针方向旋转60°,作出经旋转
变换后的像。
.
O
A
B
C
旋转变换的画图
如图,△ ABC绕点C旋转后,顶点A的对应点为点D。试确定顶点B对应点的位置,以及旋转后的三角形。
△DEC就是△ABC绕C点旋转变换后的像.
A
B
D
C
·
E
旋转变换的画图
1:如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
分析:关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
2.如图3-2-1所示,∠AOB=90°,∠B=30°,△A′OB′可以看作是由△AOB绕点O逆时针旋转α角度得到的.若点A′在AB上,则旋转角α的大小可以是
( )
图3-2-1
C
A.30° B.45°
C.60° D.90°
3.如图3-2-2所示,两个全等的正方形ABCD与CDEF,旋转正方形ABCD能和正方形CDEF重合,则可以作为旋转中心的点有______个.
图3-2-2
3
类型之一 旋转及其性质
例3 如图3-2-4所示,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
图3-2-4
(1)线段OA1的长是______.∠AOB1的度数是________;
(2)连结AA1,求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
6
135°
1.如图3-2-10,已知D为等边△ABC内一点,将△DBC绕点C旋转到△EAC的位置.试判断△CDE的形状,并证明你的结论.
图3-2-10
2.如图3-2-6,Rt△ABC是等腰三角形,D是Rt△ABC内一点,BC是斜边,如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置,则∠ADD′的度数是
( )
图3-2-6
D
A.25° B.30°
C.35° D.45°
3.如图3-2-11,把正方形ABCD绕点A按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.求证:HG=HB.
图3-2-11
1、相同:都是一种运动;运动前 后不改变图形的形状和大小
2、不同
形状 大小 方向
轴对称 不变 不变 改变
平移 不变 不变 不变
旋转 不变 不变 改变
3
方法一、先将牌A右下角顶点为旋转中心,将牌A按顺时针方向旋转90°,再向下作一次平移变换,就得到牌B.
方法二、先将牌A向下作一次平移变换,平移到牌A的右下角与牌B的左下角重合,再以牌A的右下角顶点为旋转中心,按顺时针方向旋转90°,再就得到牌B.
同课章节目录
