浙教版八年级上册 4.2 平面直角坐标系 课件(共19张PPT)
文档属性
| 名称 | 浙教版八年级上册 4.2 平面直角坐标系 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-02 00:00:00 | ||
图片预览

文档简介
(共19张PPT)
瓢城东望水漫漫,行到下菰城畔望
2022.5.31
4.2 平面直角坐标系
情境引入,一生二
A:江
K:苏
E:成
I:南
B:晶
H:才
G:正
C:德
L:浔
F:水
D:盐
J:修
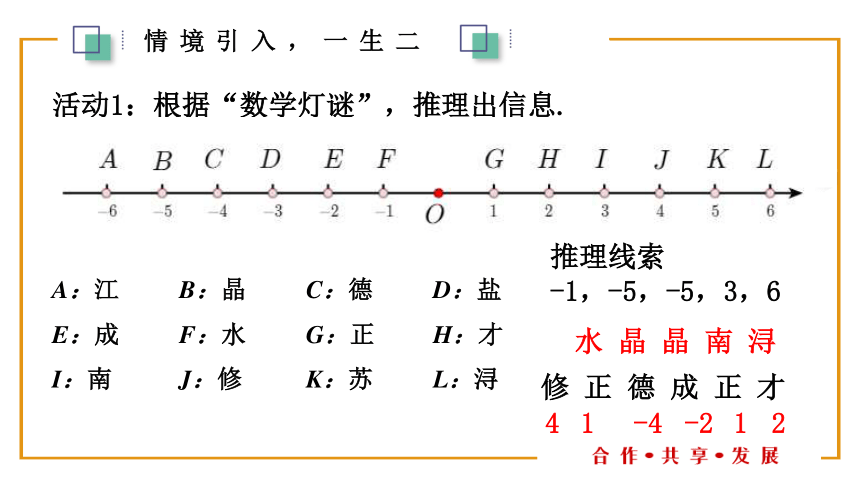
活动1:根据“数学灯谜”,推理出信息.
推理线索
-1,-5,-5,3,6
水 晶 晶 南 浔
修 正 德 成 正 才
4
1
-4
-2
1
2
情境引入,一生二
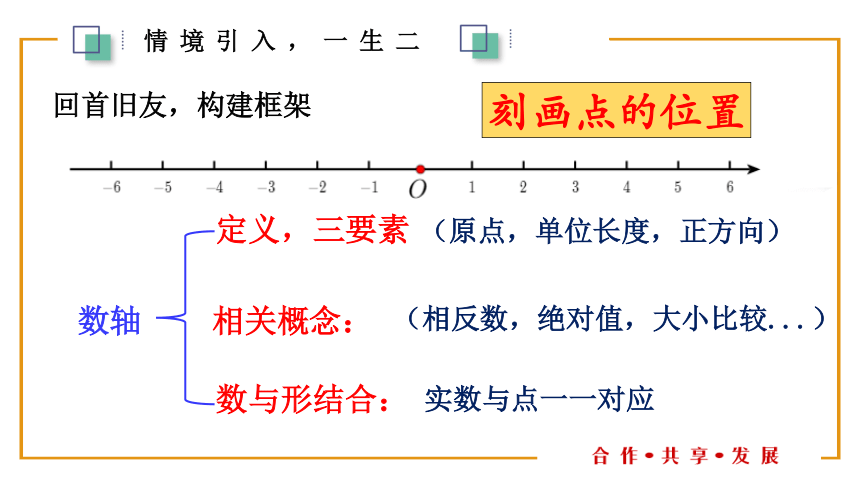
回首旧友,构建框架
数轴
定义,三要素
(原点,单位长度,正方向)
相关概念:
(相反数,绝对值,大小比较...)
数与形结合:
实数与点一一对应
刻画点的位置
情境升华,二生三
情境升华,二生三
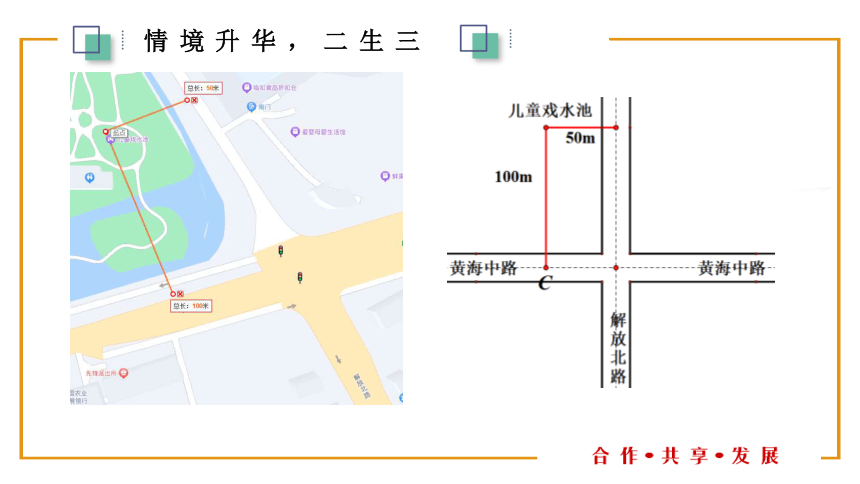
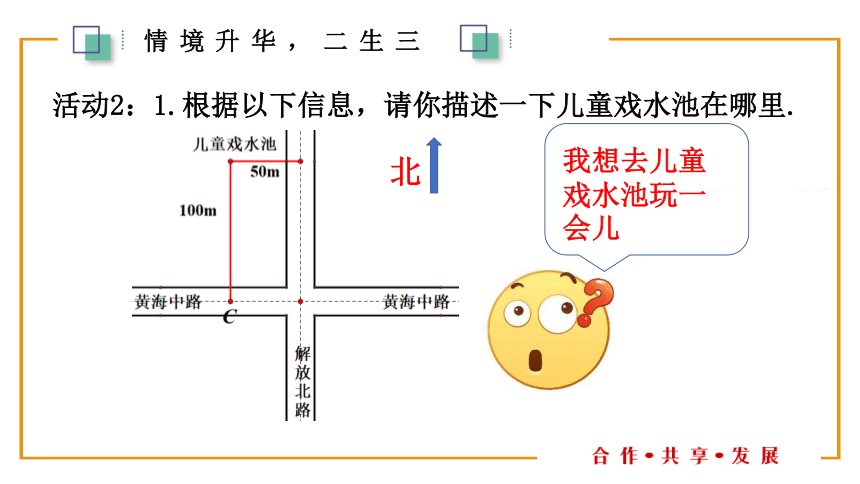
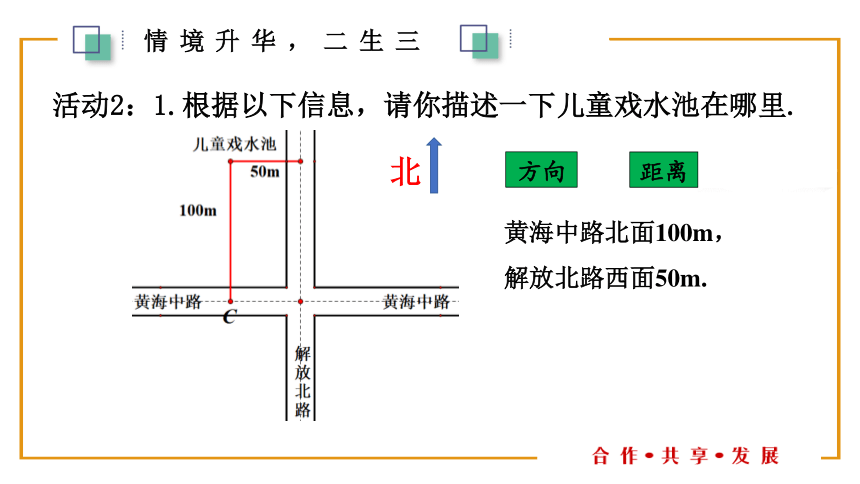
活动2:1.根据以下信息,请你描述一下儿童戏水池在哪里.
北
我想去儿童戏水池玩一会儿
情境升华,二生三
活动2:1.根据以下信息,请你描述一下儿童戏水池在哪里.
北
黄海中路北面100m,
解放北路西面50m.
方向
距离
情境升华,二生三
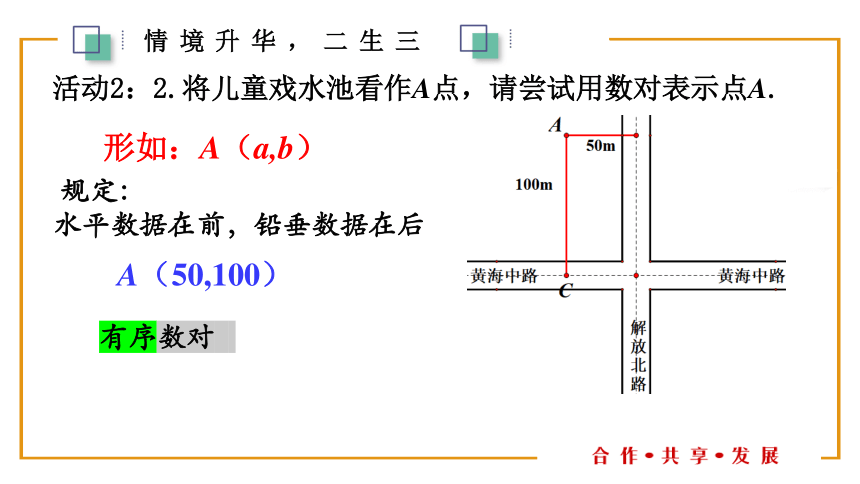
活动2:2.将儿童戏水池看作A点,请尝试用数对表示点A.
形如:A(a,b)
A(50,100)
规定:
水平数据在前,铅垂数据在后
有序数对
情境升华,二生三
活动2:3.若将盐城市田家炳中学看作点B,请你表达点B.
A(50,100)
有序数对
B(50,100)
A(-50,100)
情境升华,二生三
定义:平面内两条互相垂直的数轴构成平面直角坐标系,简称直角坐标系.
水平数轴:横轴—x轴
铅垂数轴:纵轴—y轴
正方向,原点
横轴
纵轴
公共原点
平面直角坐标系
横轴、纵轴统称为坐标轴
情境升华,二生三
活动3:1.如图在平面直角坐标系有点A和点B,
请将点A和点B用有序数对表示.
小结:任意一点的位置都可以用有序数对表示.即:点的位置→有序数对
①请你试一试,平面直角坐标系中的点C,D,E,F如何表示;
A(-2,4)
B(2,4)
②平面中的任意一点P如何用有序数对表示.
情境升华,二生三
金语点睛
点的位置
有序数对
点P
(a,b)
平面直角坐标系
形
数
直角坐标系中,点P的坐标,其中a是点P的横坐标,b是点P的纵坐标.
说说点的坐标
情境升华,二生三
活动3:2在该直角坐标系内,已知G,H,M,N对应的坐标(3,2),(-3,-3),(0,2),(-4,2)请你在坐标系内找到四点的位置;
小结:坐标可以确定点的位置.
②有坐标(a,b),能否确定对应点P的位置.
点P
(a,b)
情境升华,二生三
笛卡尔(1596-1660)
笛卡尔和直角坐标系
做中所悟,三生万物
活动4:小组活动
若需将现有10个点根据位置和坐标进行分类,小组交流分类方式并分享你们分类的依据,小组确定汇报人进行汇报交流.
做中所悟,三生万物
第一象限
第二象限
第三象限
第四象限
两条坐标轴将平面分成的4个区域称为象限,按逆时针顺序分别记为第一、二、三、四象限.
坐标轴不属于任何象限.
象限
做中所悟,三生万物
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴上
y轴上
+
+
-
-
+
-
+
-
a
0
0
b
探索内容
定义
横轴
纵轴
象限
探索模型
知识生长
探索方法
类比数轴
数形结合
...
感悟提升,回归本源
特殊到一般
做中所悟,三生万物
1.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
终章活动,做中所固
做中所悟,三生万物
2.在平面直角坐标系中,点P的坐标是(a,b),若ab>0,则点P在第________象限;若ab<0,则点P在第________象限;若ab=0,则点P在_________.
终章活动,做中所固
瓢城东望水漫漫,行到下菰城畔望
2022.5.31
4.2 平面直角坐标系
情境引入,一生二
A:江
K:苏
E:成
I:南
B:晶
H:才
G:正
C:德
L:浔
F:水
D:盐
J:修
活动1:根据“数学灯谜”,推理出信息.
推理线索
-1,-5,-5,3,6
水 晶 晶 南 浔
修 正 德 成 正 才
4
1
-4
-2
1
2
情境引入,一生二
回首旧友,构建框架
数轴
定义,三要素
(原点,单位长度,正方向)
相关概念:
(相反数,绝对值,大小比较...)
数与形结合:
实数与点一一对应
刻画点的位置
情境升华,二生三
情境升华,二生三
活动2:1.根据以下信息,请你描述一下儿童戏水池在哪里.
北
我想去儿童戏水池玩一会儿
情境升华,二生三
活动2:1.根据以下信息,请你描述一下儿童戏水池在哪里.
北
黄海中路北面100m,
解放北路西面50m.
方向
距离
情境升华,二生三
活动2:2.将儿童戏水池看作A点,请尝试用数对表示点A.
形如:A(a,b)
A(50,100)
规定:
水平数据在前,铅垂数据在后
有序数对
情境升华,二生三
活动2:3.若将盐城市田家炳中学看作点B,请你表达点B.
A(50,100)
有序数对
B(50,100)
A(-50,100)
情境升华,二生三
定义:平面内两条互相垂直的数轴构成平面直角坐标系,简称直角坐标系.
水平数轴:横轴—x轴
铅垂数轴:纵轴—y轴
正方向,原点
横轴
纵轴
公共原点
平面直角坐标系
横轴、纵轴统称为坐标轴
情境升华,二生三
活动3:1.如图在平面直角坐标系有点A和点B,
请将点A和点B用有序数对表示.
小结:任意一点的位置都可以用有序数对表示.即:点的位置→有序数对
①请你试一试,平面直角坐标系中的点C,D,E,F如何表示;
A(-2,4)
B(2,4)
②平面中的任意一点P如何用有序数对表示.
情境升华,二生三
金语点睛
点的位置
有序数对
点P
(a,b)
平面直角坐标系
形
数
直角坐标系中,点P的坐标,其中a是点P的横坐标,b是点P的纵坐标.
说说点的坐标
情境升华,二生三
活动3:2在该直角坐标系内,已知G,H,M,N对应的坐标(3,2),(-3,-3),(0,2),(-4,2)请你在坐标系内找到四点的位置;
小结:坐标可以确定点的位置.
②有坐标(a,b),能否确定对应点P的位置.
点P
(a,b)
情境升华,二生三
笛卡尔(1596-1660)
笛卡尔和直角坐标系
做中所悟,三生万物
活动4:小组活动
若需将现有10个点根据位置和坐标进行分类,小组交流分类方式并分享你们分类的依据,小组确定汇报人进行汇报交流.
做中所悟,三生万物
第一象限
第二象限
第三象限
第四象限
两条坐标轴将平面分成的4个区域称为象限,按逆时针顺序分别记为第一、二、三、四象限.
坐标轴不属于任何象限.
象限
做中所悟,三生万物
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
点的位置 横坐标符号 纵坐标符号
第一象限
第二象限
第三象限
第四象限
x轴上
y轴上
+
+
-
-
+
-
+
-
a
0
0
b
探索内容
定义
横轴
纵轴
象限
探索模型
知识生长
探索方法
类比数轴
数形结合
...
感悟提升,回归本源
特殊到一般
做中所悟,三生万物
1.下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
终章活动,做中所固
做中所悟,三生万物
2.在平面直角坐标系中,点P的坐标是(a,b),若ab>0,则点P在第________象限;若ab<0,则点P在第________象限;若ab=0,则点P在_________.
终章活动,做中所固
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
