浙教版八年级上册 4.2.1 平面直角坐标系课件(共18张PPT)
文档属性
| 名称 | 浙教版八年级上册 4.2.1 平面直角坐标系课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-02 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
4.2.1平面直角坐标系
预学反馈
1.请你站在班级讲台上,规定列号在前,排数在后,表示自己在班级的位置.
平面直角坐标系
P
P’
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
0
3
1
4
2
5
-2
-4
-1
-3
0
Q’
Q
利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
平面直角坐标系
在平面内画两条互相垂直,并且有公共原点O的数轴,其中一条叫做x轴(又叫横轴),通常画成水平,另一条叫做y轴(又叫纵轴),画成与x轴垂直.这样,我们就在平面内建立了平面直角坐标系,简称直角坐标系.两坐标轴的公共原点O叫做该直角坐标系的原点,这个平面叫坐标平面.
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
对于平面内任意一点 M,做MM1⊥x 轴, MM2⊥y 轴,设垂足为
M1,M2在各自数轴上所表示的数分别为x,y,则x叫做点 M 的横坐标,y叫做点M的纵坐标,有序实数对(x,y ) 叫做点 M 的坐标.
对于坐标平面内的任意一点,都可以找到一个有序实数对(x,y) 和它对应。
3
1
4
2
5
-2
-4
-1
-3
O
y
1
2
3
4
5
-4
-3
-2
-1
x
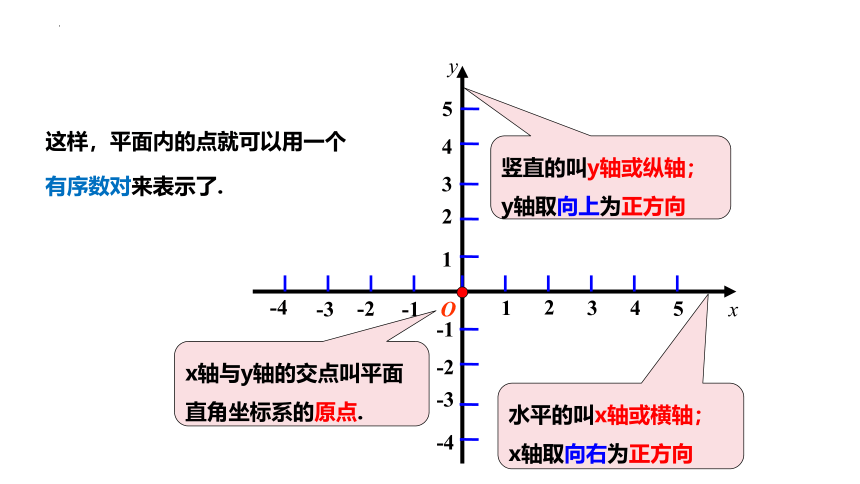
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
这样,平面内的点就可以用一个有序数对来表示了.
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
横坐标
纵坐标
请写出点B,C,D的坐标
( , )
0
2
( , )
0
-3
如图,由点A分别向 x轴和 y轴作垂线,垂足M在 x轴上的坐标是3,垂足 N在 y轴上的坐标是4.
M
N
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个部分.每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限.
注意:坐标轴上的点不属于任何一个象限.
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
建立了平面直角坐标系后,对于坐标平面内任何一点,我们可以确定它的坐标.反过来,对于任何一个坐标,我们可以在坐标平面内确定它所表示的一个点.
问题1: 观察如图坐标系, 填写各象限内的点的坐标的特征.
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
直角坐标系中坐标的特征
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
问题2: 观察如图坐标系, 填写坐标轴上的点的坐标的特征.
例1(1)如图,写出平面直角坐标系内点M,N,L,O,P的坐标.
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
·
N
·
M
·
P
L
(-2,2)
(2,4)
(2,-2.5)
(0,-2.5)
·
(0,0)
例1(2)在平面直角坐标系内画出点
A(2,4),
B(5,2),
C(-3.5,0),
D(-3.5,-2).
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
·
·
·
·
·
C
D
A
B
( +,+)
( -,+)
( - , - )
( +,-)
( 2,4 )
( -3.5,0)
( -3.5,-2)
( 5,2 )
笛卡尔(1596--1650)
法国伟大的数学家、哲学家、物理学家.
最早引入坐标系,用代数方法研究几何图形,是解析几何的创始人.
法国数学家笛卡儿设想将几何问题数量化,从而使其变成一个代数问题,用代数学的方法进行计算、证明,从而达到最终解决几何问题的目的,由此诞生了一门新的数学分支——解析几何。这好像在被一条大河隔开的代数和几何的两岸,架起了一座桥梁,把“数”与“形”联系起来,引起了数学的深刻革命。解析几何的诞生是数学发展的一个转折点。笛卡儿的这种思想,尤其在高速计算机出现的今天,具有深远意义。
精讲释疑
2.观察上题图中点的坐标特点,回答下列问题:
(1)x轴上的点的_________坐标是0
(2)y轴上的点的_________坐标是0
(3)点M到x轴的距离是_________,点M到y轴的距离是_________.
(4)点P到x轴的距离是_________,点P到y轴的距离是_________.
(5)点M在第_______象限,点N在第_______象限,点D在第_______象限,点P在第_______象限.
(6)点C在_______轴上,点L在_______轴上,坐标轴上的点_______(填“属于”“不属于”)任何象限.
巩固练习
1.如图,以图书馆为坐标原点建立平面直角坐标系,则西城广场的坐标为( )
A.(2,3) B.(0,3) C.(3,2) D.(2,2)
2.在平面直角坐标系xOy中,点M(-4,3)到x轴的距离是( )
A.-4 B.4 C.5 D.3
巩固练习
3.在平面直角坐标系中,已知点P(-2,3),则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4. 已知点A(4,2),B(-2,2),则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.以上都有可能
5.从学校出发,沿正南方向走150 m,再沿正东方向走200 m可到达小敏家,如果以学校的位置为原点,以正北、正东方向为y轴、x轴的正方向,1 m表示一个单位长度建立平面直角坐标系,那么小敏家的位置用坐标表示为 .
课堂小结
平面直角坐标系
在平面内画两条互相垂直的数轴, 构成平面直角坐标系.
第一象限: (+, +), 第二象限: (-, +),
第三象限: (-, -), 第四象限: (+, -).
x轴上的点的纵坐标为0, 表示为(x, 0).
y轴上的点的横坐标为0, 表示为(0, y).
坐标平面内的点与有序实数对是一一对应的.
感谢观看!
4.2.1平面直角坐标系
预学反馈
1.请你站在班级讲台上,规定列号在前,排数在后,表示自己在班级的位置.
平面直角坐标系
P
P’
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
0
3
1
4
2
5
-2
-4
-1
-3
0
Q’
Q
利用数轴确定直线上的点的位置,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系.
平面直角坐标系
在平面内画两条互相垂直,并且有公共原点O的数轴,其中一条叫做x轴(又叫横轴),通常画成水平,另一条叫做y轴(又叫纵轴),画成与x轴垂直.这样,我们就在平面内建立了平面直角坐标系,简称直角坐标系.两坐标轴的公共原点O叫做该直角坐标系的原点,这个平面叫坐标平面.
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
对于平面内任意一点 M,做MM1⊥x 轴, MM2⊥y 轴,设垂足为
M1,M2在各自数轴上所表示的数分别为x,y,则x叫做点 M 的横坐标,y叫做点M的纵坐标,有序实数对(x,y ) 叫做点 M 的坐标.
对于坐标平面内的任意一点,都可以找到一个有序实数对(x,y) 和它对应。
3
1
4
2
5
-2
-4
-1
-3
O
y
1
2
3
4
5
-4
-3
-2
-1
x
竖直的叫y轴或纵轴;
y轴取向上为正方向
水平的叫x轴或横轴;
x轴取向右为正方向
x轴与y轴的交点叫平面直角坐标系的原点.
这样,平面内的点就可以用一个有序数对来表示了.
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
( , )
3
4
( , )
-3
-4
横坐标
纵坐标
请写出点B,C,D的坐标
( , )
0
2
( , )
0
-3
如图,由点A分别向 x轴和 y轴作垂线,垂足M在 x轴上的坐标是3,垂足 N在 y轴上的坐标是4.
M
N
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个部分.每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限.
注意:坐标轴上的点不属于任何一个象限.
Ⅳ
Ⅰ
Ⅱ
Ⅲ
x
y
O
1 2 3 4
5
4
3
2
1
-4 -3 -2 -1
-1
-2
-3
-4
第一象限
第二象限
第四象限
第三象限
建立了平面直角坐标系后,对于坐标平面内任何一点,我们可以确定它的坐标.反过来,对于任何一个坐标,我们可以在坐标平面内确定它所表示的一个点.
问题1: 观察如图坐标系, 填写各象限内的点的坐标的特征.
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
直角坐标系中坐标的特征
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
问题2: 观察如图坐标系, 填写坐标轴上的点的坐标的特征.
例1(1)如图,写出平面直角坐标系内点M,N,L,O,P的坐标.
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
·
N
·
M
·
P
L
(-2,2)
(2,4)
(2,-2.5)
(0,-2.5)
·
(0,0)
例1(2)在平面直角坐标系内画出点
A(2,4),
B(5,2),
C(-3.5,0),
D(-3.5,-2).
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
x
·
·
·
·
·
C
D
A
B
( +,+)
( -,+)
( - , - )
( +,-)
( 2,4 )
( -3.5,0)
( -3.5,-2)
( 5,2 )
笛卡尔(1596--1650)
法国伟大的数学家、哲学家、物理学家.
最早引入坐标系,用代数方法研究几何图形,是解析几何的创始人.
法国数学家笛卡儿设想将几何问题数量化,从而使其变成一个代数问题,用代数学的方法进行计算、证明,从而达到最终解决几何问题的目的,由此诞生了一门新的数学分支——解析几何。这好像在被一条大河隔开的代数和几何的两岸,架起了一座桥梁,把“数”与“形”联系起来,引起了数学的深刻革命。解析几何的诞生是数学发展的一个转折点。笛卡儿的这种思想,尤其在高速计算机出现的今天,具有深远意义。
精讲释疑
2.观察上题图中点的坐标特点,回答下列问题:
(1)x轴上的点的_________坐标是0
(2)y轴上的点的_________坐标是0
(3)点M到x轴的距离是_________,点M到y轴的距离是_________.
(4)点P到x轴的距离是_________,点P到y轴的距离是_________.
(5)点M在第_______象限,点N在第_______象限,点D在第_______象限,点P在第_______象限.
(6)点C在_______轴上,点L在_______轴上,坐标轴上的点_______(填“属于”“不属于”)任何象限.
巩固练习
1.如图,以图书馆为坐标原点建立平面直角坐标系,则西城广场的坐标为( )
A.(2,3) B.(0,3) C.(3,2) D.(2,2)
2.在平面直角坐标系xOy中,点M(-4,3)到x轴的距离是( )
A.-4 B.4 C.5 D.3
巩固练习
3.在平面直角坐标系中,已知点P(-2,3),则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4. 已知点A(4,2),B(-2,2),则直线AB( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.以上都有可能
5.从学校出发,沿正南方向走150 m,再沿正东方向走200 m可到达小敏家,如果以学校的位置为原点,以正北、正东方向为y轴、x轴的正方向,1 m表示一个单位长度建立平面直角坐标系,那么小敏家的位置用坐标表示为 .
课堂小结
平面直角坐标系
在平面内画两条互相垂直的数轴, 构成平面直角坐标系.
第一象限: (+, +), 第二象限: (-, +),
第三象限: (-, -), 第四象限: (+, -).
x轴上的点的纵坐标为0, 表示为(x, 0).
y轴上的点的横坐标为0, 表示为(0, y).
坐标平面内的点与有序实数对是一一对应的.
感谢观看!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
