浙教版八年级下册 1.3 二次根式的运算 课件(共26张PPT)
文档属性
| 名称 | 浙教版八年级下册 1.3 二次根式的运算 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 00:00:00 | ||
图片预览



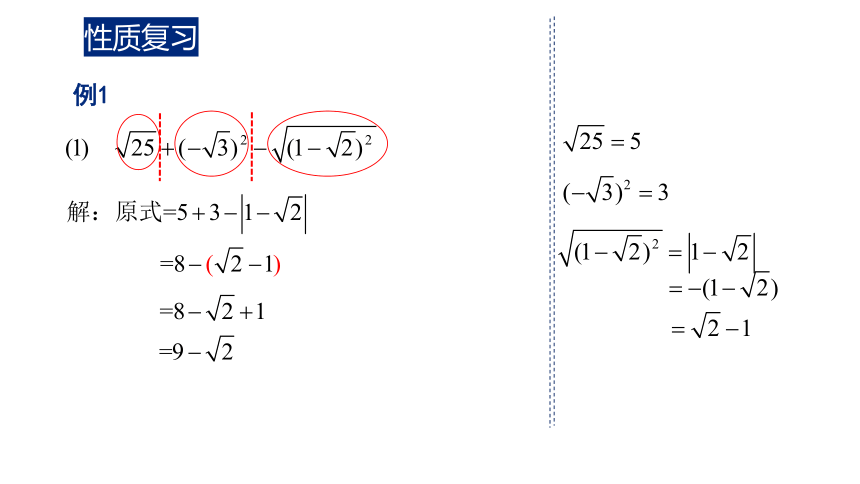

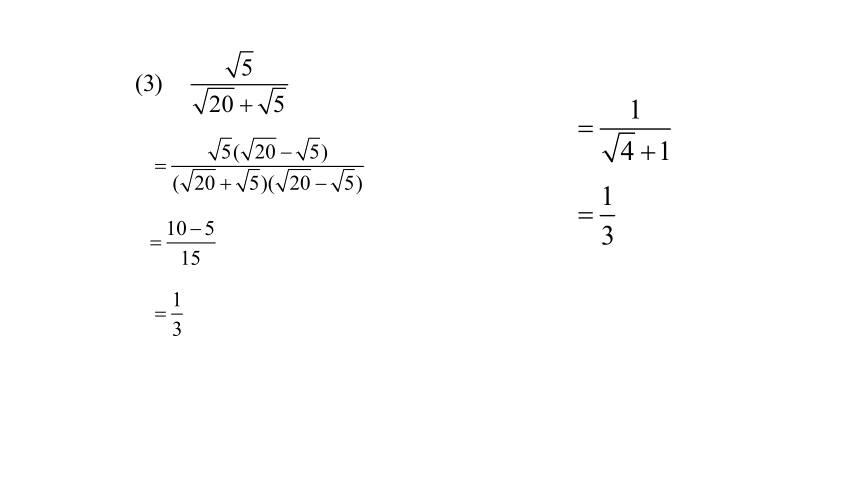
文档简介
(共26张PPT)
——八年级下册第一章《1.3二次根式的运算(3)》
概念回顾
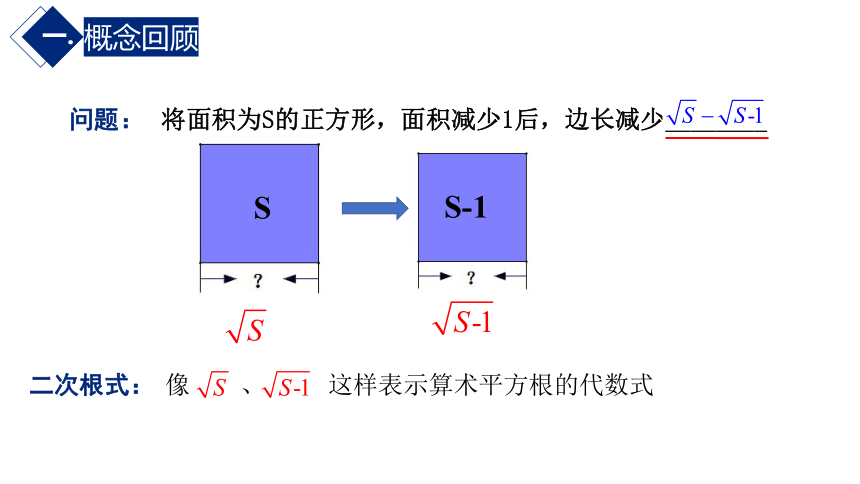
问题:
S
S-1
二次根式:
像 、 这样表示算术平方根的代数式
将面积为S的正方形,面积减少1后,边长减少________
一.
变式练习
二.
变式1 化简
二次根式的性质
性质复习
三.
计算:
例1
性质复习
三.
例1
性质复习
三.
例1 计算
1.根号内是一个不含平方因数的整数
最简二次根式
化成最简二次根式
2.分母中不含根号
引入新知
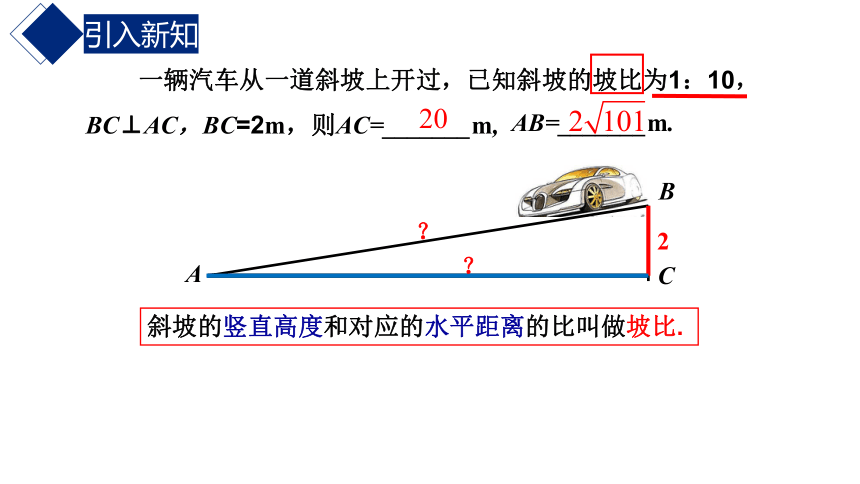
一辆汽车从一道斜坡上开过,已知斜坡的坡比为1:10,BC⊥AC,BC=2m,则AC=_______m,
斜坡的竖直高度和对应的水平距离的比叫做坡比.
A
B
C
AB=_______m.
20
2
?
?
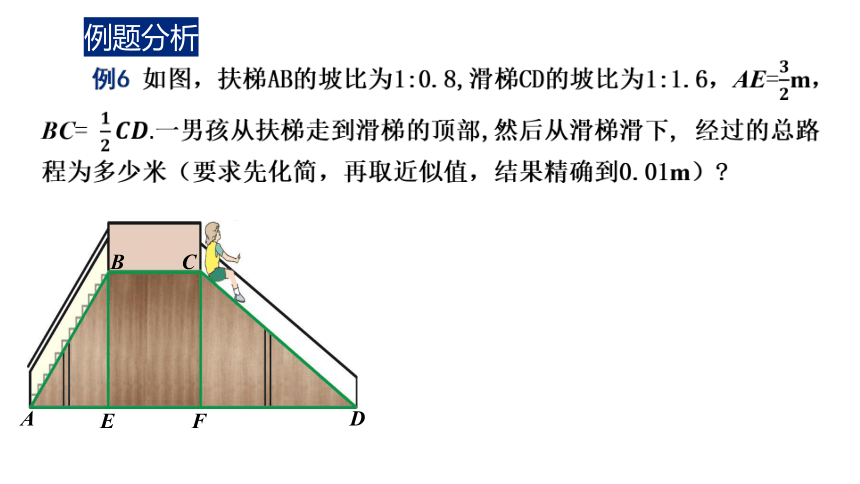
例题分析
例6 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,AE=m,BC= 一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下, 经过的总路程为多少米(要求先化简,再取近似值,结果精确到0.01m)
A
B
C
D
E
F
例题分析
例6 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,AE=m,BC= 一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下, 经过的总路程为多少米(要求先化简,再取近似值,结果精确到0.01m)
A
B
C
D
E
F
解:
∴BC
=
∵CD= m
= m
∴AB+BC+CD= + +
= +
≈7.71(m)
答:这个小男孩经过的总路程约为7.71米.
在RtAEB中,
∵AE=(m),
(m)
∴BE=AE÷0.8= (m)
=
=
在Rt CFD中,
∵CF= BE=,
∴DF=1.6CF (m)
∴CD
∴AB
=
= (m)
例题分析
例6 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,AE=m,BC= 一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下, 经过的总路程为多少米(要求先化简,再取近似值,结果精确到0.01m)
A
B
C
D
E
F
解:
∴BC
=
∵CD= m
= m
∴AB+BC+CD= + +
= +
≈7.71(m)
答:这个小男孩经过的总路程约为7.71米.
在RtAEB中,
∵AE=(m),
(m)
∴BE=AE÷0.8= (m)
=
=
在Rt CFD中,
∵CF= BE=,
∴DF=1.6CF (m)
∴CD
∴AB
=
= (m)
方法总结:
例题分析
1.审题:找出已知量和未知量;
2.列式:建立已知量和未知量关系;
3.计算:二次根式的性质及运算法则.
例题分析
例7引例
如图1是一张等腰直角三角形彩色纸,AC=BC=40cm,CD是斜边上的高.
(1)求AB和CD的长;
C
D
A
B
图1
例题分析
如图1是一张等腰直角三角形彩色纸,AC=BC=40cm,CD是斜边上的高.
(1)求AB和CD的长;
(1)∵∠ACB=90°, AC=BC=40cm
解:
∵CD⊥AB,AC=BC
∴ AD=BD
C
D
A
B
图1
例7引例
例题分析
例7引例
如图1,是一张等腰直角三角形彩色纸,AC=BC=40cm,CD是斜边上的高.
C
D
A
B
图2
(2)如图2,小明将斜边上的高CD二等分,然后裁出1张长方形纸条.请求出这张长方形纸条的长和宽.
(1)AB= 40cm ,CD= 20cm.
E
F
G
认真审题,完成题目,限时2分钟!
例题分析
例7引例
如图1,是一张等腰直角三角形彩色纸,AC=BC=40cm,CD是斜边上的高.
C
D
A
B
图2
(2)如图2,小明将斜边上的高CD二等分,然后裁出1张长方形纸条.请求出这张长方形纸条的长和宽.
(1)AB= 40cm ;CD= 20cm.
E
F
G
例题分析
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
C
D
A
B
F
E
H
G
J
I
M
N
P
(1)分别求出三张长方形纸条的长度.
例题分析
C
D
A
B
F
E
H
G
J
I
M
N
P
解:
∵AC=BC, ∠ACB=90°
∴∠A =45°
同理可得,
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
(1)分别求出三张长方形纸条的长度.
∵CM⊥EF
∴∠CEF =∠A =45°
∵EF∥AB, ∠A =45
例题分析
C
D
A
B
F
E
H
G
J
I
M
N
P
解:
∵CD= 20cm
∴CM= = 5cm
∵AC=BC, ∠ACB=90°
∴∠A =45°
∴EF=2CM=10cm
同理可得,
GH=2 N
=2 × 10
= 20
IJ=2 = 30
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
(1)分别求出三张长方形纸条的长度.
∵CM⊥EF
∴∠CEF =∠A =45°
∵EF∥AB, ∠A =45
隐含条件
例题分析
A
B
C
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出三张宽度相等的长方形纸条.
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠), 正方形美术作品的面积为多少平方厘米?
例题分析
解:
(2)三张长方形连接在一起的总长度为:
答:正方形美术作品的面积为200平方厘米.
A
B
C
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出三张宽度相等的长方形纸条.
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠), 正方形美术作品的面积为多少平方厘米?
?
拓展提升
如图,一张边长为22cm的等边三角形彩色纸,小明在等边三角形纸片中裁出三条宽度相同的长方形纸条,其中最上面的那个长方形恰好为正方形,分别求出三张长方形纸条的长度.
拓展提升
拓展提升
如图,一张边长为22cm的等边三角形彩色纸,CD⊥AB,小明在等边三角形纸片中裁出三条宽度相同的长方形纸条,其中最上面的那个长方形恰好为正方形,分别求出三张长方形纸条的长度.
拓展提升
22
22
22
解:
?
巩固练习
在Rt△ABC中,∠C=Rt∠,AB=c,BC=a,AC=b.
(1)若,则
(2)若,则
A
B
C
巩固练习
在Rt△ABC中,∠C=Rt∠,AB=c,BC=a,AC=b.
(1)若,则
(2)若,则
A
B
C
方法总结:
二次根式的运算
直角三角形三边计算
感悟提升
一个概念
三个步骤
斜坡的竖直高度和对应的水平宽度的比叫做坡比
1.审题:找出已知量和未知量
2.列式:建立已知量和未知量关系
3.计算:二次根式的性质及运算法则
隐含条件
作业布置
作业A:《1.3二次根式(2)》P3-4作业本1-6.
作业B:《1.3二次根式(2)》P9-10课时特训10-13.
——八年级下册第一章《1.3二次根式的运算(3)》
概念回顾
问题:
S
S-1
二次根式:
像 、 这样表示算术平方根的代数式
将面积为S的正方形,面积减少1后,边长减少________
一.
变式练习
二.
变式1 化简
二次根式的性质
性质复习
三.
计算:
例1
性质复习
三.
例1
性质复习
三.
例1 计算
1.根号内是一个不含平方因数的整数
最简二次根式
化成最简二次根式
2.分母中不含根号
引入新知
一辆汽车从一道斜坡上开过,已知斜坡的坡比为1:10,BC⊥AC,BC=2m,则AC=_______m,
斜坡的竖直高度和对应的水平距离的比叫做坡比.
A
B
C
AB=_______m.
20
2
?
?
例题分析
例6 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,AE=m,BC= 一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下, 经过的总路程为多少米(要求先化简,再取近似值,结果精确到0.01m)
A
B
C
D
E
F
例题分析
例6 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,AE=m,BC= 一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下, 经过的总路程为多少米(要求先化简,再取近似值,结果精确到0.01m)
A
B
C
D
E
F
解:
∴BC
=
∵CD= m
= m
∴AB+BC+CD= + +
= +
≈7.71(m)
答:这个小男孩经过的总路程约为7.71米.
在RtAEB中,
∵AE=(m),
(m)
∴BE=AE÷0.8= (m)
=
=
在Rt CFD中,
∵CF= BE=,
∴DF=1.6CF (m)
∴CD
∴AB
=
= (m)
例题分析
例6 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,AE=m,BC= 一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下, 经过的总路程为多少米(要求先化简,再取近似值,结果精确到0.01m)
A
B
C
D
E
F
解:
∴BC
=
∵CD= m
= m
∴AB+BC+CD= + +
= +
≈7.71(m)
答:这个小男孩经过的总路程约为7.71米.
在RtAEB中,
∵AE=(m),
(m)
∴BE=AE÷0.8= (m)
=
=
在Rt CFD中,
∵CF= BE=,
∴DF=1.6CF (m)
∴CD
∴AB
=
= (m)
方法总结:
例题分析
1.审题:找出已知量和未知量;
2.列式:建立已知量和未知量关系;
3.计算:二次根式的性质及运算法则.
例题分析
例7引例
如图1是一张等腰直角三角形彩色纸,AC=BC=40cm,CD是斜边上的高.
(1)求AB和CD的长;
C
D
A
B
图1
例题分析
如图1是一张等腰直角三角形彩色纸,AC=BC=40cm,CD是斜边上的高.
(1)求AB和CD的长;
(1)∵∠ACB=90°, AC=BC=40cm
解:
∵CD⊥AB,AC=BC
∴ AD=BD
C
D
A
B
图1
例7引例
例题分析
例7引例
如图1,是一张等腰直角三角形彩色纸,AC=BC=40cm,CD是斜边上的高.
C
D
A
B
图2
(2)如图2,小明将斜边上的高CD二等分,然后裁出1张长方形纸条.请求出这张长方形纸条的长和宽.
(1)AB= 40cm ,CD= 20cm.
E
F
G
认真审题,完成题目,限时2分钟!
例题分析
例7引例
如图1,是一张等腰直角三角形彩色纸,AC=BC=40cm,CD是斜边上的高.
C
D
A
B
图2
(2)如图2,小明将斜边上的高CD二等分,然后裁出1张长方形纸条.请求出这张长方形纸条的长和宽.
(1)AB= 40cm ;CD= 20cm.
E
F
G
例题分析
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
C
D
A
B
F
E
H
G
J
I
M
N
P
(1)分别求出三张长方形纸条的长度.
例题分析
C
D
A
B
F
E
H
G
J
I
M
N
P
解:
∵AC=BC, ∠ACB=90°
∴∠A =45°
同理可得,
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
(1)分别求出三张长方形纸条的长度.
∵CM⊥EF
∴∠CEF =∠A =45°
∵EF∥AB, ∠A =45
例题分析
C
D
A
B
F
E
H
G
J
I
M
N
P
解:
∵CD= 20cm
∴CM= = 5cm
∵AC=BC, ∠ACB=90°
∴∠A =45°
∴EF=2CM=10cm
同理可得,
GH=2 N
=2 × 10
= 20
IJ=2 = 30
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
(1)分别求出三张长方形纸条的长度.
∵CM⊥EF
∴∠CEF =∠A =45°
∵EF∥AB, ∠A =45
隐含条件
例题分析
A
B
C
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出三张宽度相等的长方形纸条.
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠), 正方形美术作品的面积为多少平方厘米?
例题分析
解:
(2)三张长方形连接在一起的总长度为:
答:正方形美术作品的面积为200平方厘米.
A
B
C
例7 如图,一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出三张宽度相等的长方形纸条.
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠), 正方形美术作品的面积为多少平方厘米?
?
拓展提升
如图,一张边长为22cm的等边三角形彩色纸,小明在等边三角形纸片中裁出三条宽度相同的长方形纸条,其中最上面的那个长方形恰好为正方形,分别求出三张长方形纸条的长度.
拓展提升
拓展提升
如图,一张边长为22cm的等边三角形彩色纸,CD⊥AB,小明在等边三角形纸片中裁出三条宽度相同的长方形纸条,其中最上面的那个长方形恰好为正方形,分别求出三张长方形纸条的长度.
拓展提升
22
22
22
解:
?
巩固练习
在Rt△ABC中,∠C=Rt∠,AB=c,BC=a,AC=b.
(1)若,则
(2)若,则
A
B
C
巩固练习
在Rt△ABC中,∠C=Rt∠,AB=c,BC=a,AC=b.
(1)若,则
(2)若,则
A
B
C
方法总结:
二次根式的运算
直角三角形三边计算
感悟提升
一个概念
三个步骤
斜坡的竖直高度和对应的水平宽度的比叫做坡比
1.审题:找出已知量和未知量
2.列式:建立已知量和未知量关系
3.计算:二次根式的性质及运算法则
隐含条件
作业布置
作业A:《1.3二次根式(2)》P3-4作业本1-6.
作业B:《1.3二次根式(2)》P9-10课时特训10-13.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
