浙教版八年级下册 4.1 多边形 课件(共15张PPT)
文档属性
| 名称 | 浙教版八年级下册 4.1 多边形 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 09:55:29 | ||
图片预览


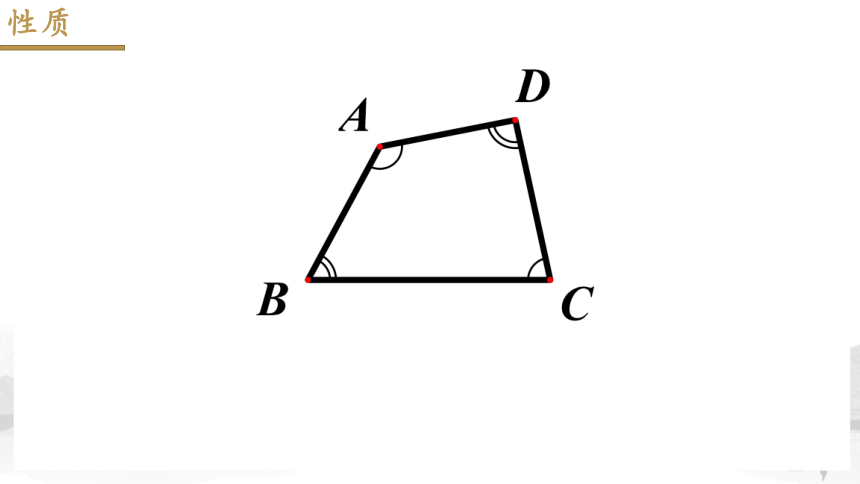

文档简介
(共15张PPT)
你能找到哪些几何图形?
浙教版义务教育教科书八下第四章第一节
多边形
回忆
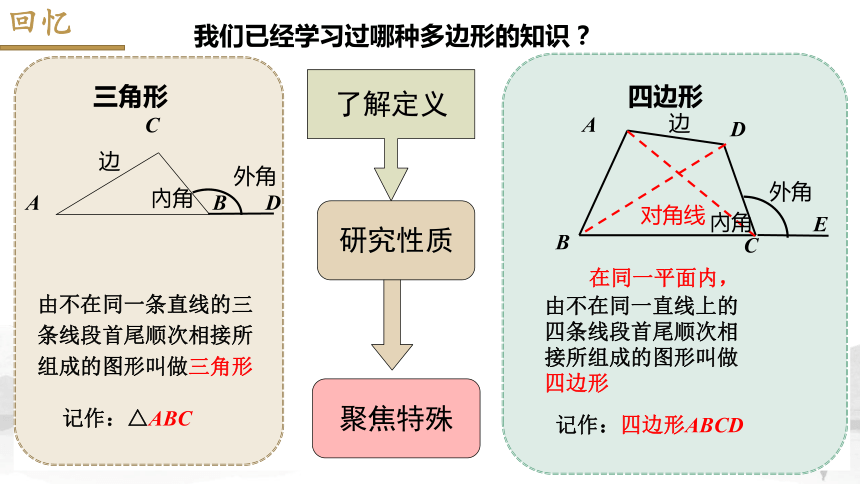
我们已经学习过哪种多边形的知识?
了解定义
研究性质
聚焦特殊
三角形
四边形
A
B
C
A
B
C
D
由不在同一条直线的三条线段首尾顺次相接所组成的图形叫做三角形
E
边
边
D
外角
外角
对角线
內角
內角
由不在同一直线上的四条线段首尾顺次相接所组成的图形叫做四边形
在同一平面内,
记作:四边形ABCD
记作:△ABC
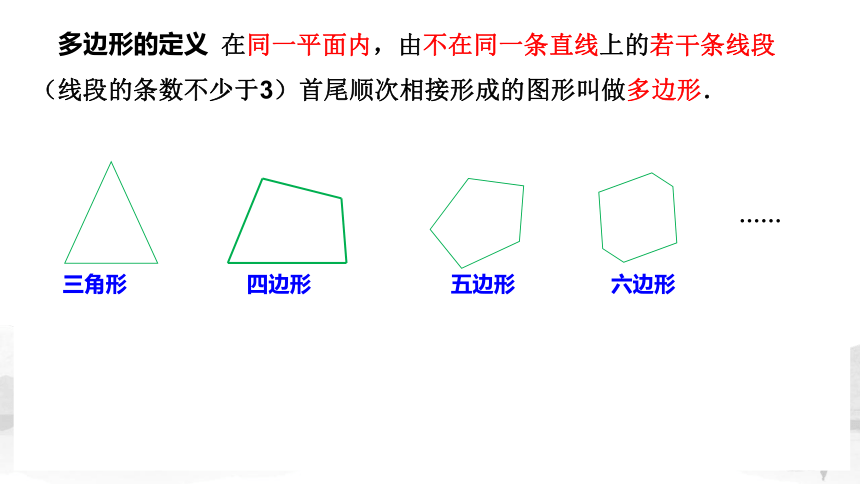
多边形的定义
在同一平面内,由不在同一条直线上的若干条线段(线段的条数不少于3)首尾顺次相接形成的图形叫做多边形.
……
三角形
四边形
五边形
六边形
回忆
了解定义
聚焦特殊
三角形
四边形
A
B
C
A
B
C
D
研究性质
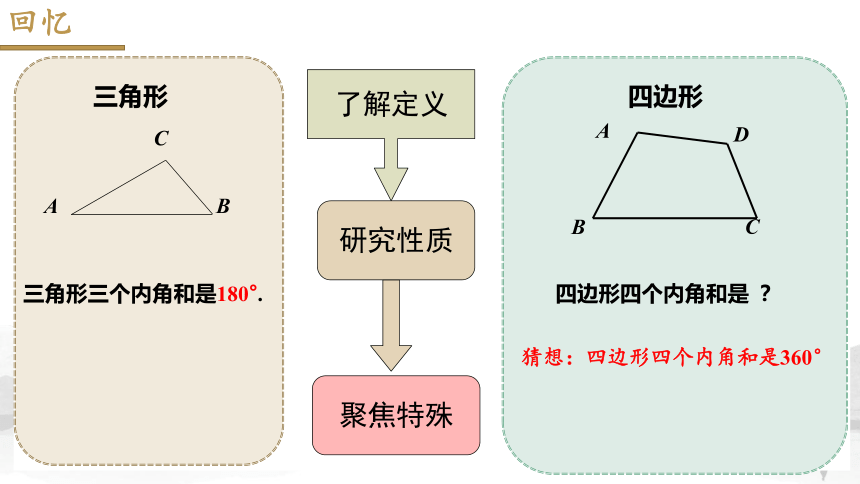
三角形三个内角和是180°.
四边形四个内角和是 ?
猜想:四边形四个内角和是360°
性质
性质
转化思想
已知:四边形ABCD(如图)
求证: ∠A +∠B + ∠C + ∠D=360°
探索:四边形的内角和等于多少度?
∵ ∠B+∠BAC+ ∠BCA =180 °
∠D+∠DCA+ ∠CAD =180 °
(三角形三个内角的和等于180 °)
即∠BAD+∠B+∠BCD+∠D=360 °
证明:连结AC
∴ ∠B+∠BAC+ ∠BCA+ ∠D+∠DCA+ ∠CAD =180 °+ 180° = 360°
性质
例 如图,四边形风筝的四个内角∠A、∠B、∠C、∠D的度数之比为1∶1∶0.6∶1。求它的四个内角的度数.
A
B
C
D
(四边形的内角和等于360 )
应用
1.已知四边形ABCD中, ∠A=80 °, ∠B=60°, ∠C=70°则∠D=_____.
2.如图,在四边形ABCD中,∠A=85°,∠D=110°, ∠1的外角是71°,则∠1=______,∠2=______。
150°
56°
109°
巩固
A
B
C
D
1
2
3
4
1+ 2+ 3+ 4=360°
四边形的外角有何性质?
∠1+∠BAD=180°
∠2+∠ABC=180°
∠1+∠2+∠3+∠4+∠BAD+∠ABC+∠BCD+∠CDA=180°×4
∠3+∠BCD=180°
∠4+∠CDA=180°
A
B
C
D
1
2
3
4
方法二:
用外角转化
∠2=∠BAC+∠BCA
∠4=∠DAC+∠DCA
探究
谈一谈,这节课我们学习了什么?
你有怎样的感悟与收获?
了解定义
聚焦特殊
研究性质
四边形内角和为360°
四边形外角和为360°
四种思想方法
类比思想 转化思想
方程思想 数形结合
四边形
A
B
C
D
边
外角
对角线
內角
由不在同一直线上的四条线段首尾顺次相接所组成的图形叫做四边形
在同一平面内,
记作:四边形ABCD
E
平行四边形
矩形
菱形
正方形
类比思想、转化思想、方程思想
三角形
正方形
长方形
任意四边形?
任意五边形?
拓展
2015年,三位数学家发现第15种不规则五
边形,可以在相互不重叠的情况下实现完
美无缝拼接。研究团队表示,这一发现无
异于发现一种新型粒子。
拓展
你能找到哪些几何图形?
浙教版义务教育教科书八下第四章第一节
多边形
回忆
我们已经学习过哪种多边形的知识?
了解定义
研究性质
聚焦特殊
三角形
四边形
A
B
C
A
B
C
D
由不在同一条直线的三条线段首尾顺次相接所组成的图形叫做三角形
E
边
边
D
外角
外角
对角线
內角
內角
由不在同一直线上的四条线段首尾顺次相接所组成的图形叫做四边形
在同一平面内,
记作:四边形ABCD
记作:△ABC
多边形的定义
在同一平面内,由不在同一条直线上的若干条线段(线段的条数不少于3)首尾顺次相接形成的图形叫做多边形.
……
三角形
四边形
五边形
六边形
回忆
了解定义
聚焦特殊
三角形
四边形
A
B
C
A
B
C
D
研究性质
三角形三个内角和是180°.
四边形四个内角和是 ?
猜想:四边形四个内角和是360°
性质
性质
转化思想
已知:四边形ABCD(如图)
求证: ∠A +∠B + ∠C + ∠D=360°
探索:四边形的内角和等于多少度?
∵ ∠B+∠BAC+ ∠BCA =180 °
∠D+∠DCA+ ∠CAD =180 °
(三角形三个内角的和等于180 °)
即∠BAD+∠B+∠BCD+∠D=360 °
证明:连结AC
∴ ∠B+∠BAC+ ∠BCA+ ∠D+∠DCA+ ∠CAD =180 °+ 180° = 360°
性质
例 如图,四边形风筝的四个内角∠A、∠B、∠C、∠D的度数之比为1∶1∶0.6∶1。求它的四个内角的度数.
A
B
C
D
(四边形的内角和等于360 )
应用
1.已知四边形ABCD中, ∠A=80 °, ∠B=60°, ∠C=70°则∠D=_____.
2.如图,在四边形ABCD中,∠A=85°,∠D=110°, ∠1的外角是71°,则∠1=______,∠2=______。
150°
56°
109°
巩固
A
B
C
D
1
2
3
4
1+ 2+ 3+ 4=360°
四边形的外角有何性质?
∠1+∠BAD=180°
∠2+∠ABC=180°
∠1+∠2+∠3+∠4+∠BAD+∠ABC+∠BCD+∠CDA=180°×4
∠3+∠BCD=180°
∠4+∠CDA=180°
A
B
C
D
1
2
3
4
方法二:
用外角转化
∠2=∠BAC+∠BCA
∠4=∠DAC+∠DCA
探究
谈一谈,这节课我们学习了什么?
你有怎样的感悟与收获?
了解定义
聚焦特殊
研究性质
四边形内角和为360°
四边形外角和为360°
四种思想方法
类比思想 转化思想
方程思想 数形结合
四边形
A
B
C
D
边
外角
对角线
內角
由不在同一直线上的四条线段首尾顺次相接所组成的图形叫做四边形
在同一平面内,
记作:四边形ABCD
E
平行四边形
矩形
菱形
正方形
类比思想、转化思想、方程思想
三角形
正方形
长方形
任意四边形?
任意五边形?
拓展
2015年,三位数学家发现第15种不规则五
边形,可以在相互不重叠的情况下实现完
美无缝拼接。研究团队表示,这一发现无
异于发现一种新型粒子。
拓展
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
