浙教版数学八年级下册 5.2.1 菱形 说课课件(共27张PPT)
文档属性
| 名称 | 浙教版数学八年级下册 5.2.1 菱形 说课课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 12:34:53 | ||
图片预览








文档简介
(共27张PPT)
5.2.1 菱形
立意素养 基于测评
说课流程
01
内容及内容解析
02
目标及目标解析
03
教学问题诊断分析
05
教学过程设计
06
目标评价设计
04
教学技术支持条件
平行四边形
矩形
正方形
定义
性质
判定
应用
角特殊
边特殊
类比
01
内容及内容解析
本节课的教学重点:探索并证明菱形的性质
类比
菱形
02
目标及目标解析
对照课标要求
课标要求 课时目标 目标解析
1.理解菱形的概念,以及菱形与平行四边形之间的关系. 2.探索并证明菱形的性质定理:菱形的四条边相等,对角线互相垂直. 3.探索菱形的轴对称性. 1.理解菱形的概念,以及菱形与平行四边形的关系. 2.探索并证明菱形的性质定理:菱形的四条边相等. 3.探索并证明菱形的性质定理:对角线互相垂直,并每条对角线平分一组对角. 4.探索菱形的轴对称性. 1.学生能说出菱形与平行四边形的关系,概括出菱形的概念(文字语言和符号语言).
2.学生能说出菱形的四条边相等,并给出证明.
3. 猜想、验证、证明、归纳出菱形对角线互相垂直,并每条对角线平分一组对角.
4.学生通过折、剪、拼明确菱形是轴对称图形,并能说出它的对称轴.
目标确定
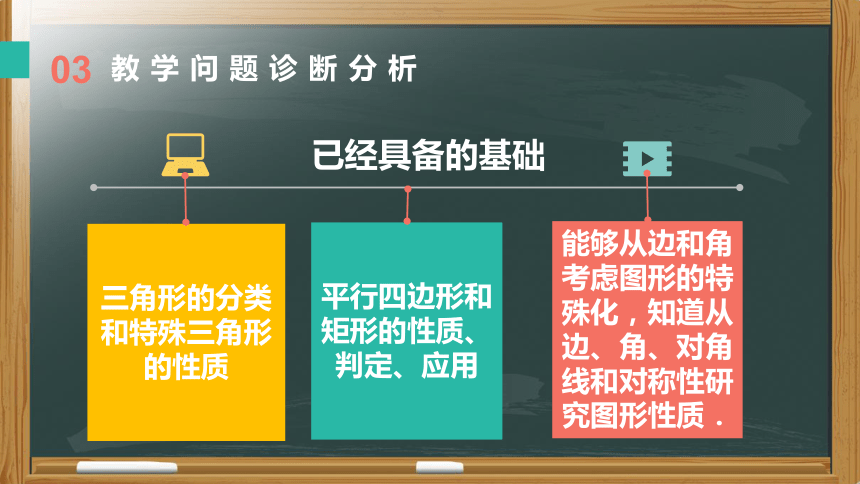
三角形的分类和特殊三角形的性质
平行四边形和矩形的性质、判定、应用
能够从边和角考虑图形的特殊化,知道从边、角、对角线和对称性研究图形性质.
已经具备的基础
03
教学问题诊断分析
可能存在的问题
课时目标 可能问题
1.理解菱形的概念,以及菱形与平行四边形的关系. 菱形与平行四边形的关系学生难以理解.
2.探索并证明菱形的性质定理:菱形的四条边相等.
3.探索并证明菱形的性质定理:菱形对角线互相垂直,并且每条对角线平分一组对角. 学生会从边、角、对角线、对称性去探索菱形性质,但很难想到每条对角线平分一组对角.
4.探索菱形的轴对称性. 菱形轴对称性难以理解
课时目标 可能问题 教师引导 学生活动
1.理解菱形的概念,以及菱形与平行四边形的关系. 忽视菱形作为平行四边形所具备的一般性质. 实物演示. 观察;概括菱形概念;
画一画.
2.探索并证明菱形的性质定理:菱形的四条边相等. 设计学生活动; 追问证明. 探索
证明
表达.
3.探索并证明菱形的性质定理:对角线互相垂直,并且每条对角线平分一组对角. 不能关注对角线和角之间的关系. 设计小组合作; 板书证明过程; 合作学习;
观察、猜想、验证、
证明;
归纳.
4.探索菱形的轴对称性. 菱形轴对称性难以理解. 设计学生活动. 折、剪、拼等活动探究菱形的轴对称性
基于以上分析,确定本节课的教学难点是:探索并证明菱形对角线互相垂直,并且每条对角线平分一组对角以及菱形性质的应用.
04
教学技术支持条件
PPT、菱形实物模型、菱形纸片、学生作业投影
验证
性质
概括
性质
猜想
性质
形成
概念
回顾
旧知
课前检测
储备知识
过程检测
评价目标
课后检测
目标达成
应用
性质
纳入
系统
05
教学过程设计
06
目标评价设计
证明
性质
(一)课前前测
如图,在矩形ABCD中,AC与BD 相交于点O,
(1)若AB=3,BC=4,则BD=________,AO=________.
(2)若∠AOB=500,则∠ABO=______
(3)矩形ABCD是______________对称图形.
【设计意图】唤醒学生旧知,明确研究图形的性质主要研究边、角、对角线和对称性,为本节课研究菱形性质提供方法套路.
矩形 平行四边形
图形
边
角
对角线
对称性
(二)回顾旧知
AB CD,AD BC
∠ABC=∠ADC
∠BAD=∠BCD
AO=CO,BO=DO
中心对称
同平行四边形
∠ABC=∠ADC=∠BAD
=∠BCD=900
中心对称、轴对称
特殊(角)
特殊???
AC=BD
AO=CO,BO=DO
(三)形成概念
一组邻边相等的平行四边形是菱形.
菱形:
【设计意图】通过实物演示,让学生直观感受菱形是在平行四边形基础上边的特殊化,经历概念的形成过程,理解菱形和平行四边形的关系,培养学生的几何直观.
D
C
A
B
【设计意图】让学生经历概念的理解过程,进一步理解菱形是特殊的平行四边形;同时在阐述做法时,帮助学生对定义的了解从几何直观向逻辑推理发展.
画一画:根据定义用直尺或圆规在平行四边形ABCD内画菱形ABEF,使E、F分别在BC、AD上.
【设计意图】让学生感受数学来源于生活、应用于生活,欣赏菱形所具有的工整、匀称、美观的特点,渗透美育,体现数学育人价值.
举例说说生活中哪些地方用到了菱形.
(三)猜想性质
1.观察并猜想菱形所有的性质,写在表格中;
2.小组交流,组内分享你的猜想.
【设计意图】,通过演示,引导学生类比矩形性质研究路径作出猜想、明确研究对象.
矩形 平行四边形 菱形
图形
边
角
对角线
对称性
AB CD,AD BC
∠ABC=∠ADC
∠BAD=∠BCD
AO=CO,BO=DO
中心对称
同平行四边形
∠ABC=∠ADC=∠BAD
=∠BCD=900
AC=BD
中心对称、轴对称
AO=CO,BO=DO
转化
【设计意图】在折一折通过菱形的整体把握,探索了菱形的对称性,用菱形的轴对称性验证菱形的性质;在剪一剪中由整体聚焦到局部,即将菱形转化为特殊三角形,渗透转化思想.
将菱形纸片折一折、剪一剪验证你的猜想.
(四)验证性质
在菱形ABCD中,对角线AC、BD相交于点O.
求证:AC⊥BD,AC平分∠BAD和∠BCD,
BD平分∠ABC和∠ADC.
(五)证明性质
【设计意图】在证明中体现数学的严谨性,培养学生逻辑推理能力,学生利用全等三角形或者等腰三角形三线合一来证明对角线互相垂直,通过比较来得出利用三线合一较为简洁,渗透解决方案的选择和优化,帮助学生积累数学活动经验,突破本节课的重难点.
(六)归纳性质
根据前面探究,可得到菱形哪些性质?
定理1:菱形的四条边相等.
定理2:菱形的对角线互相垂直,并且每条对角线平分一组对角.
∵菱形ABCD
∴AB=BC=CD=AD
∵菱形ABCD
∴∠1=∠2=∠3=∠4
∠5=∠6=∠7=∠8
(七)性质应用
如图,已知四边形ABCD是菱形,
(1)若BD为16,则BO为_________.
(2)若周长为 28,则边长为_________.
(3)若∠ABC=80°,则∠BDC=___________.
(4)若 AC=12,BD=16,则菱形的边长是________,面积是____________.
检测课时目标1:理解菱形的概念,
以及菱形与平行四边形的关系.
检测课时目标2:探索并证明菱形的性质定理:
菱形的四条边相等.
检测课时目标3:探索并证明菱形的性质定理
对角线互相垂直,并平分一组对角.
检测课时目标4:理解菱形的对称性.
目标检测1
【设计意图】基于测评理念,围绕本节课目标设计检测题,及时了解学生对本节课目标的达成情况,巩固菱形的性质,拓展菱形面积的计算方法,为例题中菱形性质的综合应用做铺垫.
补救4:若 AC=6,CD=5,则菱形的周长是________,面积是____________.
例题 在菱形 ABCD 中,对角线 AC 与 BD 相交于点 O,∠CBD=30°
BD=6.求菱形的边长和对角线 AC 的长.
追问1:在解决问题中用了菱形的哪些性质?
追问2:还能计算出菱形的周长或面积吗?
【设计意图】渗透从一般到特殊到更特殊的研究方法,强调书写要求,培养学生的逻辑推理能力.通过追问巩固性质,提炼解决菱形问题的一般方法即转化为特殊三角形.
如图,在菱形 ABCD 中,对角线 AC , BD 交于点 O. ∠CBD=30°,BD=6. 若点 E , F , G 分别是线段 BD ,AB ,AD 上的动点, 且满足 EF⊥AB,EG⊥AD. 思考:EF+EG 的值是否会改变?
目标检测2
【设计意图】基于测评理念,设计目标检测额,检测学生目标4理解菱形的轴对称性,培养学生灵活应用菱形性质解决问题能力,本题方法多样,其中利用菱形的轴对称性最为直观,帮助学生抓住图形本质.
菱形
平行四边形
定义
性质
矩形
转化
类比
?
【设计意图】将本节知识纳入体系,帮助学生获得系统性知识,提炼数学思想方法,为之后学习正方形以及其它图形提供方法借鉴.
课后检测
检测课时目标1
检测课时目标3
检测课时目标3
1.菱形具有而平行四边形不一定具有的性质是( )
A.对角线互相垂直 B.对边平行
C.对边相等 D.对角线互相平分
2.如图,可以使平行四边形ABCD成为菱形的条件是( )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
3.如图,已知菱形ABCD中,∠A=400,则∠ADB的度数是( )
A.400 B.500 C.600 D.700
检测课时目标4
检测课时目标2
5.已知菱形ABCD中,AB=5,AC=6,则BC边上的高为( )
A.18 B.16 C.15 D.14
4.如图,在菱形ABCD中,AC=6,BD=8,则 ABD的周长等于( )
A.4 B.8 C.4.8 D.9.6
【设计意图】基于测评理念,围绕本节课目标设计课后检测题,了解学生课堂目标达成情况,
根据测评采取补救措施.
欢迎批评指正!
5.2.1 菱形
立意素养 基于测评
说课流程
01
内容及内容解析
02
目标及目标解析
03
教学问题诊断分析
05
教学过程设计
06
目标评价设计
04
教学技术支持条件
平行四边形
矩形
正方形
定义
性质
判定
应用
角特殊
边特殊
类比
01
内容及内容解析
本节课的教学重点:探索并证明菱形的性质
类比
菱形
02
目标及目标解析
对照课标要求
课标要求 课时目标 目标解析
1.理解菱形的概念,以及菱形与平行四边形之间的关系. 2.探索并证明菱形的性质定理:菱形的四条边相等,对角线互相垂直. 3.探索菱形的轴对称性. 1.理解菱形的概念,以及菱形与平行四边形的关系. 2.探索并证明菱形的性质定理:菱形的四条边相等. 3.探索并证明菱形的性质定理:对角线互相垂直,并每条对角线平分一组对角. 4.探索菱形的轴对称性. 1.学生能说出菱形与平行四边形的关系,概括出菱形的概念(文字语言和符号语言).
2.学生能说出菱形的四条边相等,并给出证明.
3. 猜想、验证、证明、归纳出菱形对角线互相垂直,并每条对角线平分一组对角.
4.学生通过折、剪、拼明确菱形是轴对称图形,并能说出它的对称轴.
目标确定
三角形的分类和特殊三角形的性质
平行四边形和矩形的性质、判定、应用
能够从边和角考虑图形的特殊化,知道从边、角、对角线和对称性研究图形性质.
已经具备的基础
03
教学问题诊断分析
可能存在的问题
课时目标 可能问题
1.理解菱形的概念,以及菱形与平行四边形的关系. 菱形与平行四边形的关系学生难以理解.
2.探索并证明菱形的性质定理:菱形的四条边相等.
3.探索并证明菱形的性质定理:菱形对角线互相垂直,并且每条对角线平分一组对角. 学生会从边、角、对角线、对称性去探索菱形性质,但很难想到每条对角线平分一组对角.
4.探索菱形的轴对称性. 菱形轴对称性难以理解
课时目标 可能问题 教师引导 学生活动
1.理解菱形的概念,以及菱形与平行四边形的关系. 忽视菱形作为平行四边形所具备的一般性质. 实物演示. 观察;概括菱形概念;
画一画.
2.探索并证明菱形的性质定理:菱形的四条边相等. 设计学生活动; 追问证明. 探索
证明
表达.
3.探索并证明菱形的性质定理:对角线互相垂直,并且每条对角线平分一组对角. 不能关注对角线和角之间的关系. 设计小组合作; 板书证明过程; 合作学习;
观察、猜想、验证、
证明;
归纳.
4.探索菱形的轴对称性. 菱形轴对称性难以理解. 设计学生活动. 折、剪、拼等活动探究菱形的轴对称性
基于以上分析,确定本节课的教学难点是:探索并证明菱形对角线互相垂直,并且每条对角线平分一组对角以及菱形性质的应用.
04
教学技术支持条件
PPT、菱形实物模型、菱形纸片、学生作业投影
验证
性质
概括
性质
猜想
性质
形成
概念
回顾
旧知
课前检测
储备知识
过程检测
评价目标
课后检测
目标达成
应用
性质
纳入
系统
05
教学过程设计
06
目标评价设计
证明
性质
(一)课前前测
如图,在矩形ABCD中,AC与BD 相交于点O,
(1)若AB=3,BC=4,则BD=________,AO=________.
(2)若∠AOB=500,则∠ABO=______
(3)矩形ABCD是______________对称图形.
【设计意图】唤醒学生旧知,明确研究图形的性质主要研究边、角、对角线和对称性,为本节课研究菱形性质提供方法套路.
矩形 平行四边形
图形
边
角
对角线
对称性
(二)回顾旧知
AB CD,AD BC
∠ABC=∠ADC
∠BAD=∠BCD
AO=CO,BO=DO
中心对称
同平行四边形
∠ABC=∠ADC=∠BAD
=∠BCD=900
中心对称、轴对称
特殊(角)
特殊???
AC=BD
AO=CO,BO=DO
(三)形成概念
一组邻边相等的平行四边形是菱形.
菱形:
【设计意图】通过实物演示,让学生直观感受菱形是在平行四边形基础上边的特殊化,经历概念的形成过程,理解菱形和平行四边形的关系,培养学生的几何直观.
D
C
A
B
【设计意图】让学生经历概念的理解过程,进一步理解菱形是特殊的平行四边形;同时在阐述做法时,帮助学生对定义的了解从几何直观向逻辑推理发展.
画一画:根据定义用直尺或圆规在平行四边形ABCD内画菱形ABEF,使E、F分别在BC、AD上.
【设计意图】让学生感受数学来源于生活、应用于生活,欣赏菱形所具有的工整、匀称、美观的特点,渗透美育,体现数学育人价值.
举例说说生活中哪些地方用到了菱形.
(三)猜想性质
1.观察并猜想菱形所有的性质,写在表格中;
2.小组交流,组内分享你的猜想.
【设计意图】,通过演示,引导学生类比矩形性质研究路径作出猜想、明确研究对象.
矩形 平行四边形 菱形
图形
边
角
对角线
对称性
AB CD,AD BC
∠ABC=∠ADC
∠BAD=∠BCD
AO=CO,BO=DO
中心对称
同平行四边形
∠ABC=∠ADC=∠BAD
=∠BCD=900
AC=BD
中心对称、轴对称
AO=CO,BO=DO
转化
【设计意图】在折一折通过菱形的整体把握,探索了菱形的对称性,用菱形的轴对称性验证菱形的性质;在剪一剪中由整体聚焦到局部,即将菱形转化为特殊三角形,渗透转化思想.
将菱形纸片折一折、剪一剪验证你的猜想.
(四)验证性质
在菱形ABCD中,对角线AC、BD相交于点O.
求证:AC⊥BD,AC平分∠BAD和∠BCD,
BD平分∠ABC和∠ADC.
(五)证明性质
【设计意图】在证明中体现数学的严谨性,培养学生逻辑推理能力,学生利用全等三角形或者等腰三角形三线合一来证明对角线互相垂直,通过比较来得出利用三线合一较为简洁,渗透解决方案的选择和优化,帮助学生积累数学活动经验,突破本节课的重难点.
(六)归纳性质
根据前面探究,可得到菱形哪些性质?
定理1:菱形的四条边相等.
定理2:菱形的对角线互相垂直,并且每条对角线平分一组对角.
∵菱形ABCD
∴AB=BC=CD=AD
∵菱形ABCD
∴∠1=∠2=∠3=∠4
∠5=∠6=∠7=∠8
(七)性质应用
如图,已知四边形ABCD是菱形,
(1)若BD为16,则BO为_________.
(2)若周长为 28,则边长为_________.
(3)若∠ABC=80°,则∠BDC=___________.
(4)若 AC=12,BD=16,则菱形的边长是________,面积是____________.
检测课时目标1:理解菱形的概念,
以及菱形与平行四边形的关系.
检测课时目标2:探索并证明菱形的性质定理:
菱形的四条边相等.
检测课时目标3:探索并证明菱形的性质定理
对角线互相垂直,并平分一组对角.
检测课时目标4:理解菱形的对称性.
目标检测1
【设计意图】基于测评理念,围绕本节课目标设计检测题,及时了解学生对本节课目标的达成情况,巩固菱形的性质,拓展菱形面积的计算方法,为例题中菱形性质的综合应用做铺垫.
补救4:若 AC=6,CD=5,则菱形的周长是________,面积是____________.
例题 在菱形 ABCD 中,对角线 AC 与 BD 相交于点 O,∠CBD=30°
BD=6.求菱形的边长和对角线 AC 的长.
追问1:在解决问题中用了菱形的哪些性质?
追问2:还能计算出菱形的周长或面积吗?
【设计意图】渗透从一般到特殊到更特殊的研究方法,强调书写要求,培养学生的逻辑推理能力.通过追问巩固性质,提炼解决菱形问题的一般方法即转化为特殊三角形.
如图,在菱形 ABCD 中,对角线 AC , BD 交于点 O. ∠CBD=30°,BD=6. 若点 E , F , G 分别是线段 BD ,AB ,AD 上的动点, 且满足 EF⊥AB,EG⊥AD. 思考:EF+EG 的值是否会改变?
目标检测2
【设计意图】基于测评理念,设计目标检测额,检测学生目标4理解菱形的轴对称性,培养学生灵活应用菱形性质解决问题能力,本题方法多样,其中利用菱形的轴对称性最为直观,帮助学生抓住图形本质.
菱形
平行四边形
定义
性质
矩形
转化
类比
?
【设计意图】将本节知识纳入体系,帮助学生获得系统性知识,提炼数学思想方法,为之后学习正方形以及其它图形提供方法借鉴.
课后检测
检测课时目标1
检测课时目标3
检测课时目标3
1.菱形具有而平行四边形不一定具有的性质是( )
A.对角线互相垂直 B.对边平行
C.对边相等 D.对角线互相平分
2.如图,可以使平行四边形ABCD成为菱形的条件是( )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
3.如图,已知菱形ABCD中,∠A=400,则∠ADB的度数是( )
A.400 B.500 C.600 D.700
检测课时目标4
检测课时目标2
5.已知菱形ABCD中,AB=5,AC=6,则BC边上的高为( )
A.18 B.16 C.15 D.14
4.如图,在菱形ABCD中,AC=6,BD=8,则 ABD的周长等于( )
A.4 B.8 C.4.8 D.9.6
【设计意图】基于测评理念,围绕本节课目标设计课后检测题,了解学生课堂目标达成情况,
根据测评采取补救措施.
欢迎批评指正!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
