浙教版数学九年级上册 课件:1.3二次函数的性质课件(共44张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 课件:1.3二次函数的性质课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 587.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-20 17:04:32 | ||
图片预览






文档简介
课件44张PPT。根据要求填空:(2)抛物线 的顶点坐标是 ,
对称轴是 .(-2,-1)直线x=-2(3)抛物线 的顶点坐标是 ,
对称轴是 .
直线x=2(2, -1)(1)抛物线 的顶点坐标是 ,
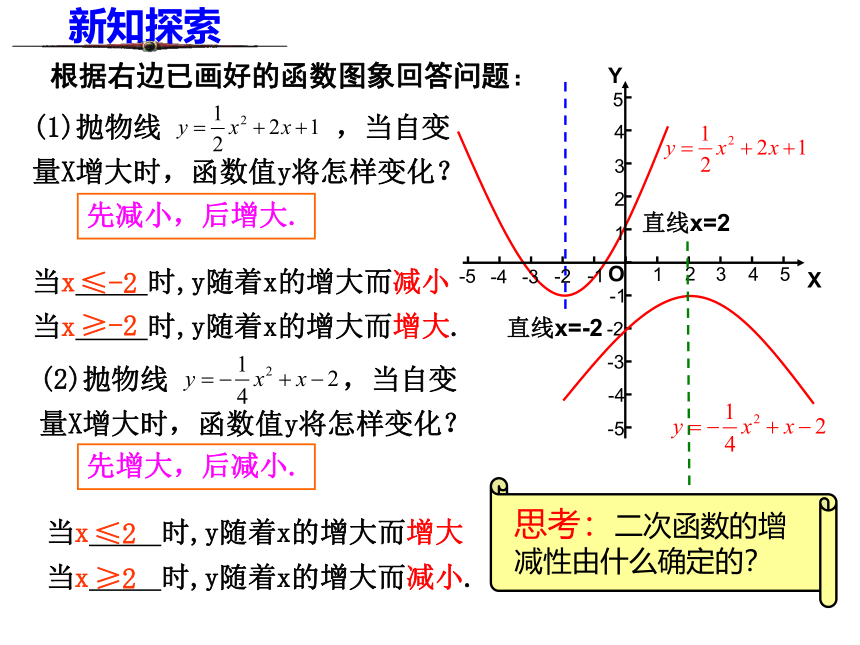
对称轴是 .课前热身根据右边已画好的函数图象回答问题:(1)抛物线 ,当自变
量X增大时,函数值y将怎样变化?(2)抛物线 ,当自变
量X增大时,函数值y将怎样变化?先减小,后增大.先增大,后减小.当x 时,y随着x的增大而减小
当x 时,y随着x的增大而增大.当x 时,y随着x的增大而增大
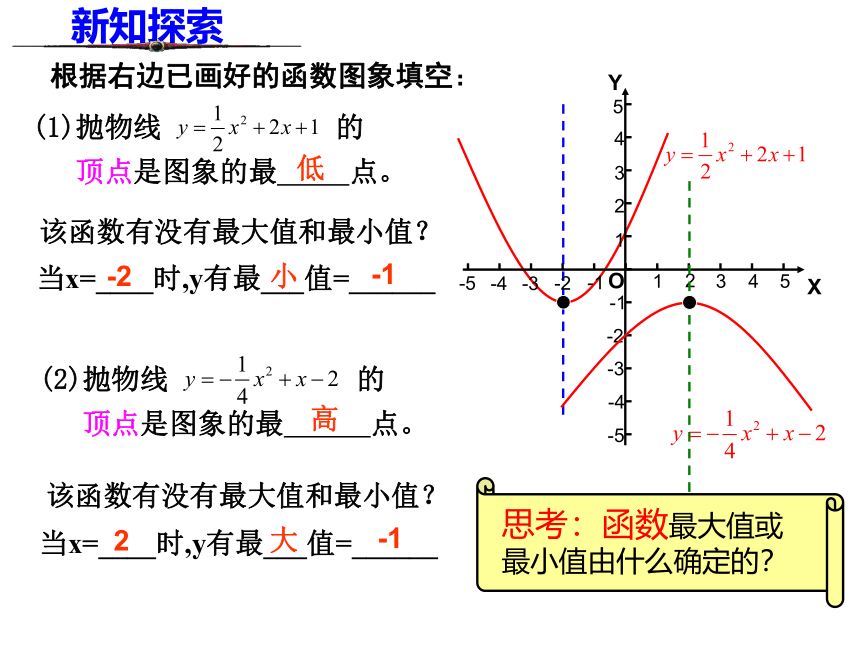
当x 时,y随着x的增大而减小.≤-2≥-2≤2≥2新知探索直线x=-2直线x=2根据右边已画好的函数图象填空:(1)抛物线 的
顶点是图象的最 点。(2)抛物线 的
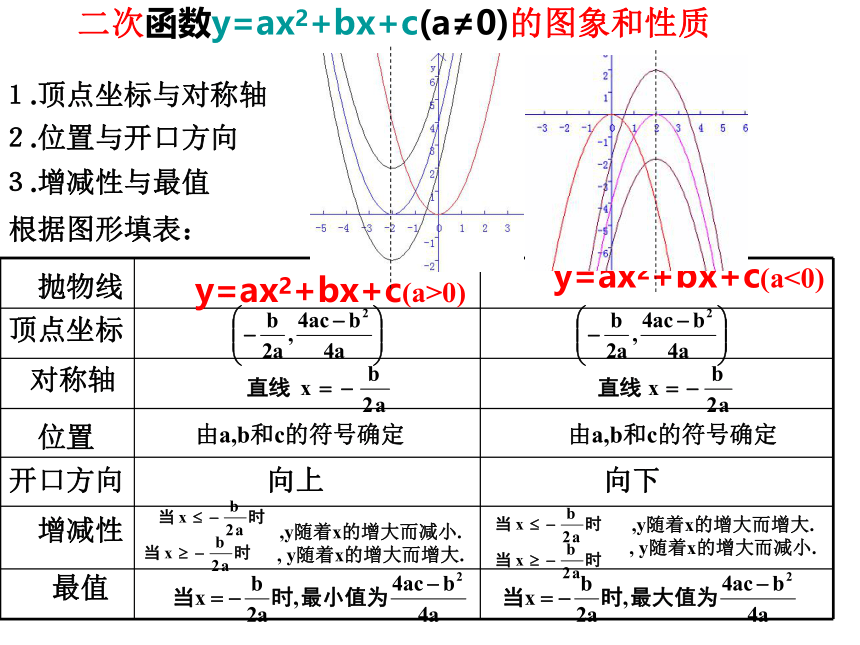
顶点是图象的最 点。该函数有没有最大值和最小值?该函数有没有最大值和最小值?当x=____时,y有最___值=______当x=____时,y有最___值=______低高-2小-12大-1新知探索二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下,y随着x的增大而减小.
, y随着x的增大而增大. ,y随着x的增大而增大.
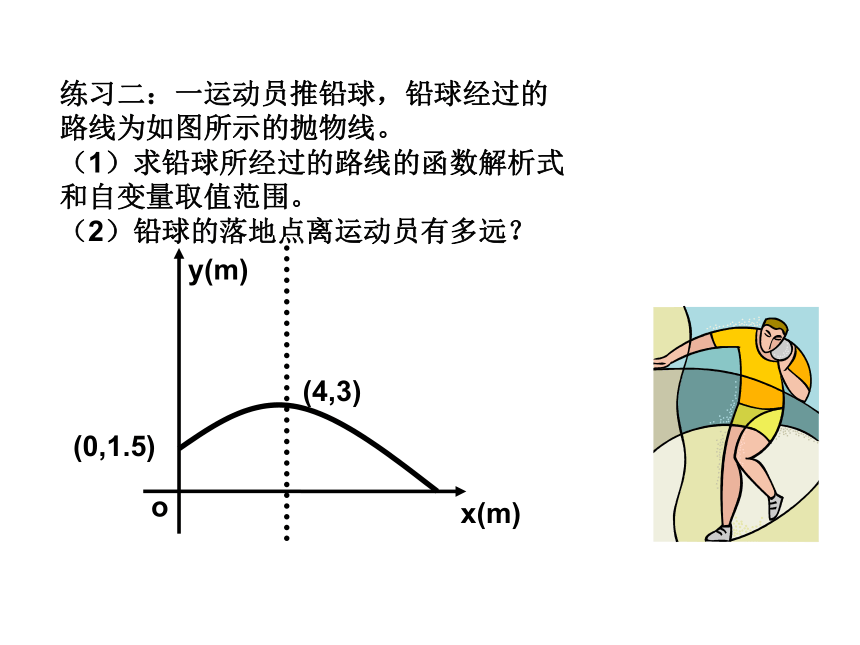
, y随着x的增大而减小. 根据图形填表:1,已知抛物线y=ax2经过点(-2,2). (1)求这条抛物线的解析式. (2)求出这个二次函数的最大值或最小值. (3)在此抛物线上有两点A(x1,y1),B(x2,y2),且x1>x2>0,试比较y1与y2的大小.综合练习练习二:一运动员推铅球,铅球经过的路线为如图所示的抛物线。 (1)求铅球所经过的路线的函数解析式和自变量取值范围。 (2)铅球的落地点离运动员有多远?y(m)(1).每个图象与x轴有几个交点?
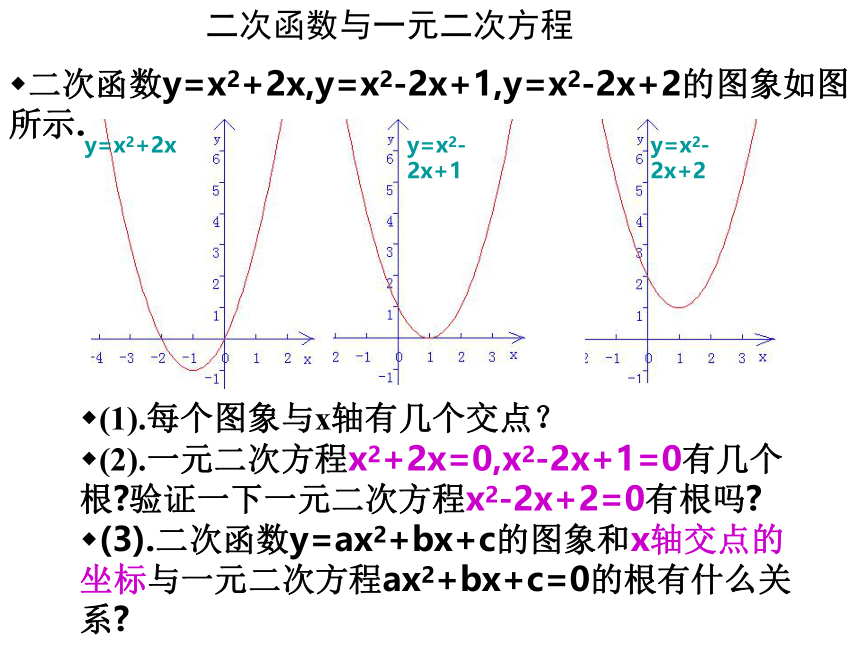
(2).一元二次方程x2+2x=0,x2-2x+1=0有几个根?验证一下一元二次方程x2-2x+2=0有根吗?
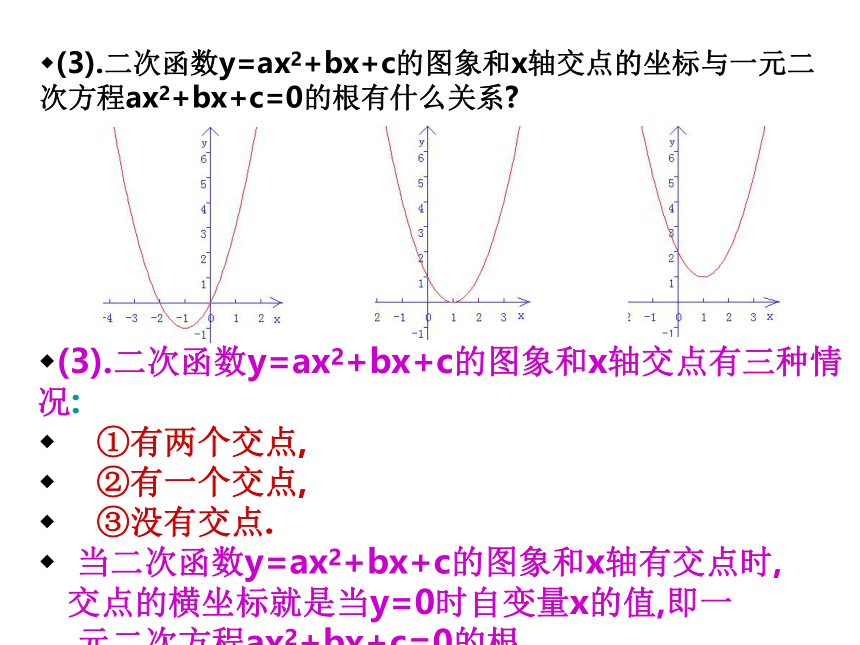
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?二次函数与一元二次方程 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.y=x2+2xy=x2-2x+1y=x2-2x+2(3).二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,
交点的横坐标就是当y=0时自变量x的值,即一
元二次方程ax2+bx+c=0的根.(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?△>0△=0
△<0OXY(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。解:∵A、B在x轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)你发现方程 的解x1、x2与A、B的坐标有什么联系?x2-3x+2=0举例:结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( ), B( )x1,0x2,0x二次函数图象y=ax2+bx+c如果图象的顶点在x轴上,则
如果图像的顶点在y轴上,则二次函数图象y=-x2+2(m-1)x+2m-m2
(1)图像关于y轴对称,则m =
(2)图像经过原点,则m=
(3)图像与坐标轴只有2个交点,则m=
( 1 )图象过A(0,1) 、B(1,2)、C(2,-1)三点 (1) 已知抛物线y=ax2+bx+c满足下列条件,求函数的解析式.(1)解:设抛物线的解析式为y=ax2+bx+c∵图象过A(0,1) 、B(1,2)、C(2,-1)三点
∴∴∴y= -2x2+3x+1求函数的解析式的几种方法(2)图象顶点是(-2,3),且经过点(-1,5)解:∵图象顶点是(-2,3)∴设其解析式为y=a(x+2)2+3∵图象经过点(-1,5)∴5=a(-1+2)2+3∴a=2∴y=2(x+2)2+3解:∵A(1,0),对称轴为x=2∴抛物线与x轴另一个交点C应为(3,0)∴设其解析式为y=a(x-1)(x-3)
∵B(0,-3)∴-3=a(0-1)(0-3)∴a= -1∴y= -(x-1)(x-3)
(3)图象经过A(1,0)、B(0,-3),且对称轴是直线x=21AB-3C34、求满足下列条件的抛物线的解析式:经过点A(2,4),B(-1,0)且在x轴上截得的线段长为2解: ∵B(-1,0)且在x轴上截得的线段长为2∴抛物线与x轴的另一个交点坐标为C(-3,0)或C’(1,0)∴设抛物线的解析式为y=a(x- x1)(x- x2)①当抛物线经过B、C两点时,解析式为y=a(x+1)(x+3)又∵抛物线经过A(2,4)∴4=a(2+1)(2+3)②当抛物线经过B、C’ 两点时,解析式为y=a(x+1)(x-1)解法同(1)B-1- 31CC’∴a=∴y= (x+1)(x+3)
例2:已知抛物线y=(x+1)2-2,将此抛物线分别作轴对称变换,请分别求出变换后的抛物线。(1)关于x轴作轴对称变换(2)关于y轴作轴对称变换.(-1,-2).(-1,2).(-1,-2).(1,-2)已知抛物线y=x2-2x-3,将其图像作以下对称,请写出对称后的抛物线。熟能生巧(1)关于x轴作轴对称变换(2)关于y轴作轴对称变换已知抛物线y=x2-2x-3,将其图像作以下对称,请写出对称后的抛物线。 (1)关于顶点中心对称(2)关于原点中心对称函数y=a(x+m)2+k
若关于顶点对称,则变为y=-a(x+m)2+k
若关于原点对称,则变为y=-a(x-m)2-k例3:.(1,-4).(1,-4).(-1,4)(1,-4).练习1、 二次函数y=ax2+bx+c的图象如图所示对称轴x=_____顶点坐标:______当x=_____时,y有最_____值是____函数值y<0时,对应x的取值范围是_______函数值y>0时,对应x的取值范围是_______
函数值y=0时,对应x的取值范围是_______
当x_______时,y随x的增大而增大.-1(-1,-2)-1 小-2-31-3或1≥-1练一练:抛物线y=ax2+bx+c如图所示,试确定a、b、c、 b2-4ac的符号:xyo练一练:已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )A、第一象限
B、第二象限
C、第三象限
D、第四象限 xoyD练习2、已知二次函数
y=ax2+bx+c的图象如图所
示,下列结论①a+ b + c<0
②a – b + c>0 ③abc>0 ④
b=2a。其中正确的结论的
个数是( )
A 1个 B 2个 C 3个 D 4个mnD已知:一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系中的大致图象是图中的( )练一练:(A)(B)(C)(D)C(-1,0)(3,0)(0,-3)数形结合(1)a >0,b < 0, c < 0.(4)对称轴:直线x = 1(5)顶点坐标(1,-4)(6)当x = 1时, y有最小值(7)当x≥1,y 随 x 增大而增大;
当x≤1 ,y 随 x 增大而减小.(2) 若A( ),B( ),C( )为二次函数 的图象上的三点,则 的大小关系是 ( ) A. B. C. D. B领略图象法的魅力数形结合转化思想当x为何值时,y1> y2 ?X<1或X>3 利用图象法
求一元二次方程x2= - 2x +3的近似解. 你会吗?根据你的图象,求当X取何值时, x2> - 2x+3你知道 的解的个数吗?4,将抛物线y=x2向下平移后,使它的顶点C与它在x轴上的两个交点A,B组成等边三角形ABC,求此抛物线的解析式.5,已知二次函数y=2x2+8mx+2m+3,如果它的图像的顶点在x轴上,求m的值和顶点坐标.6,已知抛物线y=0.25x2,把它的顶点移到x轴上的点A, 所得的抛物线与y轴交于点B,且线段OA,OB满足关系OA-1 =OB,试说明平移方法.练习一:一座拱桥的示意图如图,当水面宽12m时,桥洞顶部离水面4m。已知桥洞的拱形是抛物线,要求该抛物线的函数解析式,你认为首先要做的工作是什么?如果以水平方向为x轴,取以下三个不同的点为坐标原点:
(1)点A,(2)点B,(3)抛物线的顶点C 得的函数解析式相同吗?请试一试。哪种取法求得的函数解析式最简单?练习2、已知m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图像经过点A(m,0),B(0,n)
(1)求这个抛物线的解析式
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C,D的坐标和三角形BCD的面积提高拓展已知抛物线y=ax2+bx+c与Y轴交于点A(0,3),与X轴分别交于B(1,0),C(5,0)两点
(1)求此抛物线的解析式
(2)若点D为线段OA的一个三等份点,求直线DC的解析式
(3)若一个动点P自OA的中点M出发,先到达X轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A,求使点P运动的总路径最短的点E,F的坐标,并求出这个最短路径长3、(07.烟台)如图,已知抛物线L1∶y=x2-4的图像与x轴交于A?C两点, 中考链接(3)探索:当点B分别位于L1在x轴上?下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由?(2)若点B是抛物线L1上的一动点(B不与A?C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点定为D,求证:点D在L2上; (1)若抛物线L1与L2关于x轴对称,求L2 的解析式;
对称轴是 .(-2,-1)直线x=-2(3)抛物线 的顶点坐标是 ,
对称轴是 .
直线x=2(2, -1)(1)抛物线 的顶点坐标是 ,
对称轴是 .课前热身根据右边已画好的函数图象回答问题:(1)抛物线 ,当自变
量X增大时,函数值y将怎样变化?(2)抛物线 ,当自变
量X增大时,函数值y将怎样变化?先减小,后增大.先增大,后减小.当x 时,y随着x的增大而减小
当x 时,y随着x的增大而增大.当x 时,y随着x的增大而增大
当x 时,y随着x的增大而减小.≤-2≥-2≤2≥2新知探索直线x=-2直线x=2根据右边已画好的函数图象填空:(1)抛物线 的
顶点是图象的最 点。(2)抛物线 的
顶点是图象的最 点。该函数有没有最大值和最小值?该函数有没有最大值和最小值?当x=____时,y有最___值=______当x=____时,y有最___值=______低高-2小-12大-1新知探索二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下,y随着x的增大而减小.
, y随着x的增大而增大. ,y随着x的增大而增大.
, y随着x的增大而减小. 根据图形填表:1,已知抛物线y=ax2经过点(-2,2). (1)求这条抛物线的解析式. (2)求出这个二次函数的最大值或最小值. (3)在此抛物线上有两点A(x1,y1),B(x2,y2),且x1>x2>0,试比较y1与y2的大小.综合练习练习二:一运动员推铅球,铅球经过的路线为如图所示的抛物线。 (1)求铅球所经过的路线的函数解析式和自变量取值范围。 (2)铅球的落地点离运动员有多远?y(m)(1).每个图象与x轴有几个交点?
(2).一元二次方程x2+2x=0,x2-2x+1=0有几个根?验证一下一元二次方程x2-2x+2=0有根吗?
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?二次函数与一元二次方程 二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示.y=x2+2xy=x2-2x+1y=x2-2x+2(3).二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,
交点的横坐标就是当y=0时自变量x的值,即一
元二次方程ax2+bx+c=0的根.(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?△>0△=0
△<0OXY(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?有两个交点有两个相异的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标。解:∵A、B在x轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0) , B(2,0)你发现方程 的解x1、x2与A、B的坐标有什么联系?x2-3x+2=0举例:结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标。因此,抛物线与一元二次方程是有密切联系的。即:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与轴的两个交点坐标分别是A( ), B( )x1,0x2,0x二次函数图象y=ax2+bx+c如果图象的顶点在x轴上,则
如果图像的顶点在y轴上,则二次函数图象y=-x2+2(m-1)x+2m-m2
(1)图像关于y轴对称,则m =
(2)图像经过原点,则m=
(3)图像与坐标轴只有2个交点,则m=
( 1 )图象过A(0,1) 、B(1,2)、C(2,-1)三点 (1) 已知抛物线y=ax2+bx+c满足下列条件,求函数的解析式.(1)解:设抛物线的解析式为y=ax2+bx+c∵图象过A(0,1) 、B(1,2)、C(2,-1)三点
∴∴∴y= -2x2+3x+1求函数的解析式的几种方法(2)图象顶点是(-2,3),且经过点(-1,5)解:∵图象顶点是(-2,3)∴设其解析式为y=a(x+2)2+3∵图象经过点(-1,5)∴5=a(-1+2)2+3∴a=2∴y=2(x+2)2+3解:∵A(1,0),对称轴为x=2∴抛物线与x轴另一个交点C应为(3,0)∴设其解析式为y=a(x-1)(x-3)
∵B(0,-3)∴-3=a(0-1)(0-3)∴a= -1∴y= -(x-1)(x-3)
(3)图象经过A(1,0)、B(0,-3),且对称轴是直线x=21AB-3C34、求满足下列条件的抛物线的解析式:经过点A(2,4),B(-1,0)且在x轴上截得的线段长为2解: ∵B(-1,0)且在x轴上截得的线段长为2∴抛物线与x轴的另一个交点坐标为C(-3,0)或C’(1,0)∴设抛物线的解析式为y=a(x- x1)(x- x2)①当抛物线经过B、C两点时,解析式为y=a(x+1)(x+3)又∵抛物线经过A(2,4)∴4=a(2+1)(2+3)②当抛物线经过B、C’ 两点时,解析式为y=a(x+1)(x-1)解法同(1)B-1- 31CC’∴a=∴y= (x+1)(x+3)
例2:已知抛物线y=(x+1)2-2,将此抛物线分别作轴对称变换,请分别求出变换后的抛物线。(1)关于x轴作轴对称变换(2)关于y轴作轴对称变换.(-1,-2).(-1,2).(-1,-2).(1,-2)已知抛物线y=x2-2x-3,将其图像作以下对称,请写出对称后的抛物线。熟能生巧(1)关于x轴作轴对称变换(2)关于y轴作轴对称变换已知抛物线y=x2-2x-3,将其图像作以下对称,请写出对称后的抛物线。 (1)关于顶点中心对称(2)关于原点中心对称函数y=a(x+m)2+k
若关于顶点对称,则变为y=-a(x+m)2+k
若关于原点对称,则变为y=-a(x-m)2-k例3:.(1,-4).(1,-4).(-1,4)(1,-4).练习1、 二次函数y=ax2+bx+c的图象如图所示对称轴x=_____顶点坐标:______当x=_____时,y有最_____值是____函数值y<0时,对应x的取值范围是_______函数值y>0时,对应x的取值范围是_______
函数值y=0时,对应x的取值范围是_______
当x_______时,y随x的增大而增大.-1(-1,-2)-1 小-2-3
B、第二象限
C、第三象限
D、第四象限 xoyD练习2、已知二次函数
y=ax2+bx+c的图象如图所
示,下列结论①a+ b + c<0
②a – b + c>0 ③abc>0 ④
b=2a。其中正确的结论的
个数是( )
A 1个 B 2个 C 3个 D 4个mnD已知:一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系中的大致图象是图中的( )练一练:(A)(B)(C)(D)C(-1,0)(3,0)(0,-3)数形结合(1)a >0,b < 0, c < 0.(4)对称轴:直线x = 1(5)顶点坐标(1,-4)(6)当x = 1时, y有最小值(7)当x≥1,y 随 x 增大而增大;
当x≤1 ,y 随 x 增大而减小.(2) 若A( ),B( ),C( )为二次函数 的图象上的三点,则 的大小关系是 ( ) A. B. C. D. B领略图象法的魅力数形结合转化思想当x为何值时,y1> y2 ?X<1或X>3 利用图象法
求一元二次方程x2= - 2x +3的近似解. 你会吗?根据你的图象,求当X取何值时, x2> - 2x+3你知道 的解的个数吗?4,将抛物线y=x2向下平移后,使它的顶点C与它在x轴上的两个交点A,B组成等边三角形ABC,求此抛物线的解析式.5,已知二次函数y=2x2+8mx+2m+3,如果它的图像的顶点在x轴上,求m的值和顶点坐标.6,已知抛物线y=0.25x2,把它的顶点移到x轴上的点A, 所得的抛物线与y轴交于点B,且线段OA,OB满足关系OA-1 =OB,试说明平移方法.练习一:一座拱桥的示意图如图,当水面宽12m时,桥洞顶部离水面4m。已知桥洞的拱形是抛物线,要求该抛物线的函数解析式,你认为首先要做的工作是什么?如果以水平方向为x轴,取以下三个不同的点为坐标原点:
(1)点A,(2)点B,(3)抛物线的顶点C 得的函数解析式相同吗?请试一试。哪种取法求得的函数解析式最简单?练习2、已知m,n是方程x2-6x+5=0的两个实数根,且m<n,抛物线y=-x2+bx+c的图像经过点A(m,0),B(0,n)
(1)求这个抛物线的解析式
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C,D的坐标和三角形BCD的面积提高拓展已知抛物线y=ax2+bx+c与Y轴交于点A(0,3),与X轴分别交于B(1,0),C(5,0)两点
(1)求此抛物线的解析式
(2)若点D为线段OA的一个三等份点,求直线DC的解析式
(3)若一个动点P自OA的中点M出发,先到达X轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A,求使点P运动的总路径最短的点E,F的坐标,并求出这个最短路径长3、(07.烟台)如图,已知抛物线L1∶y=x2-4的图像与x轴交于A?C两点, 中考链接(3)探索:当点B分别位于L1在x轴上?下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由?(2)若点B是抛物线L1上的一动点(B不与A?C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点定为D,求证:点D在L2上; (1)若抛物线L1与L2关于x轴对称,求L2 的解析式;
同课章节目录
