浙教版八年级下册 6.2 反比例函数的图象和性质 课件(共18张PPT)
文档属性
| 名称 | 浙教版八年级下册 6.2 反比例函数的图象和性质 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 354.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-05 00:00:00 | ||
图片预览

文档简介
(共18张PPT)
6.2反比例函数的图象和性质
1
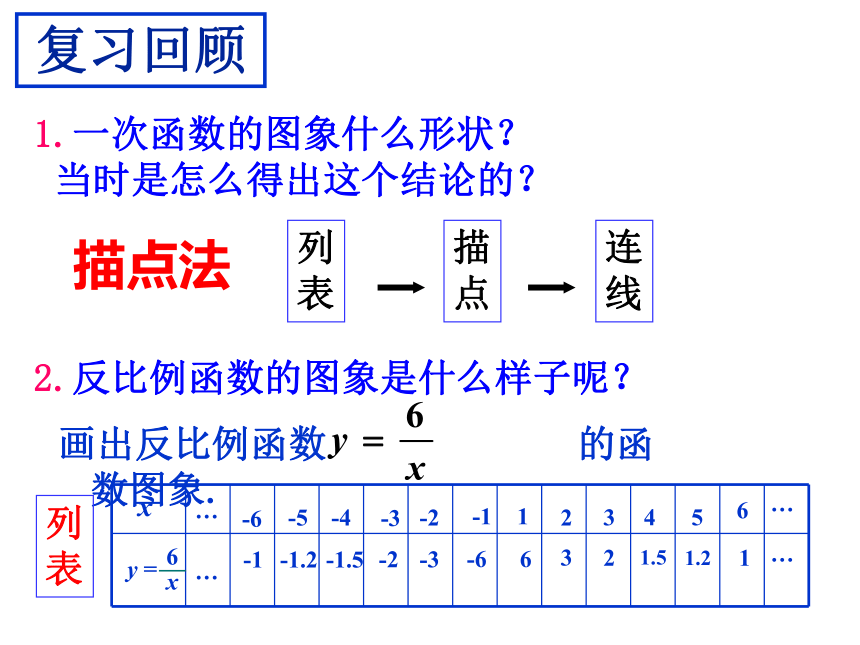
1.一次函数的图象什么形状?
2.反比例函数的图象是什么样子呢?
复习回顾
当时是怎么得出这个结论的?
描点法
列
表
描
点
连
线
画出反比例函数 的函数图象.
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
列
表
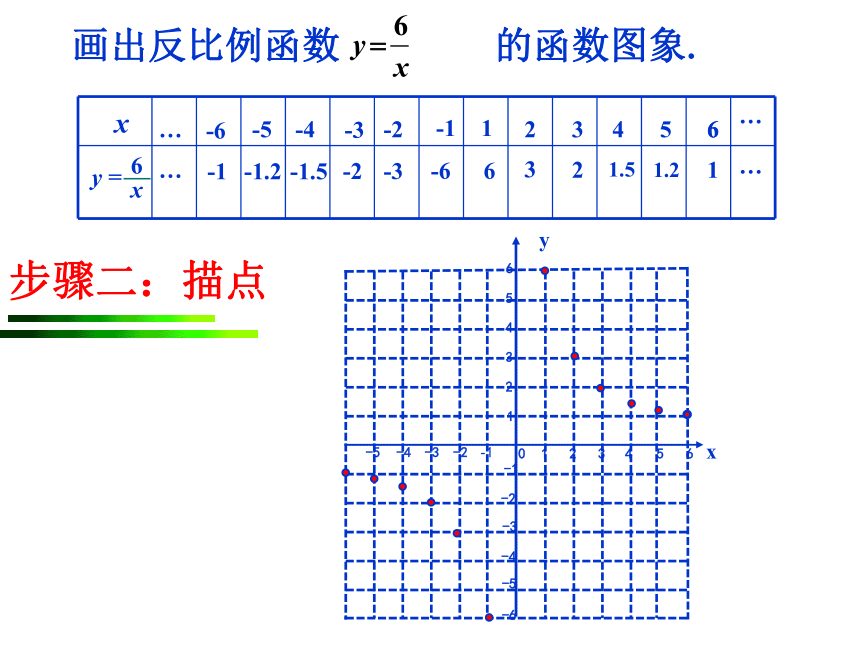
步骤二:描点
画出反比例函数 的函数图象.
1
2
3
4
5
6
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
y
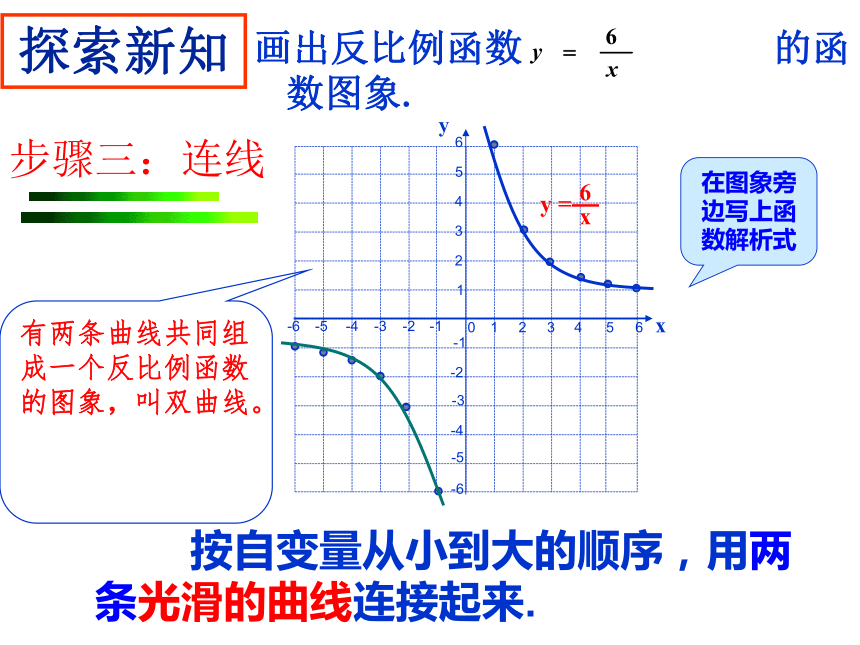
步骤三:连线
按自变量从小到大的顺序,用两条光滑的曲线连接起来.
画出反比例函数 的函数图象.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
有两条曲线共同组
成一个反比例函数
的图象,叫双曲线。
y
在图象旁边写上函数解析式
探索新知
从画反比例函数图象看,描点法还应注意什么
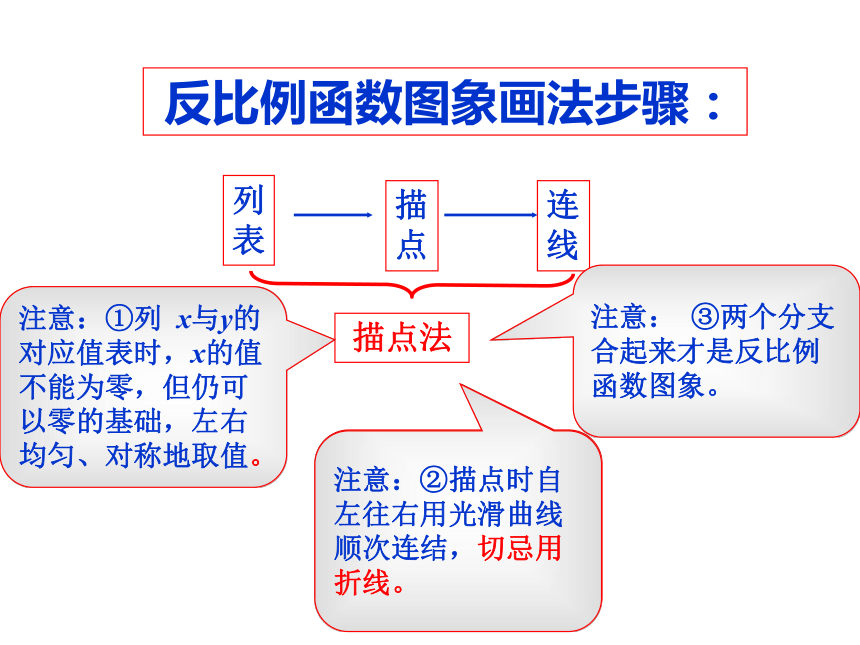
反比例函数图象画法步骤:
列
表
描
点
连
线
描点法
注意:①列 x与y的对应值表时,x的值不能为零,但仍可以零的基础,左右
均匀、对称地取值。
注意:②描点时自左往右用光滑曲线顺次连结,切忌用折线。
注意: ③两个分支合起来才是反比例函数图象。
画出反比例函数 的函数图象.
步骤一:列表
步骤二:描点
步骤三:连线
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
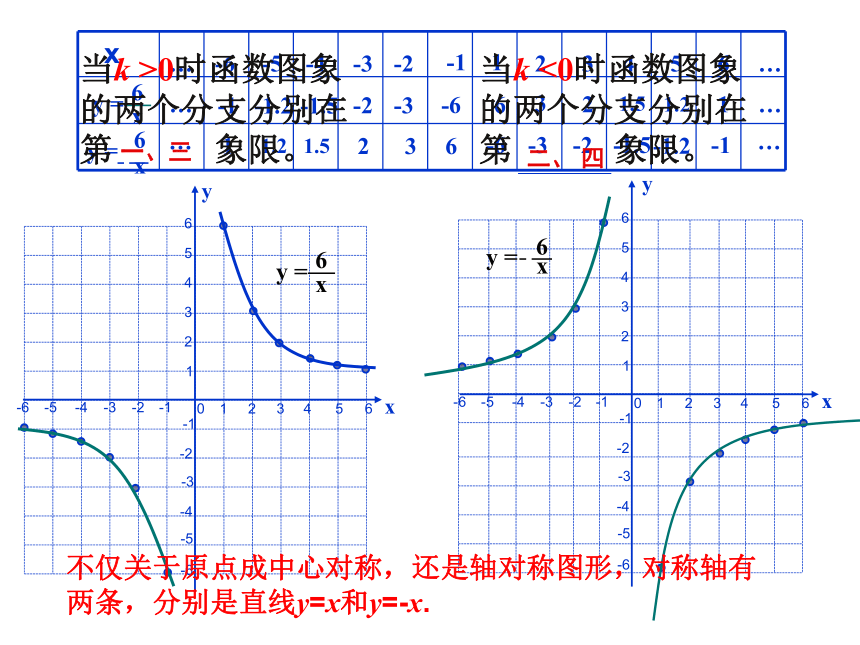
当k >0时函数图象的两个分支分别在第 象限。
一、三
当k <0时函数图象的两个分支分别在第 象限。
二、 四
不仅关于原点成中心对称,还是轴对称图形,对称轴有两条,分别是直线y=x和y=-x.
解析式:y= (k≠0)
k
x
0
x
y
当k >0时函数图象的两个分支分别在第 象限。
0
x
y
当k <0时函数图象的两个分支分别在第 象限。
一、三
二、 四
反比例函数 y = — 的图象和性质:
k
x
1.反比例函数 的图象是 。
2.性质:
(1)当 k>0 时,图象分别位于第___、___象限;
一
三
二
四
由两个分支组成的曲线
(2)反比例函数 的图象关于直角坐标系的
成 .
当 k<0 时,图象分别位于第___、___象限.
原点
中心对称
(3)双曲线的两个分支无限接近x轴和y轴,但永远不会 与x轴和y轴相交。
双曲线
归纳概括
1、函数 的图象在第__________象限,
2、函数 的图象在二、四象限,
则m的取值范围是 _______ .
3、对于函数 ,当 x<0时,图象在
第 _____象限.
二、四
m<2
三
学以致用
例1 已知反比例函数 (k≠0)的图象的一支如图。
(1)判断k是正数还是负数;
(2)求这个反比例函数的解析式;
(3)补画这个反比例函数图象的另一支。
x
0
(-4,2)
y
例题讲解
练习: 已知k<0,则函数 y1=kx, y2= 在同一坐标系中的图象大致是 ( )
x
k
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
P144课内练习2、3,作业题2、4
① 什么是反比例函数?
② 反比例函数的图象是什么样子的?怎样作图象?
③ 反比例函数的性质是什么?
课堂小结
1.反比例函数y= (k>0)在第一象限内的图像
如图所示,P为该图像上任意一点,PQ⊥x轴于Q,
设△POQ的面积为S,则S与k之间的关系是( )
k
x
P
Q
0
x
y
拓展提高
2.如图P是反比例函数y= 上一点,若图中阴影部分
的矩形面积是2,求这个反比例函数的解析式。
k
x
P
0
x
y
解:设P点坐标(x,y)
∵P点在第二象限∴x<0,y>0
∴图中阴影部分矩形的长、宽分别为-x,y 又-xy=2,∴xy=-2∵k=xy∴k=-2
∴这个反比例函数的解析式是y= -
2
x
拓展提高
任意一组变量的乘积是一个定值,即xy=k
P(m,n)
A
o
y
x
B
长方形面积 ︳m n︱ =︳k︱
三角形的面积
面积不变性
5.反比例函数 在第一象限的图
象如图所示,则k的值可能是( )
A. 4 B. 3 C. 2 D. 1
x
y
1
2
1
2
B
3.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
4.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
P
D
o
y
x
x
y
o
M
N
p
2
拓展提高
x
y
A
B
C
D
O
B
相交于A、B两点.过 A作x轴的垂线、过B
作y轴的垂线,垂足分别为D、C,设梯形ABCD的
面积为S,则( )
A.S=6 B.S=3
C.26. 如图,正比例函数 与反比例函数
6.2反比例函数的图象和性质
1
1.一次函数的图象什么形状?
2.反比例函数的图象是什么样子呢?
复习回顾
当时是怎么得出这个结论的?
描点法
列
表
描
点
连
线
画出反比例函数 的函数图象.
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
列
表
步骤二:描点
画出反比例函数 的函数图象.
1
2
3
4
5
6
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
x
y =
x
6
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
y
步骤三:连线
按自变量从小到大的顺序,用两条光滑的曲线连接起来.
画出反比例函数 的函数图象.
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y =
x
6
有两条曲线共同组
成一个反比例函数
的图象,叫双曲线。
y
在图象旁边写上函数解析式
探索新知
从画反比例函数图象看,描点法还应注意什么
反比例函数图象画法步骤:
列
表
描
点
连
线
描点法
注意:①列 x与y的对应值表时,x的值不能为零,但仍可以零的基础,左右
均匀、对称地取值。
注意:②描点时自左往右用光滑曲线顺次连结,切忌用折线。
注意: ③两个分支合起来才是反比例函数图象。
画出反比例函数 的函数图象.
步骤一:列表
步骤二:描点
步骤三:连线
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
当k >0时函数图象的两个分支分别在第 象限。
一、三
当k <0时函数图象的两个分支分别在第 象限。
二、 四
不仅关于原点成中心对称,还是轴对称图形,对称轴有两条,分别是直线y=x和y=-x.
解析式:y= (k≠0)
k
x
0
x
y
当k >0时函数图象的两个分支分别在第 象限。
0
x
y
当k <0时函数图象的两个分支分别在第 象限。
一、三
二、 四
反比例函数 y = — 的图象和性质:
k
x
1.反比例函数 的图象是 。
2.性质:
(1)当 k>0 时,图象分别位于第___、___象限;
一
三
二
四
由两个分支组成的曲线
(2)反比例函数 的图象关于直角坐标系的
成 .
当 k<0 时,图象分别位于第___、___象限.
原点
中心对称
(3)双曲线的两个分支无限接近x轴和y轴,但永远不会 与x轴和y轴相交。
双曲线
归纳概括
1、函数 的图象在第__________象限,
2、函数 的图象在二、四象限,
则m的取值范围是 _______ .
3、对于函数 ,当 x<0时,图象在
第 _____象限.
二、四
m<2
三
学以致用
例1 已知反比例函数 (k≠0)的图象的一支如图。
(1)判断k是正数还是负数;
(2)求这个反比例函数的解析式;
(3)补画这个反比例函数图象的另一支。
x
0
(-4,2)
y
例题讲解
练习: 已知k<0,则函数 y1=kx, y2= 在同一坐标系中的图象大致是 ( )
x
k
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
P144课内练习2、3,作业题2、4
① 什么是反比例函数?
② 反比例函数的图象是什么样子的?怎样作图象?
③ 反比例函数的性质是什么?
课堂小结
1.反比例函数y= (k>0)在第一象限内的图像
如图所示,P为该图像上任意一点,PQ⊥x轴于Q,
设△POQ的面积为S,则S与k之间的关系是( )
k
x
P
Q
0
x
y
拓展提高
2.如图P是反比例函数y= 上一点,若图中阴影部分
的矩形面积是2,求这个反比例函数的解析式。
k
x
P
0
x
y
解:设P点坐标(x,y)
∵P点在第二象限∴x<0,y>0
∴图中阴影部分矩形的长、宽分别为-x,y 又-xy=2,∴xy=-2∵k=xy∴k=-2
∴这个反比例函数的解析式是y= -
2
x
拓展提高
任意一组变量的乘积是一个定值,即xy=k
P(m,n)
A
o
y
x
B
长方形面积 ︳m n︱ =︳k︱
三角形的面积
面积不变性
5.反比例函数 在第一象限的图
象如图所示,则k的值可能是( )
A. 4 B. 3 C. 2 D. 1
x
y
1
2
1
2
B
3.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
4.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
P
D
o
y
x
x
y
o
M
N
p
2
拓展提高
x
y
A
B
C
D
O
B
相交于A、B两点.过 A作x轴的垂线、过B
作y轴的垂线,垂足分别为D、C,设梯形ABCD的
面积为S,则( )
A.S=6 B.S=3
C.2
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
