浙教版九年级上册 1.3 二次函数的性质 课件（51张PPT）

(共51张PPT)
1.3 二次函数的性质
复习回顾
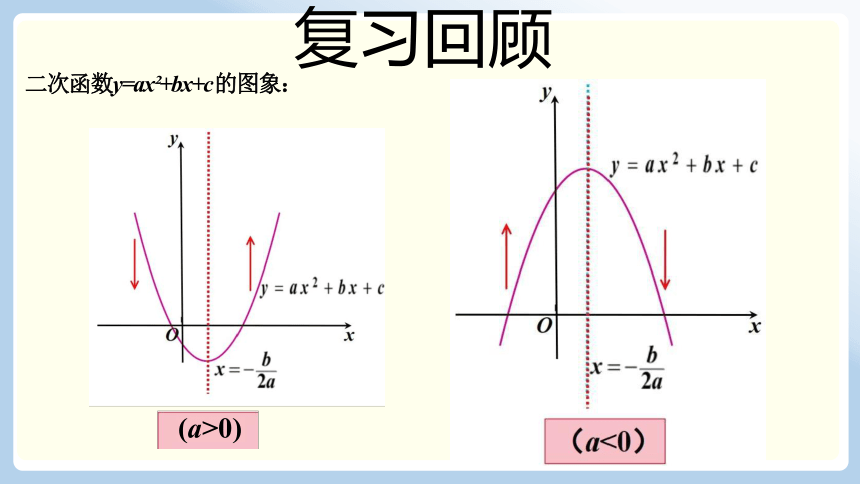
二次函数y=ax +bx+c 的图象：
(a>0)
(a>0)
讲授新知
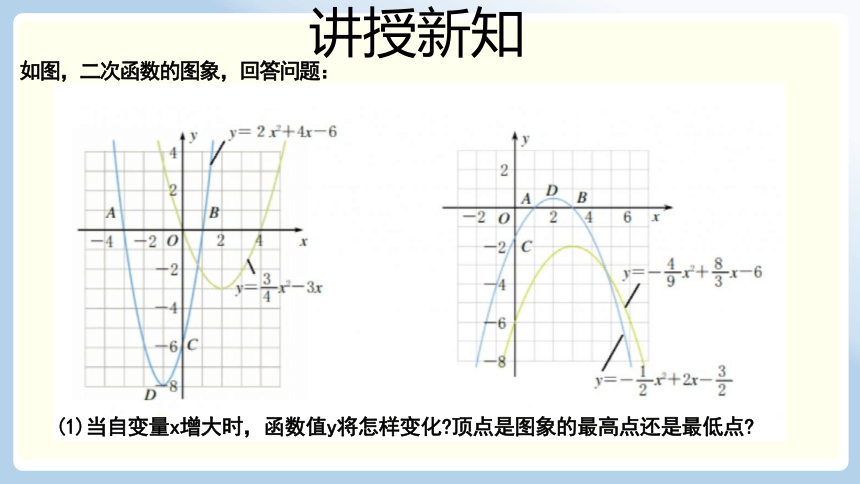
如图，二次函数的图象，回答问题：
(1)当自变量x增大时，函数值y将怎样变化 顶点是图象的最高点还是最低点
讲授新知
当 x≤2时，y随着x的增大而增大；
当 x ≥2 时， y随着x的增大而减小.
(1)当自变量x增大时，函数值y将怎样变化 顶点是图象的最高点还是最低点
顶点是图象的最高点
先增大
后减小
讲授新知
当x≤1时，y随着x的增大而减小
当x≥1时 ，y随着x的增大而增大.
(1)当自变量x增大时，函数值y将怎样变化 顶点是图象的最高点还是最低点
顶点是图象的最低点
y=2x +4x-6
先减小
后增大
讲授新知
(2)判别这些函数有没有最大值或最小值，这是由表达式中哪一个系数决定的
图1 –
当x=2 时，y 有最大值 = 当x=-1 时，y有最小值=-8
系数a
讲授新知
二次函数y=ax +bx+c(a≠0)的性质
a＞0 a＜0
开口方向 向上 向下
顶点坐标 对称轴 直线 增减性 当时，的增大而减小 当时，的增大而增大 当时，的增大而增大
当时，的增大而减小
最值 当时，最小值为 当时，最大值为
例、已知函数.
(1)求函数图象的顶点坐标、对称轴，以及图象与坐标 轴的交点坐标，
并画出函数的大致图象。
(2)自变量x在什么范围内时， y 随x的增大而增大 何 时y随x的增大而减小 并求出函数的最大值或最小值。
思考
方程ax +bx+c=0(a≠0)与函数y=ax +bx+c(a≠0)有什么关系
一般地，从二次函数y=ax +bx+c的图象可得如下结论：
如果抛物线y=ax +bx+c与x轴有公共点，公共点的横坐标为xo, 那么当x=xo时，函数值是0,因此x=xo是
方程ax +bx+c=0的一个根.
思考
方程ax +bx+c=0(a≠0)与函数y=ax +bx+c(a≠0)有什么关系
二次函数y=ax +bx+c的图象 与x轴交点 一元二次方程x +bx+c=0的根
b -4ac
有两个交点 有两个不相等的实数根 b -4ac>0
有一个交点 有两个相等的实数根 b -4ac=0
没有交点 没有实数根 b -4ac<0
练习
1.观察图象(如图)填空：
(1)二次函数y=x +x-2的图象与x轴有 个交点，
则一元二次方程x +x-2=0的根的判别式b -4ac 0;
(2)二次函数y =x - 6x+9的图象与x轴有 个交点，
则一元二次方程x -6x+9=0的根的判别式b -4ac 0;
(3)二次函数y =x -x+1的图象与x轴 公共点，则一元二次方程x -x+1=0的根的判别式b -4ac 0.
第1章 二次函数
1.3 二次函数的性质
知识要点分类练
规律方法综合练
拓广探究创新练
知识点1 二次函数的最值
1.（2021绍兴）关于二次函数 的最大值或最小值，下列说法正确的是( )
D
A. 有最大值4 B. 有最小值4
C. 有最大值6 D. 有最小值6
[解析] 二次函数 中 ，
该函数图象开口向上，有最小值，当 时，取得最小值6.
2.当二次函数 取最小值时对应的自变量 的值为( )
A
A. B. 1 C. 2 D. 9
[解析] 将二次函数 配方可得 ,所以当 时 取得最小值5.故选A.
3.若二次函数 有最大值6，则实数 的值是_ ___.

4.如图所示，已知二次函数 的
图象经过 ， 两点.
（1） 求这个二次函数的表达式；
解：把 , 代入 ，得 解得
这个二次函数的表达式为 .
（2） 若该函数自变量的取值范围是 ，求函数的最大值和最小值.
解： ,
函数图象的顶点坐标为 .
当 时, ;
当 时, .
若该函数自变量的取值范围是 ,
则当 时，函数取得最大值2；
当 时，函数取得最小值 .
知识点2 二次函数的增减性
5.（1） 关于二次函数 ，当 _____时， 随 的增大而减小；当 _____时， 随 的增大而增大；当 ___时，函数取得最____值为___.


1
小
6
（2） 关于二次函数 ，当 ______时， 随 的增大而减小；当 ______时， 随 的增大而增大；当 ____时，函数取得最____值为___.



大
6
6. 已知抛物线 （ ， ， 为常数）， ， ， 是抛物线上的三点，则 ， ， 由小到大依次排列为_____________.（用“ ”连接）
[解析] 抛物线 （ ， ， 为常数）的对称轴为直线 ，所以点 关于对称轴直线 对称的点为 ，在对称轴右侧, 随 的增大而增大.
因为 ，所以 .
[答案]
7.已知二次函数 .
（1） 求二次函数图象的顶点坐标、对称轴及函数的最值；
解：因为 ,所以二次函数图象的顶点坐标为 ，对称轴为直线 ，函数的最小值为 .
（2） 当 在什么范围内时， 随 的增大而减小？
解：当 时， 随 的增大而减小.
知识点3 二次函数图象与坐标轴的交点
8.抛物线 与 轴的交点坐标是__________________；与 轴的交点坐标是______.
和

9.已知抛物线 .
（1） 用配方法求出它的对称轴和顶点坐标；
解： ，
对称轴是直线 ，
顶点坐标是 .
（2） 求出它与 轴的交点坐标和与 轴的交点坐标；
解：令 ，则 ，
抛物线 与 轴的交点坐标为 ；
令 ，则 ，
解得 .
抛物线 与 轴的交点坐标为 ， .
（3） 当 为何值时， 有最大值或最小值 求出最大值或最小值.
解： ，
抛物线开口向下， 有最大值.
又 抛物线的顶点坐标是 ，
当 时， 有最大值，最大值为4.
10.某广场有一喷水池，水从地面喷出（如图1-3-2所示），以水平地面为 轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线 的一部分，则水喷出的最大高度是( )
A. 4米 B. 3米 C. 2米 D. 1米
[解析] 水在空中划出的曲线是抛物线 的一部分，
水喷出的最大高度就是水在空中划出的抛物线 的顶点的纵坐标.
，
抛物线的顶点坐标为 ，故水喷出的最大高度为2米.
[答案] C
11.若一次函数 的图象过第一、三、四象限，则二次函数 ( )
A. 有最大值 B. 有最大值
C. 有最小值 D. 有最小值
[解析] 因为一次函数 的图象过第一、三、四象限，所以 因此 .因为 ，所以二次函数有最大值 .
[答案] B
12.（2022诸暨期末）已知抛物线 的对称轴为直线 ，且与 轴有两个交点，其中一个交点坐标为 ，则另一个交点坐标为______.

[解析] 点 关于直线 的对称点的坐标是 ，所以抛物线与 轴的另一个交点坐标为 .
13.已知 ， ， 为实数，点 ， 在二次函数 的图象上，则 ， 的大小关系是 ___ （用“ ”或“ ”填空）.
[解析] 易知抛物线 的对称轴为直线 ,
点 , 在对称轴的右侧.
, 抛物线开口向上,
在对称轴右侧， 随 的增大而增大.
又 ， .
[答案]
14.（2022丽水改编）［几何直观］如图1-3-3，已知点 ， 在二次函数 的图象上，且 .
（1） 若二次函数的图象经过点 .
① 这个二次函数的表达式为_________________；
[解析] 二次函数 的图象经过点 ，
，解得 ，
二次函数的表达式为 .
故答案为 .
[答案]
② 若 ，求函数图象的顶点到直线 的距离.
解： ，
点 ， 关于抛物线的对称轴对称.
由二次函数的表达式为 ，可知函数图象的对称轴是直线 ，顶点坐标为 ，
.
又 ，
， .
当 时， ，
当 时，函数图象的顶点到直线 的距离 .
图1-3-3
（2） 当 时，二次函数的最大值与最小值的差为1，点 ， 在对称轴的异侧，求 的取值范围.
解： 点 , 在对称轴的异侧，
当 时，二次函数 的最小值为 .
由题意，得二次函数图象的对称轴为直线 ,
, .
, ,
,解得 ,
.
分以下两种情况：
若 ，
则 ，
解得 ，则 .
当 时，函数的最大值为 ，最小值为 ，最大值与最小值的差为1，
， .
,
， .
若 ，
则 ，
解得 ,则 .
当 时，函数的最大值为 ，最小值为 ，
最大值与最小值的差为1，
， .
，
， .
综上所述， 的取值范围为 .