浙教版数学八年级下册 第六章 反比例函数 专题复习课件(共15张PPT)
文档属性
| 名称 | 浙教版数学八年级下册 第六章 反比例函数 专题复习课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 63.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-06 12:01:36 | ||
图片预览






文档简介
(共15张PPT)
反比例函数复习
——反比例函数中图形的面积问题
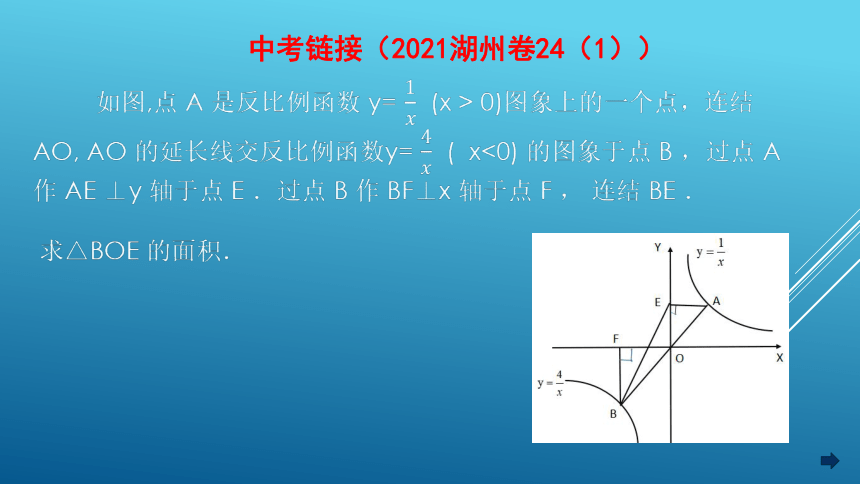
如图,点 A 是反比例函数 y= (x > 0)图象上的一个点,连结 AO, AO 的延长线交反比例函数y= ( x<0) 的图象于点 B ,过点 A 作 AE ⊥y 轴于点 E .过点 B 作 BF⊥x 轴于点 F , 连结 BE .
求△BOE 的面积.
中考链接(2021湖州卷24(1))
一、模型溯源
比例系数K的几何意义
二、模型再构
图1
图2
图3
二、模型再构
如图,若点A、B分别在反比例函数
二、模型再构
(1)如图,应用获得的经验,分别求出四个图形中阴影部分的面积。
(4)
(3)
(2)
(1)
平行转化
割补转化
和差转化
三、方法延伸
(2)如图,应用获得的经验,如何转化计算的面积。
M
N
(a,b)
(m,n)
三、方法延伸
四、模型应用
应用1:如图,直线l和双曲线y= (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1,△BOD的面积为S2,△POE的面积为S3,则( ).
A.S1<S2<S3 B.S1>S2>S3
C.S1=S2>S3 D.S1=S2<S3
应用2:如图,点B在反比例函数 ( x>0)的图象上,点C在反比例函
数 ( x>0)的图象上,且 轴, ,垂足为点C,交y轴于
点A,则的△ABC面积为 .
四、模型应用
应用3:已知,如图所示,AB⊥x轴于点A,AB交反比例函数y=(x<0)
的图象于点C,且AC∶BC=1∶3.若=4,则k的值为 .
四、 模型应用
应用4:如图,点 A 是反比例函数 y= (x > 0)图象上的一个点,连结 AO, AO 的延长线交反比例函数y= ( x<0) 的图象于点 B ,过点 A 作 AE ⊥y 轴于点 E .过点 B 作 BF⊥x 轴于点 F , 连结 BE .
求△BOE 的面积.
四、模型应用
应用5::如图,已知在平面直角坐标系中,点 A 在 x 轴负半轴 上,点 B 在第二象限内,反比例函数 y=的图象经过△OAB 的顶点 B 和边 AB 的中点 C,如果△OAB 的面积为 6,求 k 的值.
四、模型应用
五、课堂小结
通过本节课的学习,你掌握了哪些解题的策略和方法?
基本图形
平行转化
对称转化
和差转化
割补转化
图形面积
谢谢大家!
反比例函数复习
——反比例函数中图形的面积问题
如图,点 A 是反比例函数 y= (x > 0)图象上的一个点,连结 AO, AO 的延长线交反比例函数y= ( x<0) 的图象于点 B ,过点 A 作 AE ⊥y 轴于点 E .过点 B 作 BF⊥x 轴于点 F , 连结 BE .
求△BOE 的面积.
中考链接(2021湖州卷24(1))
一、模型溯源
比例系数K的几何意义
二、模型再构
图1
图2
图3
二、模型再构
如图,若点A、B分别在反比例函数
二、模型再构
(1)如图,应用获得的经验,分别求出四个图形中阴影部分的面积。
(4)
(3)
(2)
(1)
平行转化
割补转化
和差转化
三、方法延伸
(2)如图,应用获得的经验,如何转化计算的面积。
M
N
(a,b)
(m,n)
三、方法延伸
四、模型应用
应用1:如图,直线l和双曲线y= (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1,△BOD的面积为S2,△POE的面积为S3,则( ).
A.S1<S2<S3 B.S1>S2>S3
C.S1=S2>S3 D.S1=S2<S3
应用2:如图,点B在反比例函数 ( x>0)的图象上,点C在反比例函
数 ( x>0)的图象上,且 轴, ,垂足为点C,交y轴于
点A,则的△ABC面积为 .
四、模型应用
应用3:已知,如图所示,AB⊥x轴于点A,AB交反比例函数y=(x<0)
的图象于点C,且AC∶BC=1∶3.若=4,则k的值为 .
四、 模型应用
应用4:如图,点 A 是反比例函数 y= (x > 0)图象上的一个点,连结 AO, AO 的延长线交反比例函数y= ( x<0) 的图象于点 B ,过点 A 作 AE ⊥y 轴于点 E .过点 B 作 BF⊥x 轴于点 F , 连结 BE .
求△BOE 的面积.
四、模型应用
应用5::如图,已知在平面直角坐标系中,点 A 在 x 轴负半轴 上,点 B 在第二象限内,反比例函数 y=的图象经过△OAB 的顶点 B 和边 AB 的中点 C,如果△OAB 的面积为 6,求 k 的值.
四、模型应用
五、课堂小结
通过本节课的学习,你掌握了哪些解题的策略和方法?
基本图形
平行转化
对称转化
和差转化
割补转化
图形面积
谢谢大家!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
