浙教版数学九年级上册 4.3 相似三角形 课件(共15张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 4.3 相似三角形 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 492.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 07:10:04 | ||
图片预览



文档简介
(共15张PPT)
相似图形
相似图形
相似图形
4.3相似三角形
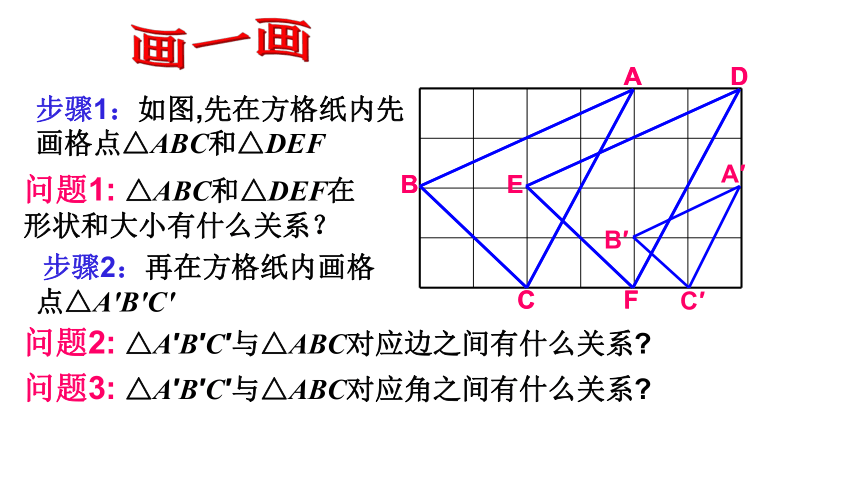
步骤1:如图,先在方格纸内先画格点△ABC和△DEF
问题1: △ABC和△DEF在形状和大小有什么关系?
问题2: △A′B′C′与△ABC对应边之间有什么关系
画一画
C
A
B
B′
A′
C′
F
D
E
步骤2:再在方格纸内画格点△A'B'C'
问题3: △A′B′C′与△ABC对应角之间有什么关系
C
A
B
F
D
E
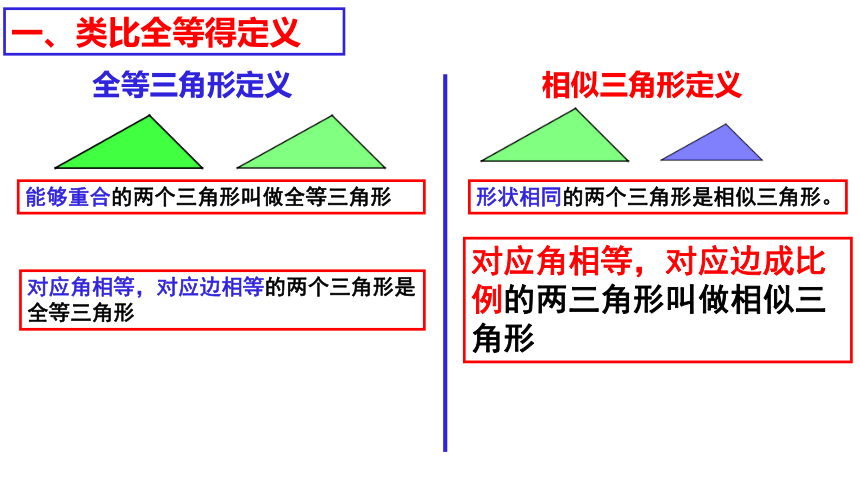
能够重合的两个三角形叫做全等三角形
对应角相等,对应边相等的两个三角形是全等三角形
形状相同的两个三角形是相似三角形。
对应角相等,对应边成比例的两三角形叫做相似三角形
全等三角形定义
相似三角形定义
一、类比全等得定义
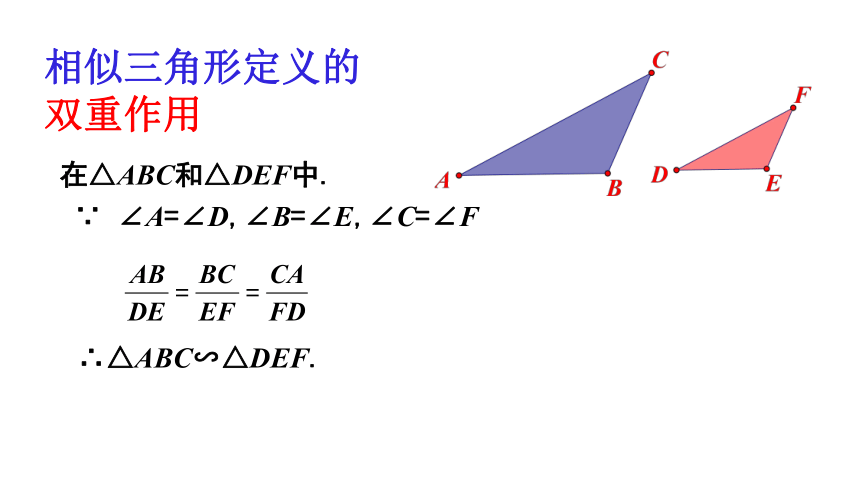
∵ ∠A=∠D,∠B=∠E,∠C=∠F
∴△ABC∽△DEF.
相似三角形定义的
双重作用
在△ABC和△DEF中.
1.两个全等三角形一定相似.( )
2.两个直角三角形一定相似.( )
3.两个等腰三角形一定相似.( )
5.两个等腰直角三角形一定相似.( )
4.两个等边三角形一定相似.( )
√
×
×
√
√
根据定义判一判
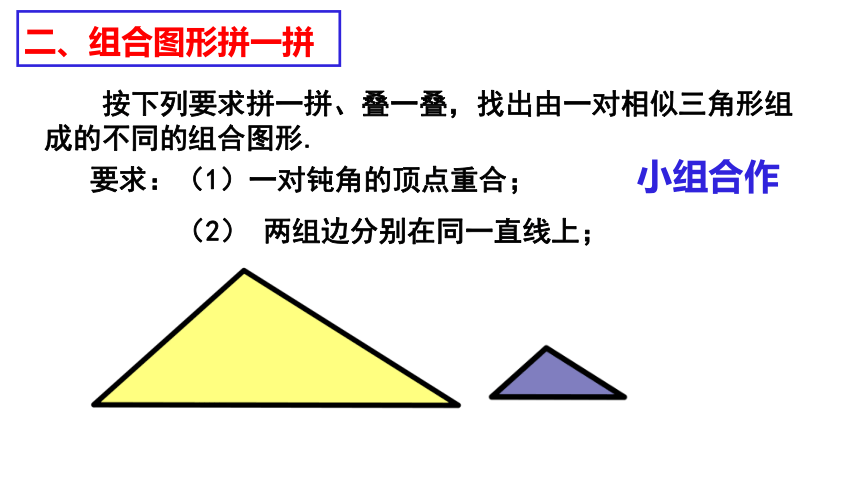
按下列要求拼一拼、叠一叠,找出由一对相似三角形组成的不同的组合图形.
要求:(1)一对钝角的顶点重合;
(2) 两组边分别在同一直线上;
二、组合图形拼一拼
小组合作
你说我听找对应
(1)
(2)
(4)
(3)
例1 已知如图,D、E分别是AB、AC边的中点.
求证:△ADE∽△ABC.
三、应用定义来解题
例2
如图,点D、E分别为△ABC的AB、AC边上的点,且△ADE∽△ABC.已知AD:DB=1:2,BC=6cm,求DE的长.
关键:对应准确
三、应用定义来解题
1.如图,两个三角形相似,c表示已知数.则α= , x =_______.
3
5
2.如图,△ADE∽△ACB.若∠ADE=∠C,AD=2cm,DB=4cm,AC=10cm,则AE=____cm.
(1)
(2)
三、应用定义来解题
3
5
如图,△ABC ∽△ACD相似,点D在AB上,已知AD=2cm,BD=2.5cm,求AC的长.
四、拓展延伸提能力
1.已知△ABC与△DEF相似, △ABC的三边2,3,4, △DEF的最大边为8,求其余两边.
2.已知△ABC与△DEF相似, △ABC的三边2,3,4, △DEF的一边为8,求其余两边.
四、拓展延伸提能力
1、这堂课学习了哪些主要内容?
2、这堂课学到了哪些方法?
3、这堂课中哪些活动经验对你有启示?
五、梳理概括想一想
定义
基本图形
性质
应用
利用性质求边角
对应角相等,对应边成比例的两个三角形
六、知识概括形成“线”
判定
利用定义证相似
双重作用
相似图形
相似图形
相似图形
4.3相似三角形
步骤1:如图,先在方格纸内先画格点△ABC和△DEF
问题1: △ABC和△DEF在形状和大小有什么关系?
问题2: △A′B′C′与△ABC对应边之间有什么关系
画一画
C
A
B
B′
A′
C′
F
D
E
步骤2:再在方格纸内画格点△A'B'C'
问题3: △A′B′C′与△ABC对应角之间有什么关系
C
A
B
F
D
E
能够重合的两个三角形叫做全等三角形
对应角相等,对应边相等的两个三角形是全等三角形
形状相同的两个三角形是相似三角形。
对应角相等,对应边成比例的两三角形叫做相似三角形
全等三角形定义
相似三角形定义
一、类比全等得定义
∵ ∠A=∠D,∠B=∠E,∠C=∠F
∴△ABC∽△DEF.
相似三角形定义的
双重作用
在△ABC和△DEF中.
1.两个全等三角形一定相似.( )
2.两个直角三角形一定相似.( )
3.两个等腰三角形一定相似.( )
5.两个等腰直角三角形一定相似.( )
4.两个等边三角形一定相似.( )
√
×
×
√
√
根据定义判一判
按下列要求拼一拼、叠一叠,找出由一对相似三角形组成的不同的组合图形.
要求:(1)一对钝角的顶点重合;
(2) 两组边分别在同一直线上;
二、组合图形拼一拼
小组合作
你说我听找对应
(1)
(2)
(4)
(3)
例1 已知如图,D、E分别是AB、AC边的中点.
求证:△ADE∽△ABC.
三、应用定义来解题
例2
如图,点D、E分别为△ABC的AB、AC边上的点,且△ADE∽△ABC.已知AD:DB=1:2,BC=6cm,求DE的长.
关键:对应准确
三、应用定义来解题
1.如图,两个三角形相似,c表示已知数.则α= , x =_______.
3
5
2.如图,△ADE∽△ACB.若∠ADE=∠C,AD=2cm,DB=4cm,AC=10cm,则AE=____cm.
(1)
(2)
三、应用定义来解题
3
5
如图,△ABC ∽△ACD相似,点D在AB上,已知AD=2cm,BD=2.5cm,求AC的长.
四、拓展延伸提能力
1.已知△ABC与△DEF相似, △ABC的三边2,3,4, △DEF的最大边为8,求其余两边.
2.已知△ABC与△DEF相似, △ABC的三边2,3,4, △DEF的一边为8,求其余两边.
四、拓展延伸提能力
1、这堂课学习了哪些主要内容?
2、这堂课学到了哪些方法?
3、这堂课中哪些活动经验对你有启示?
五、梳理概括想一想
定义
基本图形
性质
应用
利用性质求边角
对应角相等,对应边成比例的两个三角形
六、知识概括形成“线”
判定
利用定义证相似
双重作用
同课章节目录
