浙教版数学八年级下册 课件:5.3《正方形》(共22张PPT)
文档属性
| 名称 | 浙教版数学八年级下册 课件:5.3《正方形》(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 967.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-24 14:49:59 | ||
图片预览







文档简介
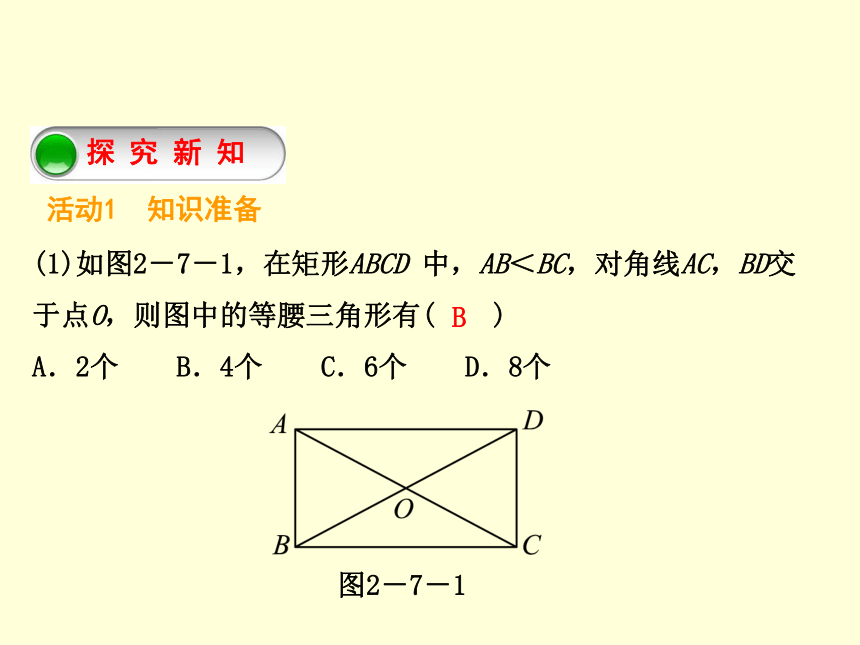
课件22张PPT。正方形2.7 正方形活动1 知识准备 B 2.7 正方形(2)①有一组________相等的平行四边形是菱形.
②菱形的四条边都______,菱形的对角线互相____________,且每条对角线平分一组对角.
③菱形的面积等于两条______________乘积的一半. 邻边 相等 垂直平分 对角线长度 2.7 正方形活动2 教材导学 是 是 是 2.7 正方形(2)与矩形比较,裁下的部分有四条边__________的特殊性质,与菱形比较,裁下的部分有四个角____________的特殊性质.
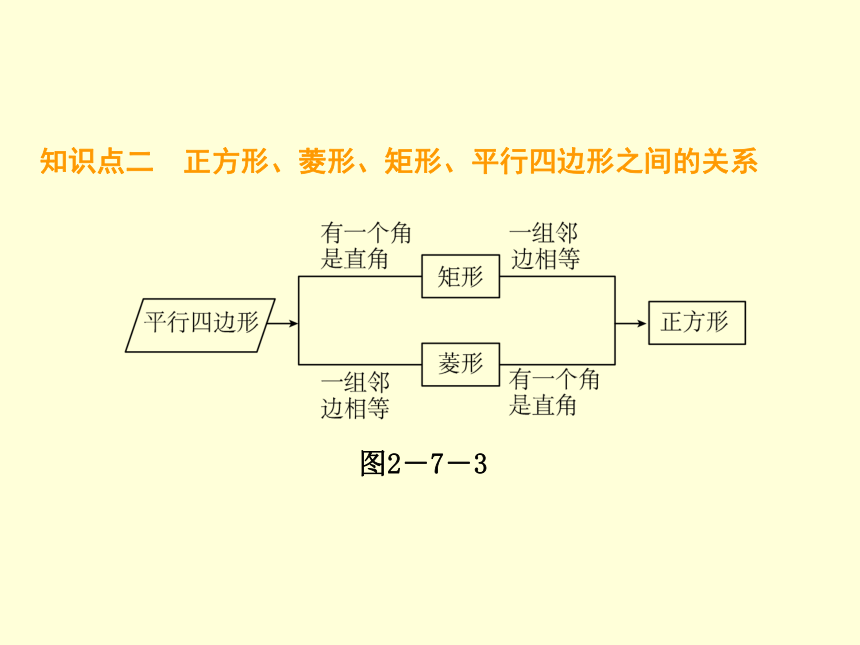
(3)结合小学学过的知识,你认为裁下的部分是________形. 都相等 都为直角 正方 ◆知识链接——[新知梳理]知识点三、四 2.7 正方形知识点一 正方形的定义 把一组____________且有一个角是________的平行四边形叫作正方形. 邻边相等 直角 2.7 正方形知识点二 正方形、菱形、矩形、平行四边形之间的关系 2.7 正方形知识点三 正方形的性质 1.四条边__________,四个角都是________;
2.对角线相等且互相____________,每条对角线平分一组对角;
3.是中心对称图形,对角线的交点是____________;
4.是轴对称图形,______________所在直线,以及过每一组对边中点的直线都是它的对称轴. 都相等 直角 垂直平分 对称中心 两条对角线 2.7 正方形知识点四 正方形的判定 在判定正方形时,通常先判定它是矩形或菱形,然后通过下列定理判定其为正方形:
1.有一组邻边相等的矩形是正方形;
2.对角线____________的矩形是正方形;
3.有一个角是直角的菱形是正方形;
4.对角线________的菱形是正方形. 互相垂直 相等 2.7 正方形探究问题一 正方形的性质 2.7 正方形2.7 正方形2.7 正方形解:(1)AD与CF还相等.
理由:∵四边形ODEF,四边形ABCO均为正方形,
∴∠DOF=∠COA=90°,DO=OF,CO=OA,
∴∠COF=∠AOD,
∴△COF≌△AOD(SAS),∴AD=CF. 2.7 正方形2.7 正方形[归纳总结] 正方形是特殊的菱形、矩形,所以正方形具有菱形、矩形的所有性质,理所当然地,正方形具有平行四边形的所有性质.正方形的性质常与全等三角形以及后面要学的相似三角形、勾股定理等综合考查. 2.7 正方形探究问题二 正方形的判定 [解析] 本题先说明四边形是矩形,再求出有一组邻边相等即可,还可以先说明四边形是菱形,再求其一个内角为90°. 2.7 正方形[归纳总结] 正方形的判定方法多种多样,其基本思路是先判定一个四边形是矩形,再判定这个矩形也是菱形,或者先判定四边形是菱形,再判定这个菱形也是矩形,就可以判定这个四边形是正方形. 2.7 正方形探究问题三 平行四边形、菱形、矩形、正方形的综合 2∶12.7 正方形[解析] 对于(1),可直接运用SAS来判定两个三角形全等;对于(2),由于(1)中变相给出了BM=CM的提示,所以容易联想运用菱形的定义判断四边形MENF的形状;对于(3),相当于把(2)中的菱形变为正方形,那只需使∠BMC=90°了.此时∠AMB=∠DMC=45°,△ABM是等腰直角三角形,得AD=2AB. 2.7 正方形解:(1)证明:在矩形ABCD中,AB=CD,∠A=∠D=90°.
又∵M是AD的中点,∴AM=DM,
∴△ABM≌△DCM(SAS).
(2)四边形MENF是菱形.
证明:∵点E,F,N分别是BM,CM,CB的中点,
∴NF∥ME,NE∥MF,
∴四边形MENF是平行四边形.
由(1)得BM=CM,
∴ME=MF,∴?MENF是菱形.
(3)2∶1 2.7 正方形[归纳总结] 菱形、矩形、正方形都是特殊的平行四边形,它们之间的联系是:平行四边形有一组邻边相等时就变成菱形,菱形的一个角是直角时,该菱形就变成正方形.平行四边形有一个内角是直角时就变成矩形,矩形的一组邻边相等时就变成正方形.它们之间是紧密联系,不可分割的. 2.7 正方形
②菱形的四条边都______,菱形的对角线互相____________,且每条对角线平分一组对角.
③菱形的面积等于两条______________乘积的一半. 邻边 相等 垂直平分 对角线长度 2.7 正方形活动2 教材导学 是 是 是 2.7 正方形(2)与矩形比较,裁下的部分有四条边__________的特殊性质,与菱形比较,裁下的部分有四个角____________的特殊性质.
(3)结合小学学过的知识,你认为裁下的部分是________形. 都相等 都为直角 正方 ◆知识链接——[新知梳理]知识点三、四 2.7 正方形知识点一 正方形的定义 把一组____________且有一个角是________的平行四边形叫作正方形. 邻边相等 直角 2.7 正方形知识点二 正方形、菱形、矩形、平行四边形之间的关系 2.7 正方形知识点三 正方形的性质 1.四条边__________,四个角都是________;
2.对角线相等且互相____________,每条对角线平分一组对角;
3.是中心对称图形,对角线的交点是____________;
4.是轴对称图形,______________所在直线,以及过每一组对边中点的直线都是它的对称轴. 都相等 直角 垂直平分 对称中心 两条对角线 2.7 正方形知识点四 正方形的判定 在判定正方形时,通常先判定它是矩形或菱形,然后通过下列定理判定其为正方形:
1.有一组邻边相等的矩形是正方形;
2.对角线____________的矩形是正方形;
3.有一个角是直角的菱形是正方形;
4.对角线________的菱形是正方形. 互相垂直 相等 2.7 正方形探究问题一 正方形的性质 2.7 正方形2.7 正方形2.7 正方形解:(1)AD与CF还相等.
理由:∵四边形ODEF,四边形ABCO均为正方形,
∴∠DOF=∠COA=90°,DO=OF,CO=OA,
∴∠COF=∠AOD,
∴△COF≌△AOD(SAS),∴AD=CF. 2.7 正方形2.7 正方形[归纳总结] 正方形是特殊的菱形、矩形,所以正方形具有菱形、矩形的所有性质,理所当然地,正方形具有平行四边形的所有性质.正方形的性质常与全等三角形以及后面要学的相似三角形、勾股定理等综合考查. 2.7 正方形探究问题二 正方形的判定 [解析] 本题先说明四边形是矩形,再求出有一组邻边相等即可,还可以先说明四边形是菱形,再求其一个内角为90°. 2.7 正方形[归纳总结] 正方形的判定方法多种多样,其基本思路是先判定一个四边形是矩形,再判定这个矩形也是菱形,或者先判定四边形是菱形,再判定这个菱形也是矩形,就可以判定这个四边形是正方形. 2.7 正方形探究问题三 平行四边形、菱形、矩形、正方形的综合 2∶12.7 正方形[解析] 对于(1),可直接运用SAS来判定两个三角形全等;对于(2),由于(1)中变相给出了BM=CM的提示,所以容易联想运用菱形的定义判断四边形MENF的形状;对于(3),相当于把(2)中的菱形变为正方形,那只需使∠BMC=90°了.此时∠AMB=∠DMC=45°,△ABM是等腰直角三角形,得AD=2AB. 2.7 正方形解:(1)证明:在矩形ABCD中,AB=CD,∠A=∠D=90°.
又∵M是AD的中点,∴AM=DM,
∴△ABM≌△DCM(SAS).
(2)四边形MENF是菱形.
证明:∵点E,F,N分别是BM,CM,CB的中点,
∴NF∥ME,NE∥MF,
∴四边形MENF是平行四边形.
由(1)得BM=CM,
∴ME=MF,∴?MENF是菱形.
(3)2∶1 2.7 正方形[归纳总结] 菱形、矩形、正方形都是特殊的平行四边形,它们之间的联系是:平行四边形有一组邻边相等时就变成菱形,菱形的一个角是直角时,该菱形就变成正方形.平行四边形有一个内角是直角时就变成矩形,矩形的一组邻边相等时就变成正方形.它们之间是紧密联系,不可分割的. 2.7 正方形
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
