浙教版九年级下册 3.4 简单几何体的表面展开图 课件(共23张PPT)
文档属性
| 名称 | 浙教版九年级下册 3.4 简单几何体的表面展开图 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 518.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 15:30:09 | ||
图片预览


文档简介
(共23张PPT)
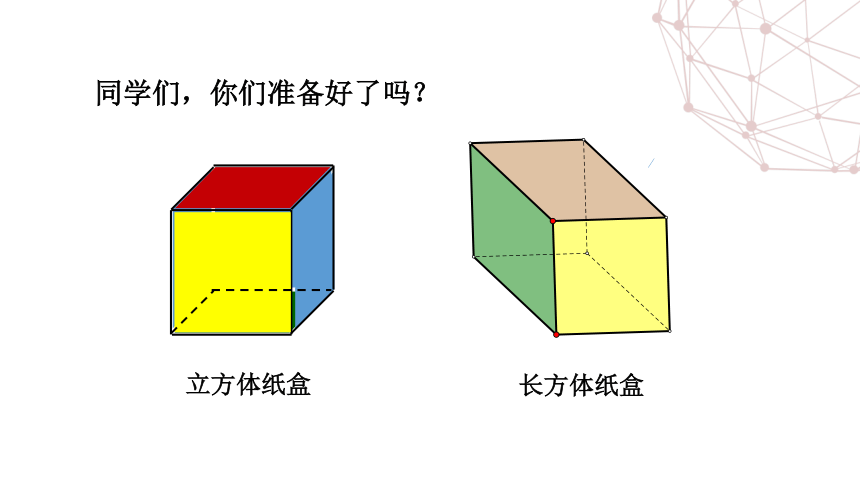
立方体纸盒
长方体纸盒
同学们,你们准备好了吗?
A
B
在一个长、宽、高分别为3米,2米,2米长方体房间内,一蜘蛛在点A处,一苍蝇在点B处.
(1)如图1,点A,B是长方体的顶点,试问蜘蛛为捉住B处的苍蝇,沿墙面的最近路线如何爬行?
图1
在一个长、宽、高分别为3米,2米,2米长方体房间内,一蜘蛛在点A处,一苍蝇在点B处.
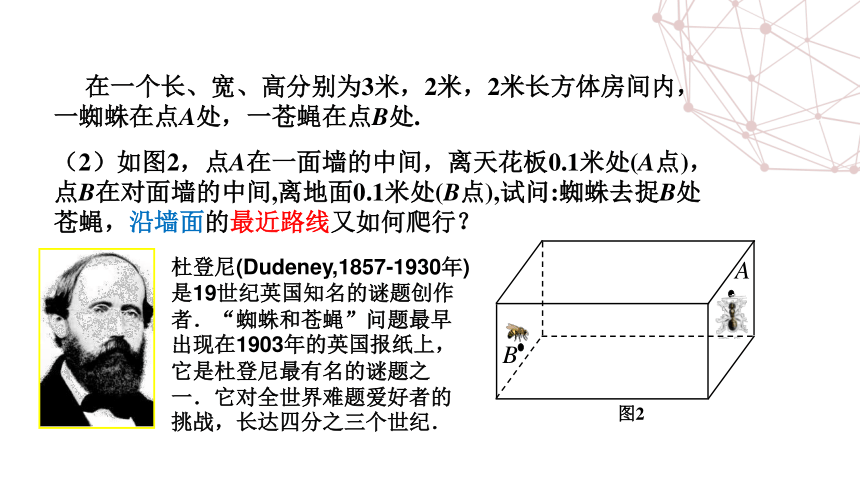
(2)如图2,点A在一面墙的中间,离天花板0.1米处(A点),点B在对面墙的中间,离地面0.1米处(B点),试问:蜘蛛去捉B处苍蝇,沿墙面的最近路线又如何爬行?
A
B
图2
杜登尼(Dudeney,1857-1930年)是19世纪英国知名的谜题创作者.“蜘蛛和苍蝇”问题最早出现在1903年的英国报纸上,它是杜登尼最有名的谜题之一.它对全世界难题爱好者的挑战,长达四分之三个世纪.
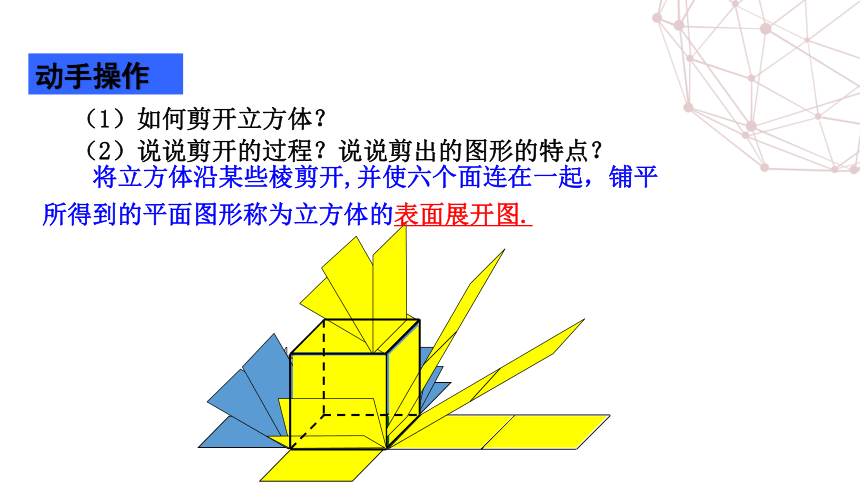
动手操作
(1)如何剪开立方体?
(2)说说剪开的过程?说说剪出的图形的特点?
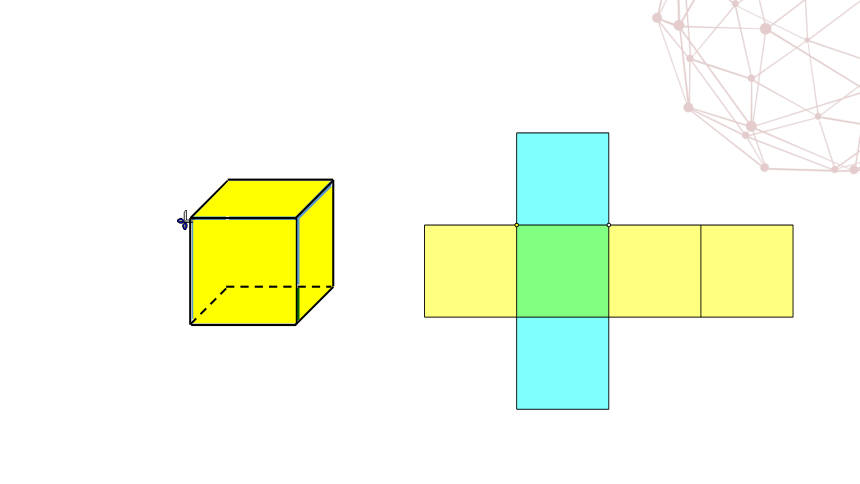
将立方体沿某些棱剪开,并使六个面连在一起,铺平所得到的平面图形称为立方体的表面展开图.
展开图
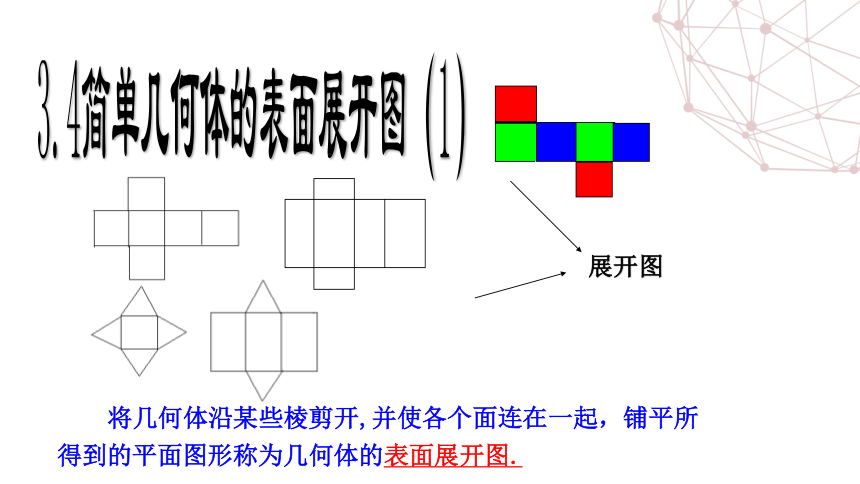
3.4简单几何体的表面展开图(1)
将几何体沿某些棱剪开,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图.
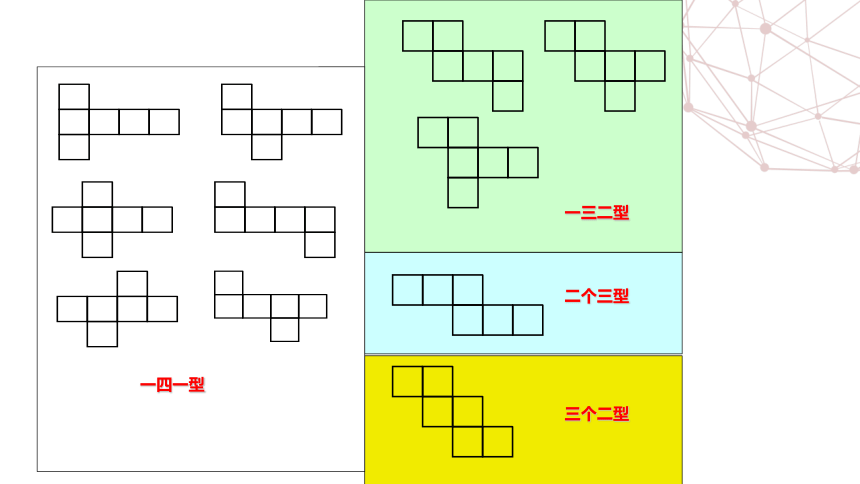
一四一型
一三二型
二个三型
三个二型
二个三型
归纳规律
一四一型
一三二型
三个二型
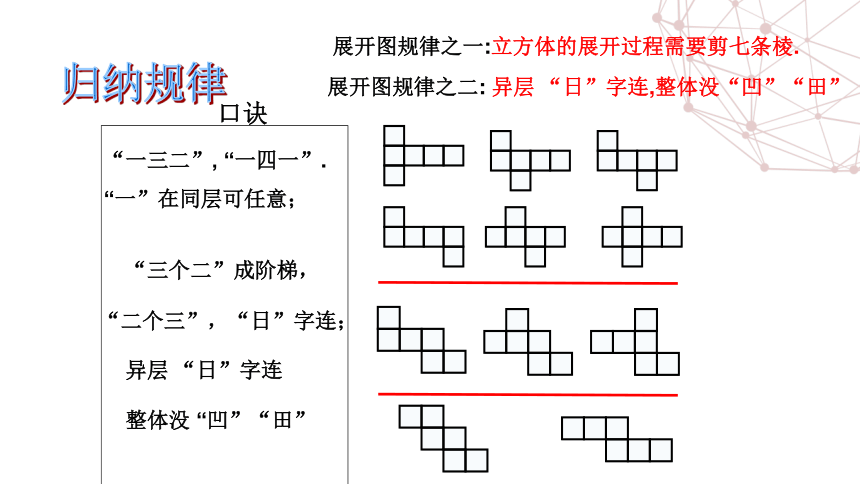
“一三二”, “一四一”.
“一”在同层可任意;
“三个二”成阶梯,
“二个三”,“日”字连;
异层 “日”字连
整体没 “凹”“田”
口诀
展开图规律之一:立方体的展开过程需要剪七条棱.
展开图规律之二: 异层 “日”字连,整体没“凹”“田”
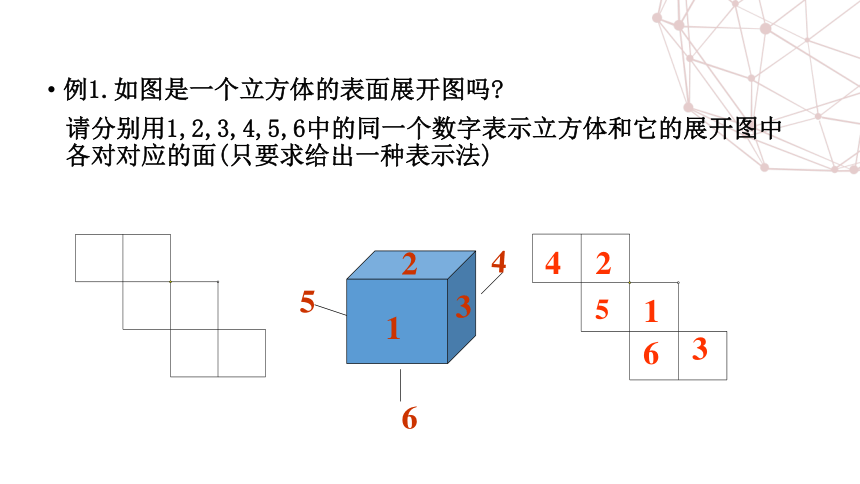
例1.如图是一个立方体的表面展开图吗
6
2
3
4
5
1
1
4
2
3
5
6
请分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示法)
a
变式:图是不是一个立方体的展开图?
将小正方形a添加到合适的位置,使它成为一个立方体的展开图,并说出与小正方形a相对的面.
(1)下图给出三种纸样,它们都正确吗?
例2:有一种牛奶软包装盒如图. 为了生产这种包装盒,需要先画出展开图纸样.
(1)解:图中,因为表示底面的两个长方形不可能在同一侧,所以图乙不正确. 图甲和图丙都正确.
甲 乙 丙
(2)从已知正确的纸样中选出一种,标注上尺寸;
(2)解:若选图甲,可得表面展开图及尺寸标注如下图所示.
甲 乙 丙
1
5
4
6
3
2
a
a
h
b
b
b
b
a
1
5
6
3
2
4
甲
(3)解:由右图得,包装盒的侧面积为
(3)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和).
甲 乙 丙
1
5
4
6
3
2
a
a
h
b
b
b
b
a
1
5
6
3
2
4
甲
挑战世纪谜题
---- “蜘蛛和苍蝇”问题
在一个长、宽、高分别为3米,2米,2米长方体房间内,一蜘蛛在点A处,一苍蝇在点B处.
(2)如图2,点A在一面墙的中间,离天花板0.1米处(A点),点B在对面墙的中间,离地面0.1米处(B点),试问:蜘蛛去捉B处苍蝇,沿墙面的最近路线又如何爬行?
A
B
图2
杜登尼(Dudeney,1857-1930年)是19世纪英国知名的谜题创作者.“蜘蛛和苍蝇”问题最早出现在1903年的英国报纸上,它是杜登尼最有名的谜题之一.它对全世界难题爱好者的挑战,长达四分之三个世纪.
A.
B.
A.
.B
A.
B.
AB=5
AB=5
C
A
B
A
C
B
C”(C)
C’(C)
4cm
如图,有一边长4米立方体形的房间,一只蜘蛛在A处,一只苍蝇在B处。⑴试问,蜘蛛去抓苍蝇需要爬行的最短路程是多少?
4cm
⑵若苍蝇在C处,则最短路程是多少?
二个三型
归纳规律
一四一型
一三二型
三个二型
“一三二”, “一四一”.
“一”在同层可任意;
“三个二”成阶梯,
“二个三”,“日”字连;
异层 “日”字连
整体没 “凹”“田”
口诀
展开图规律之一:立方体的展开过程需要剪七条棱.
展开图规律之二: 异层 “日”字连,整体没“凹”“田”
作业1:九下作业本(2)3.4(1).
作业2:PPT剩下内容的学习.
作业建议
√
×
×
√
×
√
1、下列平面图形能折叠成正方体吗?
2、下面哪些图形经过折叠可以围成一个棱柱?
(1) (2)
(3) (4) (5)
3、添上一个小正方形,使下图折叠后能围成一个立方体,共有几种添法?
c
7
-1
b
a
4、如图是一个正方体纸盒的展开图,图中的6个正方形中分别已填入了-1、7、 、a、b、c,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:
5、 有一个正方体,在它的各个面上分别写了①、②、③、④、⑤、⑥。甲、乙、丙三位同学从三个不同的角度去观察此正方体,结果如下图,问这个正方体各个面的对面的是什么数?
⑥
②
④
甲
②
③
①
乙
④
③
⑤
丙
立方体纸盒
长方体纸盒
同学们,你们准备好了吗?
A
B
在一个长、宽、高分别为3米,2米,2米长方体房间内,一蜘蛛在点A处,一苍蝇在点B处.
(1)如图1,点A,B是长方体的顶点,试问蜘蛛为捉住B处的苍蝇,沿墙面的最近路线如何爬行?
图1
在一个长、宽、高分别为3米,2米,2米长方体房间内,一蜘蛛在点A处,一苍蝇在点B处.
(2)如图2,点A在一面墙的中间,离天花板0.1米处(A点),点B在对面墙的中间,离地面0.1米处(B点),试问:蜘蛛去捉B处苍蝇,沿墙面的最近路线又如何爬行?
A
B
图2
杜登尼(Dudeney,1857-1930年)是19世纪英国知名的谜题创作者.“蜘蛛和苍蝇”问题最早出现在1903年的英国报纸上,它是杜登尼最有名的谜题之一.它对全世界难题爱好者的挑战,长达四分之三个世纪.
动手操作
(1)如何剪开立方体?
(2)说说剪开的过程?说说剪出的图形的特点?
将立方体沿某些棱剪开,并使六个面连在一起,铺平所得到的平面图形称为立方体的表面展开图.
展开图
3.4简单几何体的表面展开图(1)
将几何体沿某些棱剪开,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图.
一四一型
一三二型
二个三型
三个二型
二个三型
归纳规律
一四一型
一三二型
三个二型
“一三二”, “一四一”.
“一”在同层可任意;
“三个二”成阶梯,
“二个三”,“日”字连;
异层 “日”字连
整体没 “凹”“田”
口诀
展开图规律之一:立方体的展开过程需要剪七条棱.
展开图规律之二: 异层 “日”字连,整体没“凹”“田”
例1.如图是一个立方体的表面展开图吗
6
2
3
4
5
1
1
4
2
3
5
6
请分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示法)
a
变式:图是不是一个立方体的展开图?
将小正方形a添加到合适的位置,使它成为一个立方体的展开图,并说出与小正方形a相对的面.
(1)下图给出三种纸样,它们都正确吗?
例2:有一种牛奶软包装盒如图. 为了生产这种包装盒,需要先画出展开图纸样.
(1)解:图中,因为表示底面的两个长方形不可能在同一侧,所以图乙不正确. 图甲和图丙都正确.
甲 乙 丙
(2)从已知正确的纸样中选出一种,标注上尺寸;
(2)解:若选图甲,可得表面展开图及尺寸标注如下图所示.
甲 乙 丙
1
5
4
6
3
2
a
a
h
b
b
b
b
a
1
5
6
3
2
4
甲
(3)解:由右图得,包装盒的侧面积为
(3)利用你所选的一种纸样,求出包装盒的侧面积和表面积(侧面积与两个底面积的和).
甲 乙 丙
1
5
4
6
3
2
a
a
h
b
b
b
b
a
1
5
6
3
2
4
甲
挑战世纪谜题
---- “蜘蛛和苍蝇”问题
在一个长、宽、高分别为3米,2米,2米长方体房间内,一蜘蛛在点A处,一苍蝇在点B处.
(2)如图2,点A在一面墙的中间,离天花板0.1米处(A点),点B在对面墙的中间,离地面0.1米处(B点),试问:蜘蛛去捉B处苍蝇,沿墙面的最近路线又如何爬行?
A
B
图2
杜登尼(Dudeney,1857-1930年)是19世纪英国知名的谜题创作者.“蜘蛛和苍蝇”问题最早出现在1903年的英国报纸上,它是杜登尼最有名的谜题之一.它对全世界难题爱好者的挑战,长达四分之三个世纪.
A.
B.
A.
.B
A.
B.
AB=5
AB=5
C
A
B
A
C
B
C”(C)
C’(C)
4cm
如图,有一边长4米立方体形的房间,一只蜘蛛在A处,一只苍蝇在B处。⑴试问,蜘蛛去抓苍蝇需要爬行的最短路程是多少?
4cm
⑵若苍蝇在C处,则最短路程是多少?
二个三型
归纳规律
一四一型
一三二型
三个二型
“一三二”, “一四一”.
“一”在同层可任意;
“三个二”成阶梯,
“二个三”,“日”字连;
异层 “日”字连
整体没 “凹”“田”
口诀
展开图规律之一:立方体的展开过程需要剪七条棱.
展开图规律之二: 异层 “日”字连,整体没“凹”“田”
作业1:九下作业本(2)3.4(1).
作业2:PPT剩下内容的学习.
作业建议
√
×
×
√
×
√
1、下列平面图形能折叠成正方体吗?
2、下面哪些图形经过折叠可以围成一个棱柱?
(1) (2)
(3) (4) (5)
3、添上一个小正方形,使下图折叠后能围成一个立方体,共有几种添法?
c
7
-1
b
a
4、如图是一个正方体纸盒的展开图,图中的6个正方形中分别已填入了-1、7、 、a、b、c,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:
5、 有一个正方体,在它的各个面上分别写了①、②、③、④、⑤、⑥。甲、乙、丙三位同学从三个不同的角度去观察此正方体,结果如下图,问这个正方体各个面的对面的是什么数?
⑥
②
④
甲
②
③
①
乙
④
③
⑤
丙
