浙教版九年级下册 1.1 锐角三角函数 课件(共28张PPT)
文档属性
| 名称 | 浙教版九年级下册 1.1 锐角三角函数 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-08 15:45:52 | ||
图片预览


文档简介
(共28张PPT)
第一章 解直角三角形
1.1锐角三角函数(1)
动手实验
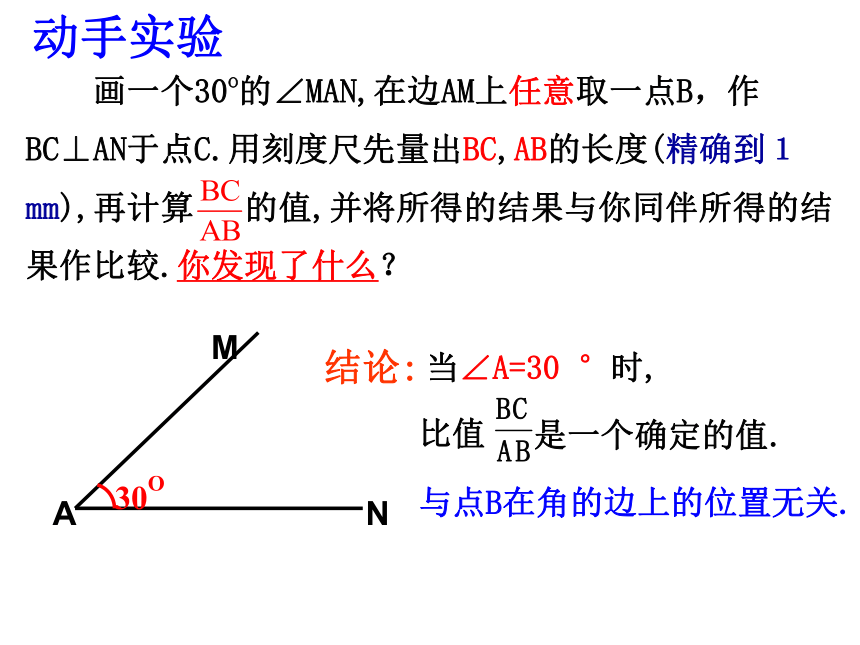
画一个30o的∠MAN,在边AM上任意取一点B,作BC⊥AN于点C.用刻度尺先量出BC,AB的长度(精确到1mm),再计算 的值,并将所得的结果与你同伴所得的结果作比较.你发现了什么?
A
M
N
30O
与点B在角的边上的位置无关.
当∠A=30 °时,
比值
是一个确定的值.
猜想:
结论:
动手实验
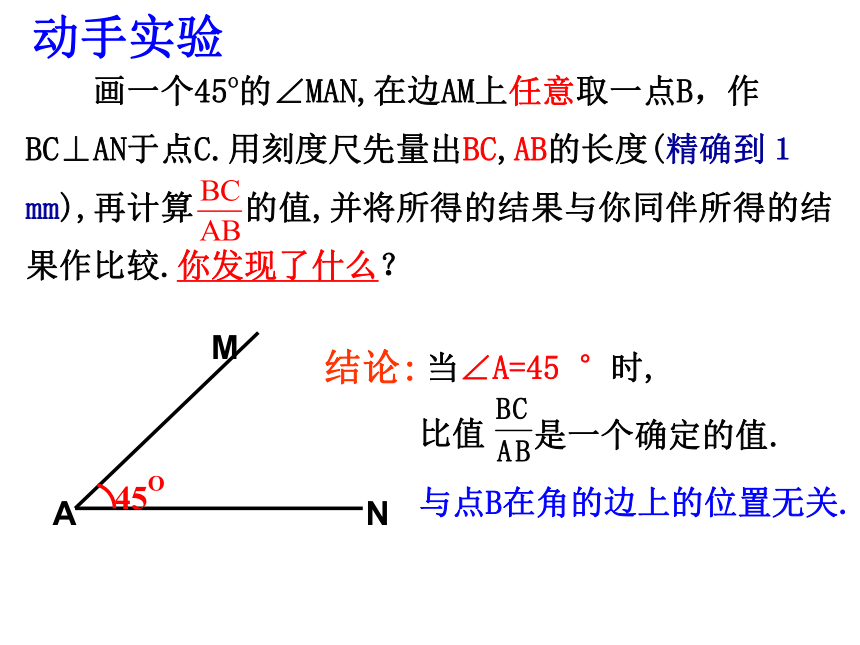
画一个45o的∠MAN,在边AM上任意取一点B,作BC⊥AN于点C.用刻度尺先量出BC,AB的长度(精确到1mm),再计算 的值,并将所得的结果与你同伴所得的结果作比较.你发现了什么?
A
M
N
45O
与点B在角的边上的位置无关.
当∠A=45 °时,
比值
是一个确定的值.
猜想:
结论:
发现规律
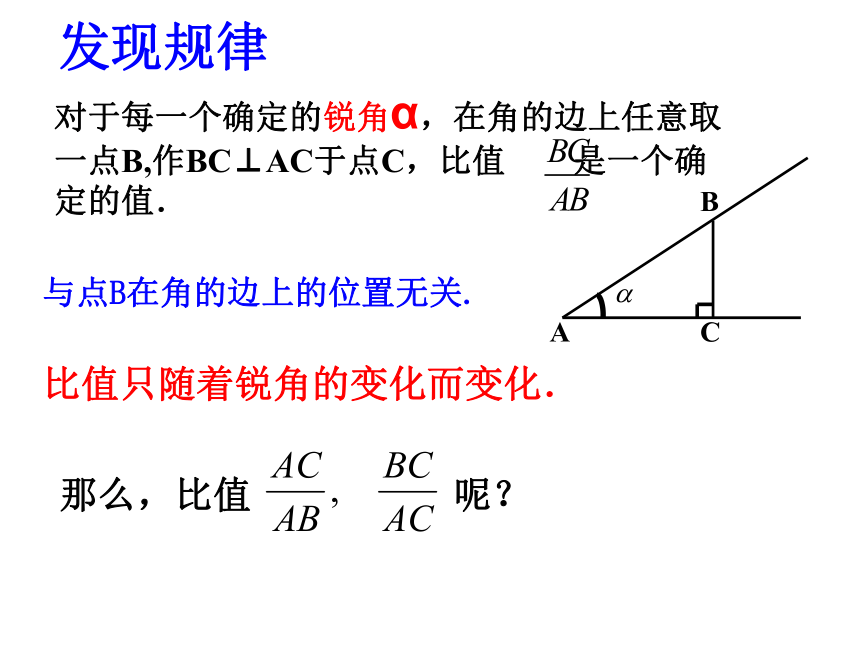
对于每一个确定的锐角α,在角的边上任意取一点B,作BC⊥AC于点C,比值 是一个确定的值.
A
B
C
比值只随着锐角的变化而变化.
与点B在角的边上的位置无关.
那么,比值 呢?
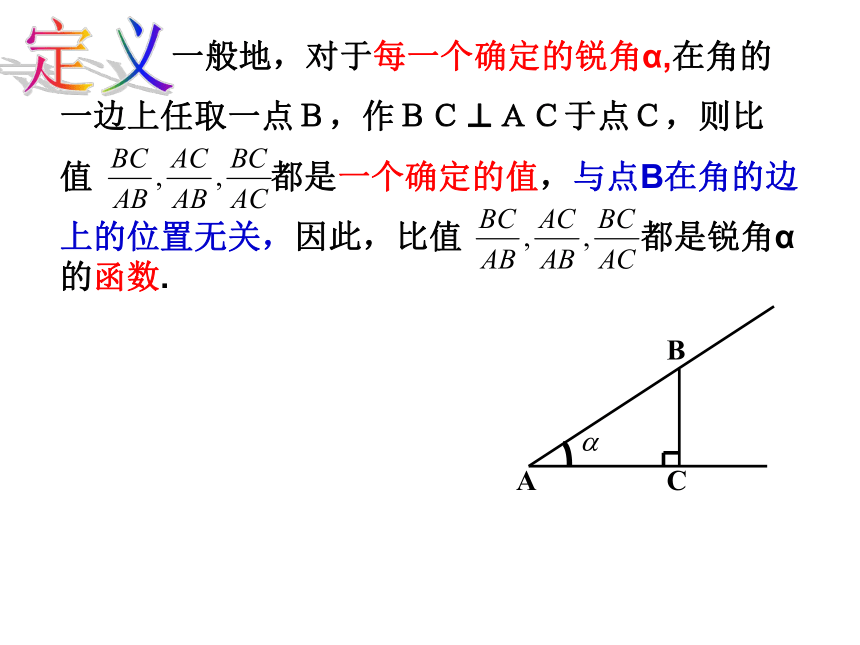
一般地,对于每一个确定的锐角α,在角的
一边上任取一点B,作BC⊥AC于点C,则比
值 都是一个确定的值,与点B在角的边
上的位置无关,因此,比值 都是锐角α的函数.
A
B
C
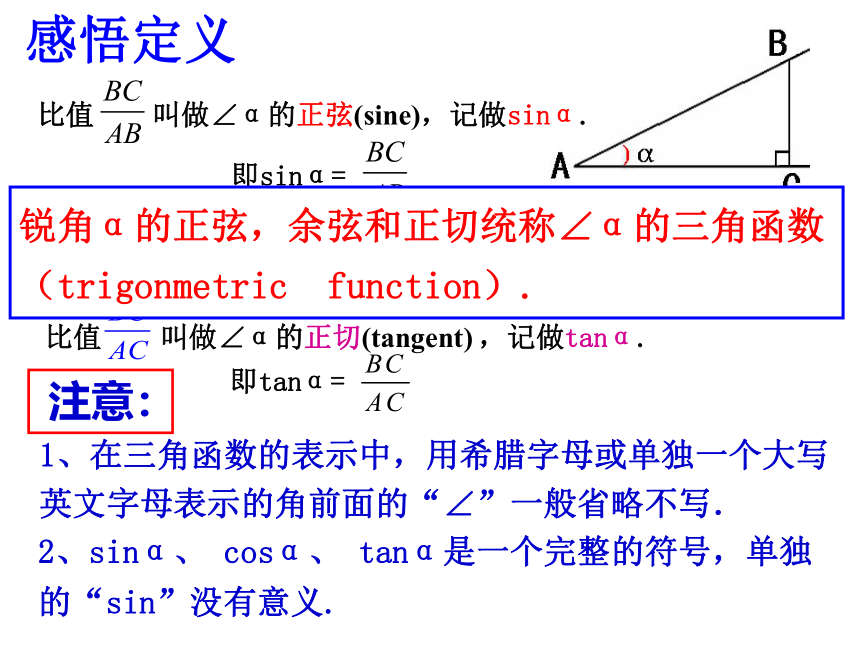
比值 叫做∠α的正弦(sine),记做sinα.
比值 叫做∠α的余弦(cosine) ,记做cosα.
即cosα=
比值 叫做∠α的正切(tangent) ,记做tanα.
即tanα=
感悟定义
即sinα=
注意:
1、在三角函数的表示中,用希腊字母或单独一个大写英文字母表示的角前面的“∠”一般省略不写.
2、sinα、 cosα、 tanα是一个完整的符号,单独的“sin”没有意义.
锐角α的正弦,余弦和正切统称∠α的三角函数(trigonmetric function).
三角函数的由来
“三角学”一词,是由希腊文三角形与测量二字构成的,原意是三角形的测量,也就是解三角形.后来范围逐渐扩大,成为研究三角函数及其应用的一个数学分支.
三角测量在我国出现的很早.据记载,早在公元前两千年,大禹就利用三角形的边角关系,来进行对山川地势的测量.
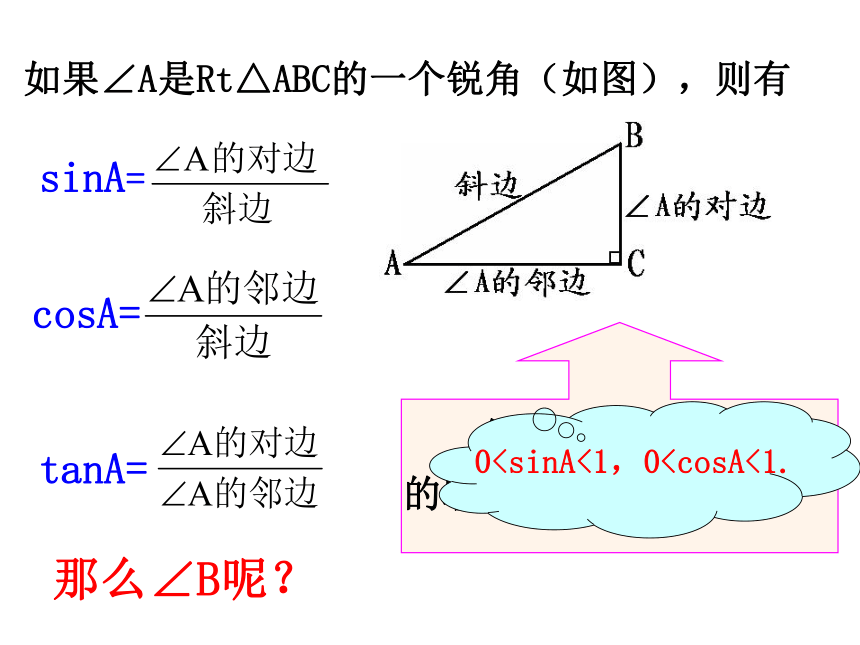
如果∠A是Rt△ABC的一个锐角(如图),则有
sinA=
cosA=
tanA=
你能求出sinA与cosA的取值范围吗?
0那么∠B呢?
已知直角三角形中的两边或两边之比,就能求出锐角三角函数值.
解后语:
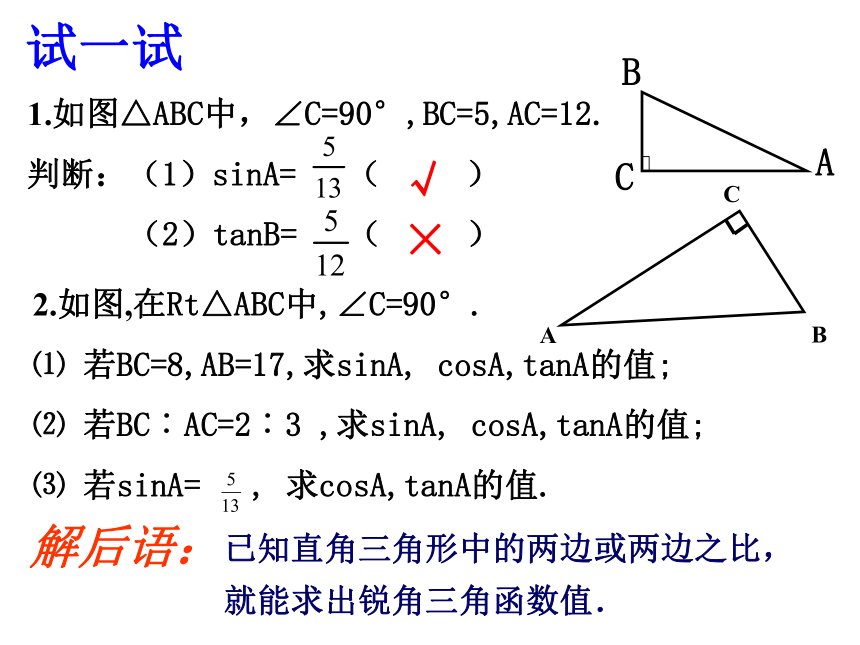
1.如图△ABC中,∠C=90°,BC=5,AC=12.
判断:(1)sinA= ( )
(2)tanB= ( )
A
B
C
2.如图,在Rt△ABC中,∠C=90°.
⑴ 若BC=8,AB=17,求sinA, cosA,tanA的值;
⑵ 若BC︰AC=2︰3 ,求sinA, cosA,tanA的值;
⑶ 若sinA= , 求cosA,tanA的值.
A
B
C
√
×
试一试
3、如图,在Rt△ABC中,∠C=Rt∠,若AB=5,BC=3.
(2)请求出∠B的正弦、余弦和正切的值.
(1)求∠A的正弦、余弦和正切的值;
C
A
B
5
3
(3)观察(1)(2)中的计算结果,你发现了什么
当∠A+∠B=90°时,
sinA=cosB,
cosA=sinB,
tanA·tanB=1.
试一试
4、如图,在△ABC中,若AB=5,BC=3,则下列结论正确的是( )
A.sinA=
B.sinA=
C.sinA=
D.以上结论都不正确
C
A
B
3
5
D
5、如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于D,
若BD=2,BC=3.则sinA= .
3
D
B
C
A
2
7.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
8.已知∠A,∠B为锐角.
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.
A
B
C
┌
C
=
=
提示:过点A作AD垂直于BC于D.
5
5
6
A
B
C
┌
D
练一练
1.如图:在等腰△ABC中,AB=AC=5,BC=6.
求sinB,cosB,tanB.
2. 在Rt△ABC中,∠C为Rt∠ .
求证:sin2A+cos2A=1.
A
B
C
┌
证明:∵∠C=Rt∠
AC2+BC2=AB2
∴sinA= ,cosA=
经历了一个探究过程:特殊到一般
学习了一个重要概念:锐角三角函数
∠α的正弦
∠α的余弦
∠α的正切
在本节课中,我们……
体现了一种数学思想:数形结合
你说
我说
在本节课中,我们……
你说
我说
还要注意:
若锐角所在三角形不是直角三角形时,
应设法构造一个以该锐角为内角的直角三角形,再求锐角三角函数值
5
4
0
x
y
1
6
3
2
4
3
B
5
2
1
1、在平面坐标系第一象限内是否存在点P,使得OP=4, sin∠POB=0.5.求点P的坐标,并求出OP所在直线的解析式.
思考:OP所在直线的解析式的比例系数K与∠POB有什么关系呢
拓展探索:
拓展探索:
2、如图,一根3m长的竹竿AB斜靠在墙上,当端点A离地面的高度AC长为1m时,竹竿AB的倾斜角α的正切tanα的值是多少?
当端点A位于D,离地面的高度CD为2m时,倾斜角β的正切tanβ的值是多少?
tanα的值可以大于100吗?请求出锐角α的正切函数的范围。
E
D
A
C
B
α
β
谈谈今天的收获
问题:甲、乙两队分别在通向江郎山主峰顶倾斜角为30°
和40°的斜坡上都步行了600米,那么乙队比甲队高多少米?
现在你会了吗
30°
600米
甲队
40°
乙队
600米
40°
600米
A
C
B
300米
200
A
C
B
┌
例1、如图:在Rt△ABC中,∠B=900, AC=200, sinA=0.6.求BC的长.
解:∵ ∠B=900
∴ sinA= =0.6
∴BC=0.6AC=120
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
斜边
回味无穷
定义中应该注意的几个问题:
1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A
的三角函数,习惯省去“∠”号;
3.sinA,cosA,tanA, 是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
下课了!
第一章 解直角三角形
1.1锐角三角函数(1)
动手实验
画一个30o的∠MAN,在边AM上任意取一点B,作BC⊥AN于点C.用刻度尺先量出BC,AB的长度(精确到1mm),再计算 的值,并将所得的结果与你同伴所得的结果作比较.你发现了什么?
A
M
N
30O
与点B在角的边上的位置无关.
当∠A=30 °时,
比值
是一个确定的值.
猜想:
结论:
动手实验
画一个45o的∠MAN,在边AM上任意取一点B,作BC⊥AN于点C.用刻度尺先量出BC,AB的长度(精确到1mm),再计算 的值,并将所得的结果与你同伴所得的结果作比较.你发现了什么?
A
M
N
45O
与点B在角的边上的位置无关.
当∠A=45 °时,
比值
是一个确定的值.
猜想:
结论:
发现规律
对于每一个确定的锐角α,在角的边上任意取一点B,作BC⊥AC于点C,比值 是一个确定的值.
A
B
C
比值只随着锐角的变化而变化.
与点B在角的边上的位置无关.
那么,比值 呢?
一般地,对于每一个确定的锐角α,在角的
一边上任取一点B,作BC⊥AC于点C,则比
值 都是一个确定的值,与点B在角的边
上的位置无关,因此,比值 都是锐角α的函数.
A
B
C
比值 叫做∠α的正弦(sine),记做sinα.
比值 叫做∠α的余弦(cosine) ,记做cosα.
即cosα=
比值 叫做∠α的正切(tangent) ,记做tanα.
即tanα=
感悟定义
即sinα=
注意:
1、在三角函数的表示中,用希腊字母或单独一个大写英文字母表示的角前面的“∠”一般省略不写.
2、sinα、 cosα、 tanα是一个完整的符号,单独的“sin”没有意义.
锐角α的正弦,余弦和正切统称∠α的三角函数(trigonmetric function).
三角函数的由来
“三角学”一词,是由希腊文三角形与测量二字构成的,原意是三角形的测量,也就是解三角形.后来范围逐渐扩大,成为研究三角函数及其应用的一个数学分支.
三角测量在我国出现的很早.据记载,早在公元前两千年,大禹就利用三角形的边角关系,来进行对山川地势的测量.
如果∠A是Rt△ABC的一个锐角(如图),则有
sinA=
cosA=
tanA=
你能求出sinA与cosA的取值范围吗?
0
已知直角三角形中的两边或两边之比,就能求出锐角三角函数值.
解后语:
1.如图△ABC中,∠C=90°,BC=5,AC=12.
判断:(1)sinA= ( )
(2)tanB= ( )
A
B
C
2.如图,在Rt△ABC中,∠C=90°.
⑴ 若BC=8,AB=17,求sinA, cosA,tanA的值;
⑵ 若BC︰AC=2︰3 ,求sinA, cosA,tanA的值;
⑶ 若sinA= , 求cosA,tanA的值.
A
B
C
√
×
试一试
3、如图,在Rt△ABC中,∠C=Rt∠,若AB=5,BC=3.
(2)请求出∠B的正弦、余弦和正切的值.
(1)求∠A的正弦、余弦和正切的值;
C
A
B
5
3
(3)观察(1)(2)中的计算结果,你发现了什么
当∠A+∠B=90°时,
sinA=cosB,
cosA=sinB,
tanA·tanB=1.
试一试
4、如图,在△ABC中,若AB=5,BC=3,则下列结论正确的是( )
A.sinA=
B.sinA=
C.sinA=
D.以上结论都不正确
C
A
B
3
5
D
5、如图,在Rt△ABC中,∠ACB=90°,作CD⊥AB于D,
若BD=2,BC=3.则sinA= .
3
D
B
C
A
2
7.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
8.已知∠A,∠B为锐角.
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.
A
B
C
┌
C
=
=
提示:过点A作AD垂直于BC于D.
5
5
6
A
B
C
┌
D
练一练
1.如图:在等腰△ABC中,AB=AC=5,BC=6.
求sinB,cosB,tanB.
2. 在Rt△ABC中,∠C为Rt∠ .
求证:sin2A+cos2A=1.
A
B
C
┌
证明:∵∠C=Rt∠
AC2+BC2=AB2
∴sinA= ,cosA=
经历了一个探究过程:特殊到一般
学习了一个重要概念:锐角三角函数
∠α的正弦
∠α的余弦
∠α的正切
在本节课中,我们……
体现了一种数学思想:数形结合
你说
我说
在本节课中,我们……
你说
我说
还要注意:
若锐角所在三角形不是直角三角形时,
应设法构造一个以该锐角为内角的直角三角形,再求锐角三角函数值
5
4
0
x
y
1
6
3
2
4
3
B
5
2
1
1、在平面坐标系第一象限内是否存在点P,使得OP=4, sin∠POB=0.5.求点P的坐标,并求出OP所在直线的解析式.
思考:OP所在直线的解析式的比例系数K与∠POB有什么关系呢
拓展探索:
拓展探索:
2、如图,一根3m长的竹竿AB斜靠在墙上,当端点A离地面的高度AC长为1m时,竹竿AB的倾斜角α的正切tanα的值是多少?
当端点A位于D,离地面的高度CD为2m时,倾斜角β的正切tanβ的值是多少?
tanα的值可以大于100吗?请求出锐角α的正切函数的范围。
E
D
A
C
B
α
β
谈谈今天的收获
问题:甲、乙两队分别在通向江郎山主峰顶倾斜角为30°
和40°的斜坡上都步行了600米,那么乙队比甲队高多少米?
现在你会了吗
30°
600米
甲队
40°
乙队
600米
40°
600米
A
C
B
300米
200
A
C
B
┌
例1、如图:在Rt△ABC中,∠B=900, AC=200, sinA=0.6.求BC的长.
解:∵ ∠B=900
∴ sinA= =0.6
∴BC=0.6AC=120
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
cosA
∠A的邻边
∠A的对边
斜边
sinA
斜边
斜边
回味无穷
定义中应该注意的几个问题:
1.sinA,cosA,tanA, 是在直角三角形中定义的, ∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA, 是一个完整的符号,表示∠A
的三角函数,习惯省去“∠”号;
3.sinA,cosA,tanA, 是一个比值.注意比的顺序,
且sinA,cosA,tanA, 均﹥0,无单位.
4.sinA,cosA,tanA, 的大小只与∠A的大小有关,
而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
下课了!
