浙教版数学八年级上册1.5 三角形全等的判定 同步测试(培优版)(含解析)
文档属性
| 名称 | 浙教版数学八年级上册1.5 三角形全等的判定 同步测试(培优版)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-07 20:32:14 | ||
图片预览




文档简介
浙教版数学八年级上册1.5 三角形全等的判定 同步测试
班级: 姓名:
同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你收获满满,学习进步,榜上有名!
一、选择题
1.如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
A. 两点之间 B. 两点之间
C. 两点之间 D. 两点之间
2.阅读以下作图步骤:
①在和上分别截取,使;②分别以为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线,连接,如图所示.根据以上作图,一定可以推得的结论是( )
A.且 B.且
C.且 D.且
3.如图,中,,,三条角平分线、、交于,于下列结论:;;平分;其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.4个
4.如图,点E是△ABC内一点,∠AEB=90°,AE平分∠BAC,D是边AB的中点,延长线段DE交边BC于点F,若AB=6,EF=1,则线段AC的长为( )
A.7 B. C.8 D.9
5.如图,中,分别是其角平分线和中线,过点C作于F,连接,则线段的长为( )
A. B.2 C. D.3
6.如图,的角平分线,交于点,,的面积为16,四边形的面积为5,则的面积为( )
A.5 B.5.5 C.6 D.7
7.对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接,,过点A作直线n与直线垂直,设是,直线n与所夹的锐角是,求x与y的数量关系.”下面是三个同学的答案,甲:,乙:,丙:.
对于三人的答案,下列结论正确的是( )
A.只有甲的答案正确 B.甲和乙的答案合在一起才正确
C.甲和丙的答案合在一起才正确 D.甲乙丙的答案合在一起才正确
8.如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
9.给定三角形的两个元素,画出的三角形的形状和大小都是不能确定的,在下列给定的条件下,再增加一个“”的条件后,所画出的三角形形状和大小仍不能完全确定的是( )
A., B.,
C., D.,
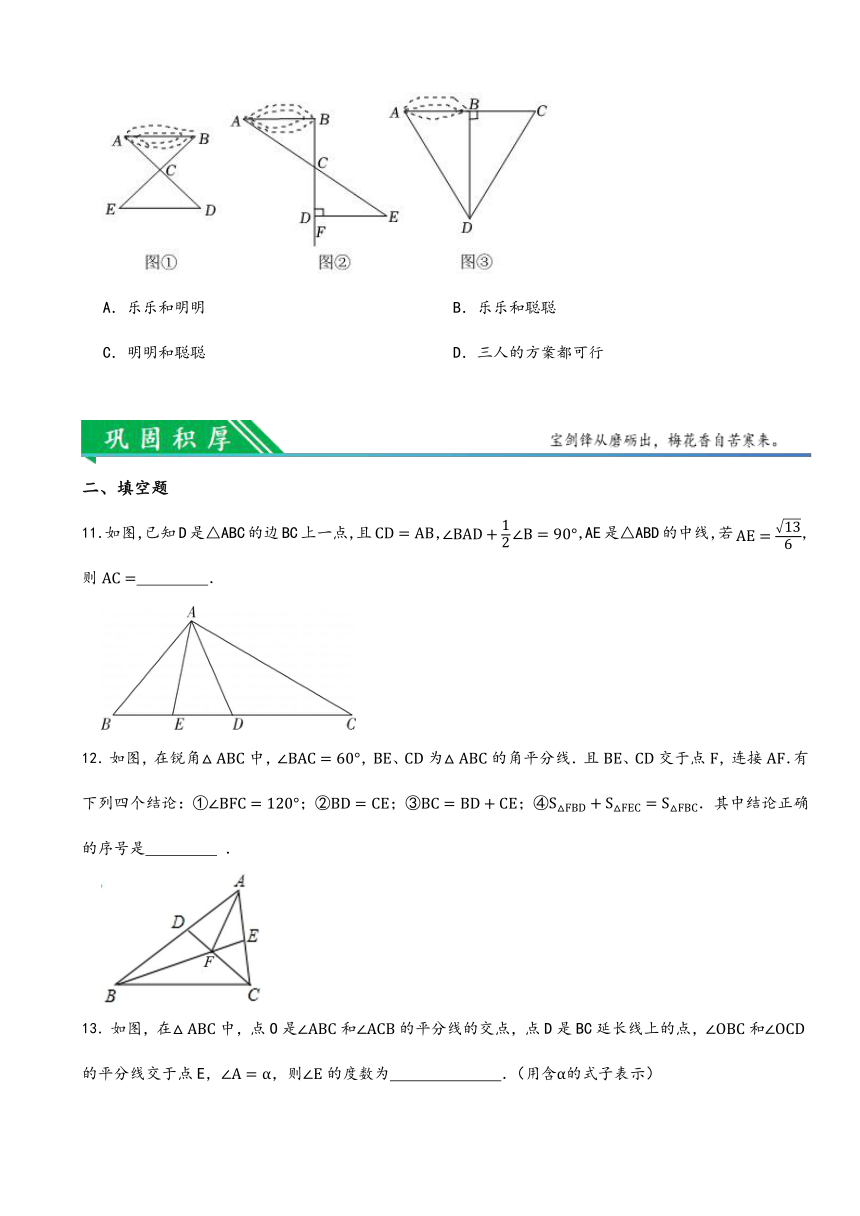
10.乐乐所在的七年级某班学生到野外活动,为测量池塘两端,的距离,乐乐、明明、聪聪三位同学分别设计出如下几种方案:
乐乐:如图,先在平地取一个可直接到达,的点,再连接,,并分别延长至,至,使,,最后测出的长即为,的距离.
明明:如图,先过点作的垂线,再在上取,两点,使,接着过点作的垂线,交的延长线于点,则测出的长即为,的距离.
聪聪:如图,过点作,再由点观测,在的延长线上取一点,使这时只要测出的长即为,的距离.
以上三位同学所设计的方案中可行的是( )
A.乐乐和明明 B.乐乐和聪聪
C.明明和聪聪 D.三人的方案都可行
二、填空题
11.如图,已知D是△ABC的边BC上一点,且,,AE是△ABD的中线,若,则 .
12.如图,在锐角中,,、为的角平分线.且、交于点,连接.有下列四个结论:①;②;③;④.其中结论正确的序号是 .
13.如图,在中,点O是和的平分线的交点,点D是BC延长线上的点,和的平分线交于点E,,则的度数为 .(用含的式子表示)
14.如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若,则 度.
15.在△ABC中,∠ABC=62°,∠ACB=50°,∠ACD是△ABC的外角 ∠ACD和∠ABC的平分线交于点E,则∠AEB=
16.如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .
三、解答题
17.
(1)如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹.
(2)如图a,在△ABC中, ∠ACB= 90°,∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
(3)如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.
要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?
19.已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图3.写出AF、EF与AB的数量关系,并对图②进行证明.
20.如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
21.如图(1),,,垂足分别为、,点在线段上以的速度由点向点运动,同时点在射线上运动.它们运动的时间为当点运动结束时,点运动随之结束.
(1)AP , 用含的代数式表示;
(2)若点的运动速度与点的运动速度相等,当时,与是否全等,并判断此时线段和线段的位置关系,请分别说明理由;
(3)如图(2),若“,”改为“”,点的运动速度为,其它条件不变,当点、运动到何处时有与全等,求出相应的的值.
22.已知,点为平面内一点,于.
(1)如图1,直接写出和之间的数量关系 ;
(2)如图2,过点作于点,求证:;
(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分,平分,若,,直接写出的度数.
23.综合与实践
(1)问题探究:如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在和上分别取点C和D,使得,连接,以为边作等边三角形,则就是的平分线.
请写出平分的依据: ;
(2)类比迁移:
小明根据以上信息研究发现:不一定必须是等边三角形,只需即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在的边,上分别取,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线是的平分线,请说明此做法的理由;
(3)拓展实践:
小明将研究应用于实践.如图4,校园的两条小路和,汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
24.下面是张老师数学课堂教学实践活动的一个片段:
【问题背景】如图1,一副三角板的直角顶点重合,两条直角边分别共线,将它们分别记作,.其中,,,.现固定三角板,将三角板绕点A逆时针旋转,旋转角记为,射线与射线交于点P,在射线上取一点Q,使,连接CQ.
(1)【特例探究】如图2,当时,直接写出和的数量关系和位置关系.
(2)【归纳证明】如图3,当点P在线段BC上时,【特例探究】中得到的结论是否成立,若成立,请给出证明;若不成立,请说明理由.
(3)【类比迁移】当点P在线段延长线上时,请直接写出【特例探究】中结论是否成立,不必说明理由.
(4)【拓展应用】连接.若,的面积等于,请直接写出的长.
1.【答案】D
【解析】【解答】解:A.若钉在E,H两点之间构成了三角形,能固定窗框,故不符合题意;
B.若钉在A,C两点之间能构成三角形,能固定窗框,故不符合题意;
C.若钉在F,E两点之间能构成三角形,能固定窗框,故不符合题意;
D.若钉在E,G两点之间不能构成三角形,不能固定窗框,故符合题意;
故答案为:D.
【分析】利用三角形的定义判断求解即可。
2.【答案】A
【解析】【解答】解:由作图可得:CM=DM.
∵CM=DM,OC=OD,OM=OM,
∴△OCM≌△ODM(SSS),
∴∠1=∠2.
故答案为:A.
【分析】由作图可得:CM=DM,OC=OD,利用SSS证明△OCM≌△ODM,据此判断.
3.【答案】C
【解析】【解答】解: ,
,
,
, ,
,
故①正确;
于H ,
,
,
,
,
,
,
故②正确;
, ,
,
,
,
, ,
,
,
,
,
故③错误;
如图,在BC上截取BI=BF,连接OI ,
,
,
,
,
在△OBI和△OBF中,
,
∴△OBI≌△OBF(SAS)
,
,
,
,
在△CIO与△CEO中,
,
∴△CIO≌△CEO(ASA)
,
,
故④正确.
故答案为:C.
【分析】易得∠ABC+∠ACB=120°,由角平分线的概念可得∠OBC=∠ABC,∠OCB=∠ACB,则∠OBC+∠OCB=60°,利用内角和定理求出∠BOC的度数,据此判断①;根据余角的性质结合外角的性质可得∠DOH=90°-∠BAD-∠ABC,结合角平分线的概念以及内角和定理可得∠DOH=(∠ACB-∠ABC),进而判断②;易得∠ACB>60°,则∠ABC4.【答案】C
【解析】【解答】解:延长BE交AC于H,
∵AE平分∠BAC,
∴∠HAE=∠BAE,
∵∠AEB=90°,
∴∠AEB=∠AEH=90°,
在△HAE和△BAE中,
,
∴△HAE≌△BAE(ASA)
∴AH=AB=6,HE=BE,
∵HE=BE,AD=DB,
∴DF AC,
∵HE=BE,
∴HC=2EF=2,
∴AC=AH+HC=8,
故答案为:C.
【分析】延长BE交AC于H,证明△HAE≌△BAE(ASA),根据全等三角形的性质求出AH,根据三角形中位线定理解答即可。
5.【答案】B
【解析】【解答】解:如图所示:
过点C作CM//AB,交AE的延长线于点M,交 AD 的延长线于点N,
∵CM//AB,
∴∠B=∠ECM,∠M=∠BAE,
∵BE=CE,
∴△ABE≌△MCE,
∴AB=CM=10,AE=EM,
∵AD 平分∠BAC,
∴∠BAD=∠CAD,
∵AB//CM,
∴∠BAD=∠ANC,
∴∠ANC=∠CAD,
∴AC-CN-6,
∴MN=4,
∵AC=CN,CF⊥AD,
∴AF=FN,
∵AE=EM,
∴,
故答案为:B.
【分析】根据平行线的性质先求出∠B=∠ECM,∠M=∠BAE,再利用全等三角形的判定与性质,角平分线的定义计算求解即可。
6.【答案】B
【解析】【解答】解:过点P作于点F,过点P作于点G,过点P作于点H,如图所示:
∵,为的角平分线,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∵,,
∴,
同理得:,
∴,,
∴,故B正确.
故答案为:B.
【分析】过点P作PF⊥BC于点F,过点P作PG⊥AC于点G,过点P作PH⊥AB于点H,由角平分线的性质可得PF=PG=PH,根据内角和定理可得∠ABC+∠ACB=120°,结合角平分线的概念可得∠PBF+∠PCF=(∠ABC+∠ACB)=60°,则∠BPC=120°,易得∠EPH=∠DPG,利用AAS证明△PEH≌△PDG,得到S△PEH=S△PDG,推出S四边形AEPD=S四边形AHPG=5,则S△PBH+S△PBF+S△PCF+S△PCG=S△ABC-S四边形AHPG=11,利用HL证明△CPF≌△CPG,得到S△BPH=S△BPF,S△CPF=S△CPG,据此计算.
7.【答案】D
【解析】【解答】解:如图所示:当点D在BP的延长线上时,
由作图可知,直线m是线段AB的垂直平分线,
∵点P在直线m上,
∴PA=PB,∠ABP=∠BAP,
∴APD=180°-x°=∠ABP+∠BAP=2∠ABP=2∠BAP,
∴∠ABP=∠BAP=90°-,
∵直线n与直线PB垂直,
∴∠ADP=90°,
∴∠DAP+∠BAP+∠ABP=90°,
∴y°+90°-+90°-=90°,
∴x°-y°=90°,
即x-y=90,
当点D在线段PB上时,如下图所示:
同理可得,x+y=90°,
故答案为:D.
【分析】分类讨论,结合图形,利用线段的垂直平分线,三角形内角和定理,三角形的外角的性质等计算求解即可。
8.【答案】C
【解析】【解答】解:如图所示:
由题意得HE=DG=1,GC=HB=4,∠EHB=∠DGC=90°,
∴△EHB≌△DGC(SAS),
∴∠EBH=∠DCG,
∵DB∥GC,
∴∠DBA=∠BAC,
∵,
∴,
∴,
故答案为:C
【分析】先根据题意即可得到HE=DG=1,GC=HB=4,∠EHB=∠DGC=90°,进而根据三角形全等的判定与性质证明△EHB≌△DGC(SAS)即可得到∠EBH=∠DCG,再根据平行线的性质即可得到∠DBA=∠BAC,进而结合题意得到,再结合题意即可求解。
9.【答案】A
【解析】【解答】解:A、已知两边AB、BC和其中BC的对角∠A,不能确定三角形ABC的形状和大小,符合题意;
B、已知两边AB、AC和它们的夹角∠A,能确定三角形ABC的形状和大小,不符合题意;
C、A、已知两角∠A、∠C和其中∠C的对边AB,能确定三角形ABC的形状和大小,不符合题意;
A、已知三边AB、BC和AC,能确定三角形ABC的形状和大小,不符合题意;
故答案为:A.
【分析】根据三角形全等的判定条件,进行判断即可。
10.【答案】D
【解析】【解答】解:∵DC=AC,EC=BC,∠DCE=∠ACB,
∴△ABC≌△DEC(SAS),
∴AB=DE,故乐乐的方案可行.
∵AB⊥BF,DE⊥BF,
∴∠ABC=90°,∠EDC=90°.
∵∠ABC=∠EDC,BC=CD,∠ACB=∠ECD,
∴△ABC≌△EDC(ASA),
∴AB=ED,故明明的方案可行.
∵BD⊥AB,
∴∠ABD=∠CBD.
∵∠ABD=∠CBD,BD=BD,∠BDC=∠BDA,
∴△ABD≌△CBD(ASA),
∴AB=BC,故聪聪的方案可行.
故答案为:D.
【分析】利用全等三角形的判定定理以及性质进行判断即可.
11.【答案】
【解析】【解答】解:延长AE到F,使EF=AE,连接DF
∵BE=DE,∠AEB=∠FED,AE=EF,
∴△ABE≌△FDE(SAS),
∴AB=DF,∠B=∠FDE.
∵CD=AB,
∴CD=DF.
∵∠BAD+∠B=90°,∠B+∠BAD+∠ADB=180°,
∴∠B+∠ADB=90°,
∴∠BAD=∠BDA.
∵∠ADC=∠B+∠BAD,∠ADF=∠FDE+∠BDA,∠BAD=∠BDA,
∴∠ADC=∠ADF.
又∵AD=AD,CD=DF,∠ADC=∠ADF,
∴△ADC≌△ADF(SAS),
∴AC=AF=AE+EF=2AE.
∵AE=,
∴AC=2AE=.
故答案为:.
【分析】延长AE到F,使EF=AE,连接DF,利用SAS证明⊿ABE≌⊿FDE,得到AB=DF,∠B=∠FDE,由已知条件可知CD=AB,则CD=DF,根据∠BAD+∠B=90°结合内角和定理可得∠B+∠ADB=90°,则∠BAD=∠BDA,由外角的性质可得∠ADC=∠B+∠BAD,根据角的和差关系可得∠ADF=∠FDE+∠BDA,进而推出∠ADC=∠ADF,利用SAS证明△ADC≌△ADF,得到AC=AF=AE+EF=2AE,据此计算.
12.【答案】①③④
【解析】【解答】解:①∵BE、CD为△ABC的角平分线 ,∴∴,又∵∠BAC=60°,∴∠ABC+∠ACB=180°-∠BAC=180°-60°=120°,∴∠FBC+∠FCB=60°∴∠BFC=180°-(∠FBC+∠FCB)=180°-60°=120°,所以①正确;
③如图3所示,在BC上截取BG=BD,在△BDF和△BGF中,BD=BG,∠DBF=∠GBF,BF=BF,∴△BDF≌△BGF,∴∠BFD=∠BFG,又∠BFD=180°-∠BFC=180°-120°=60°,∴∠BFG=60°,∴∠CFG=∠BFC-∠BFG=120°-60°=60°,又∠CFE=∠BFD=60°,∴∠CFG=∠CFE,又CF=CF,∠FCG=∠FCE,∴△CFG≌△CFE,∴CG=CE,∵BC=BG+CG
∴BC=BD+CE,所以③正确;
④已知点F是角平分线的交点,所以点F到各条边的距离相等,设点F到边的距离为h,则,,∴,由③知BC=BD+CE,∴,∴,所以④正确;
②假设BD=CE成立,由③知BC=BD+CE=2BD=2BG,即点G是BC的中点,又∠BFG=∠CFG,FG=FG,∴△BFG≌△CFG,∴∠FBG=∠FCG,∴∠ABC=∠ACB,∴△ABC是等腰三角形,又∠BAC=60°,∴△ABC是等边三角形,但已知△ABC并没有说是等边三角形,所以②结论不正确。综上,①③④正确。
故第1空答案为:①③④.
图3
【分析】根据角平分线的定义及三角形内角和可判定①正确;由反证法可说明②不正确;通过证明三角形全等可证得③结论正确;根据角平分线的性质可知点F到三边的距离相等,可得④正确,故可得出答案。
13.【答案】
【解析】【解答】解:∵∠A=α,
∴∠ABC+∠ACB=180°-α
又∵OB平分∠ABC,OC平分∠ACB
∴∠ABC=2∠OBC,∠ACB=2∠OCB
∴2∠OBC+2∠OCB=180°-α
∴
∴
∵BE平分∠OBC,CE平分∠OCD
∴,
∴
∴
故答案为.
【分析】要求∠E的度数,我们可以利用△BEC的外角∠ECD,因为∠E=∠ECD-∠EBC.而根据BE和CE分别是∠OBC和∠OCD的角平分线的性质,,,所以,即只要求出∠O的度数即可.利用∠A=α,利用三角形内角和为180°,得到∠ABC和∠ACB的度数和180°-α,OB和OC是∠ABC和∠ACB的角平分线,得到∠OBC和∠OCB的度数和,进而得到∠O的值,回代至即可.
14.【答案】160
【解析】【解答】解:如图1,连接,
∵在中,,
∴.
∵三内角的角平分线交于点D,
∴平分,
∴,
同理可得,,,
∵在中,
,
又∵,,,
∴,
∵,
∴.
如图2,连接,
∵三边的垂直平分线交于点E,
∴,
∴,,,
∵,,
∴,
∵,
∴,
∵,,
∴,
即,
∵,,
∴,
∵,
∴,
∵
∴,
∵,,
∴,
∴,
∴在中,
.
故答案为:160.
【分析】利用角平分线的性质,垂直平分线的性质和三角形的内角和求解即可。
15.【答案】25
【解析】【解答】解:如图示:
过点 ,分别作 交 于点 , 交 于点 , ,交 延长线于点 ,
∵ 平分 , 平分 ,
∴ , ,
∴ ,
∴ 平分 ,
∵ , ,
∴ ,
∴ ,
∵ 平分 ,
∴
在 和 中,
∴ ,
故答案为:25.
【分析】过点E,分别作 EF⊥BD于点E, EG⊥AC于点G,EH⊥AB交AB延长线于点H ,由角平分线上的点到角两边的距离相等得EH=EF=EG,根据三角形外角的性质得∠HAC=∠ABC+∠ACB=112°,由角平分线的定义得∠EAO=∠HAC,∠EBC=∠ABC,在△AOE和△BOC中, 由∠AEB=∠OBC+∠OCB-∠OAE即可求解.
16.【答案】 或
【解析】【解答】解:∵ , , ,
∴ ,
∵ 垂直平分AC,
∴ ,
∴ ,
∴ ,
同理 ,
,
可得第n条线段 的长为: 或 .
故答案为: 或 .
【分析】先求出 ,再求出,最后找出规律求解即可。
17.【答案】(1)解:以点A为圆心,以AB长为半径画弧交AD于一点,则此点为所要求的点P.
(2)解:线段BC、BF、CE之间的关系为:BC=BF+CE .
在BC上截取BD=BF.
在△BFO和△BDO中
∴△BFO≌△BDO
∴∠BOF=∠BOD
∵∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
∴∠BOC=180°- ∠ABC- ∠ACB=180° -60° =120°
∴∠BOD=∠BOF=∠COE=180°-120°=60° .
∠COD=∠BOC-∠BOD=120°-60° =60°
在△COE和△COD中
∴△COE≌△COD
∴CE=CD
∴BC=BF+CE .
(3)解:线段BC、BF、CE之间的关系为:BC=BF+CE .
在BC上截取BF'=BF.
在△BFO和△BF'O中
∴△BFO≌△BF'O
∴∠BOF=∠BOF'
∵∠A=60° ,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
∴∠BOC=180°- ∠ABC- ∠ACB=180°-60° =120°
∴∠BOF'=∠BOF=∠COE=180°-120°=60° .
∠COF'=∠BOC-∠BOF'=120° -60°=60°
在△COE和△COF'中
∴△COE≌△COF'
∴CE=CF'
∴BC=BF+CE .
【解析】【分析】(1)以点A为圆心,以AB长为半径画弧交AD于一点即可;(2)在BC上截取BD=BF,首先证明△BFO≌△BDO,创造条件证明△COE≌△COD即可;(3)在BC上截取BF'=BF,首先证明△BFO≌△BF'O,创造条件证明△COE≌△COF'即可.
18.【答案】解:四边形木架,至少要再钉上1根木条,使四边形变成两个三角形;
五边形木架,至少要再钉上2根木条,使五边形变成3个三角形;
六边形木架,至少要再钉上3根木条,使六边形变成4个三角形;
n边形木架,至少要再钉上(n﹣3)根木条,使多边形变成(n﹣2)个三角形
【解析】【分析】 根据三角形具有稳定性,主要是应用了三角形的稳定性,四边形木架,至少要再钉上1根木条;五边形木架,至少要再钉上2根木条;六边形木架,至少要再钉上3根木条;n边形木架,至少要再钉上(n﹣3)根木条.
19.【答案】解:当点F在边AC的延长线上时,延长EF、AD相交于点G,如图:
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠BAD=∠G,∠B=∠E,
∴∠CAD=∠G,
∴FA=FG,
在△ABD和△GED中,,
∴△ABD≌△GED(AAS),
∴AB=EG,
∴AF+EF=FG+EF=EG=AB;
当点F在边AC上,延长FE、AD相交于点H,如图:
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠BAD=∠H,∠B=∠DEH,
∴∠CAD=∠H,
∴FA=FH,
在△ABD和△HED中,,
∴△ABD≌△HED(AAS),
∴AB=EH,
∴AF-EF=FH-EF=EH=AB;
当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图:
延长AD交EF于点I,
∵AD是△ABC的外角平分线,
∴∠JAD=∠CAD,
∵EF∥AB,
∴∠JAD=∠AIF,∠B=∠E,
∴∠CAD=∠AIF,
∴FA=FI,
在△ABD和△IED中,,
∴△ABD≌△IED(SAS),
∴AB=EI,
∴EF- AF= EF-IF=EI=AB.
【解析】【分析】利用三角形的全等判定方法和性质求解即可。
20.【答案】证明:延长 至点 ,使得 ,连接 ,
四边形 中, , ,
,
在 和 中,
,
,
, ,
, ,
,
,
在 和 中,
,
,
.
【解析】【分析】延长 至点 ,使得 ,连接 ,根据同校的补角相等得出,根据SAS证明 ,则 , ,进而证明 ,根据SAS证明 ,得出ME=MN,则 .
21.【答案】(1)2t;(7-2t)
(2)解:△CAP≌△PBQ,PC⊥PQ,理由如下:
证明:点Q的运动速度与点P的运动速度相等,
当t=1时,AP=BQ=2cm,BP=7-2=5cm,
∵AC=5cm,
∴AC=BP,
∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,
在△CAP与△PBQ中,
∵AC=PB,∠A=∠B=90°,AP=BQ,
∴△CAP≌△PBQ(SAS),
∴∠ACP=∠BPQ,
∵∠ACP+∠CPA=90°,
∴∠BPQ+∠CPA=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(3)解:由题意得AP=2tcm,BP=AB-AP=(7-2t)cm,BQ=xtcm,
分类讨论:
①当△ACP≌△BPQ时,则AC=BP,AP=BQ,
∴5=7-2t且2t=tx,
解得x=2,t=1;
②若△ACP≌△BQP,则AC=BQ,AP=BP,
∴5=xt且2t=7-2t,
解得t=,x=,
综上当△ACP与△BPQ全等时,x的值为2或.
【解析】【解答】解:(1)AP=2tcm,BP=AB-AP=(7-2t)cm;
故答案为:2t,(7-2t);
【分析】(1)根据路程=速度×时间可表示出AP的长,进而根据BP=AB-AP可表示出BP;
(2)△CAP≌△PBQ,PC⊥PQ,理由如下:由题意易得AP=BQ,AC=BP,由垂直定义得∠A=∠B=90°,用SAS判断出△CAP≌△PBQ,得∠ACP=∠BPQ,从而由直角三角形两锐角互余、等量代换及平角定义可得∠CPQ=90°,根据垂直定义可得答案;
(3)由题意得AP=2tcm,BP=AB-AP=(7-2t)cm,BQ=xtcm,分类讨论:①当△ACP≌△BPQ时,则AC=BP,AP=BQ,②若△ACP≌△BQP,则AC=BQ,AP=BP,分别列出方程,求解可得答案.
22.【答案】(1)
(2)解:如图2,过点作
,即,
又,
,
,,
,
,
(3)解:
【解析】【解答】解(1)∵AM∥CN,AB⊥BC,
∴∠A+∠C=90°
故答案为:∠A+∠C=90°.
(3) 如图三作BG∥DM
设∠DBE=α,则∠DBC=2α+90°,∠BFC=3α.
则
∵BD⊥AM,
∴∠DFB=45°-α.
∴∠AFC=∠DFB+∠BFC=45°+2α.
∵∠FCB+∠NCF=180°,∠AFC+∠NCF=180°,
∴∠FCB=∠AFC=45°+2α.
由(2)知,∠NCB=2α,
∴2α+2(45°+2α) =180°,
解得α=15°.
∴∠EBC=90°+α=105°.
【分析】(1)已知AB⊥BC,由两直线平行同位角相等,即可推出∠A与∠C之间的数量关系;
(2)如图2作BG∥DM,然后根据同角的余角相等,可以得出∠ABD=∠CBG,再由平行线的性质,可以得出∠C=∠CBG,然后即可得∠ABD=∠C;
(3) 如图三作BG∥DM,然后设∠DBE=α,则∠DBC=2α+90°,∠BFC=3α,由BD⊥AM可以推出∠AFC=∠DFB+∠BFC=45°+2α,再由题上所给条件以及(2)中可得2α+2(45°+2α) =180°,然后解出α,求出∠EBC的度数.
23.【答案】(1)
(2)解:∵,,,
∴,
∴,
∴是的角平分线;
(3)解:如图,点即为所求作的点;
.
【解析】【解答】解:(1)∵DE=DE,CE=DE,CO=DO,
∴△EDO≌△ECO(SSS),
∴∠EOB=∠EOA,
∴就是的平分线,
故答案为:SSS
【分析】(1)根据三角形全等的判定(SSS)结合三角形全等的性质即可求解;
(2)先证明,进而即可得到,再根据角平分线的判定即可求解;
(3)根据题意画出∠CAB的角平分线,进而截取AE=AD即可求解。
24.【答案】(1)解:特例探究,
∵,
∴,
∴.
∵,∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(2)解:归纳证明:结论成立.
证明:
∵,
∴,
∴.
∵,∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(3)结论成立
(4)或
【解析】【分析】(1)先求出 ,再利用全等三角形的判定方法求出 ,最后证明求解即可;
(2)根据题意先求出 ,再利用SAS证明 ,最后证明求解即可;
(3)根据(1)(2)所求,找出规律求解即可;
(4)结合图形,利用三角形的面积公式计算求解即可。
班级: 姓名:
同学们:
练习开始了,希望你认真审题,细致做题,运用所学知识解决本练习。祝你收获满满,学习进步,榜上有名!
一、选择题
1.如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
A. 两点之间 B. 两点之间
C. 两点之间 D. 两点之间
2.阅读以下作图步骤:
①在和上分别截取,使;②分别以为圆心,以大于的长为半径作弧,两弧在内交于点;③作射线,连接,如图所示.根据以上作图,一定可以推得的结论是( )
A.且 B.且
C.且 D.且
3.如图,中,,,三条角平分线、、交于,于下列结论:;;平分;其中正确的结论个数有( )
A.1个 B.2个 C.3个 D.4个
4.如图,点E是△ABC内一点,∠AEB=90°,AE平分∠BAC,D是边AB的中点,延长线段DE交边BC于点F,若AB=6,EF=1,则线段AC的长为( )
A.7 B. C.8 D.9
5.如图,中,分别是其角平分线和中线,过点C作于F,连接,则线段的长为( )
A. B.2 C. D.3
6.如图,的角平分线,交于点,,的面积为16,四边形的面积为5,则的面积为( )
A.5 B.5.5 C.6 D.7
7.对于直线L和直线L外的一点O,按下列步骤完成了尺规作图:(1)在直线L的另一侧取点M;(2)以O为圆心,为半径作弧与L交于A,B两点;(3)分别以A,B为圆心,大于为半径作弧,两弧交于点C;(4)过点O和C作直线m.问题:“在直线m上任取一点P(点P不在L上),连接,,过点A作直线n与直线垂直,设是,直线n与所夹的锐角是,求x与y的数量关系.”下面是三个同学的答案,甲:,乙:,丙:.
对于三人的答案,下列结论正确的是( )
A.只有甲的答案正确 B.甲和乙的答案合在一起才正确
C.甲和丙的答案合在一起才正确 D.甲乙丙的答案合在一起才正确
8.如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点,若,则等于( )
A. B. C. D.
9.给定三角形的两个元素,画出的三角形的形状和大小都是不能确定的,在下列给定的条件下,再增加一个“”的条件后,所画出的三角形形状和大小仍不能完全确定的是( )
A., B.,
C., D.,
10.乐乐所在的七年级某班学生到野外活动,为测量池塘两端,的距离,乐乐、明明、聪聪三位同学分别设计出如下几种方案:
乐乐:如图,先在平地取一个可直接到达,的点,再连接,,并分别延长至,至,使,,最后测出的长即为,的距离.
明明:如图,先过点作的垂线,再在上取,两点,使,接着过点作的垂线,交的延长线于点,则测出的长即为,的距离.
聪聪:如图,过点作,再由点观测,在的延长线上取一点,使这时只要测出的长即为,的距离.
以上三位同学所设计的方案中可行的是( )
A.乐乐和明明 B.乐乐和聪聪
C.明明和聪聪 D.三人的方案都可行
二、填空题
11.如图,已知D是△ABC的边BC上一点,且,,AE是△ABD的中线,若,则 .
12.如图,在锐角中,,、为的角平分线.且、交于点,连接.有下列四个结论:①;②;③;④.其中结论正确的序号是 .
13.如图,在中,点O是和的平分线的交点,点D是BC延长线上的点,和的平分线交于点E,,则的度数为 .(用含的式子表示)
14.如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若,则 度.
15.在△ABC中,∠ABC=62°,∠ACB=50°,∠ACD是△ABC的外角 ∠ACD和∠ABC的平分线交于点E,则∠AEB=
16.如图,已知 中, , , ,作AC的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第一条线段 ;作 的垂直平分线交AB于点 、交AC于点 ,连接 ,得到第二条线段 ;作 的垂直平分线交AB于点 、交 于点 ,连接 ,得到第三条线段 ;……,如此作下去,则第n条线段 的长为 .
三、解答题
17.
(1)如图,AE是∠MAD的平分线,点C是AE上一点,点B是AM上一点,在AD上求作一点P,使得△ABC≌△APC,请保留清晰的作图痕迹.
(2)如图a,在△ABC中, ∠ACB= 90°,∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.请探究线段BC、BF、CE之间的关系,直接写出结论,不要求证明.
(3)如图b,若(2)中∠ACB为任意角,其它条件不变,请探究BC、BF、CE之间又有怎样的关系,请证明你的结论.
要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?
19.已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图3.写出AF、EF与AB的数量关系,并对图②进行证明.
20.如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
21.如图(1),,,垂足分别为、,点在线段上以的速度由点向点运动,同时点在射线上运动.它们运动的时间为当点运动结束时,点运动随之结束.
(1)AP , 用含的代数式表示;
(2)若点的运动速度与点的运动速度相等,当时,与是否全等,并判断此时线段和线段的位置关系,请分别说明理由;
(3)如图(2),若“,”改为“”,点的运动速度为,其它条件不变,当点、运动到何处时有与全等,求出相应的的值.
22.已知,点为平面内一点,于.
(1)如图1,直接写出和之间的数量关系 ;
(2)如图2,过点作于点,求证:;
(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分,平分,若,,直接写出的度数.
23.综合与实践
(1)问题探究:如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在和上分别取点C和D,使得,连接,以为边作等边三角形,则就是的平分线.
请写出平分的依据: ;
(2)类比迁移:
小明根据以上信息研究发现:不一定必须是等边三角形,只需即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在的边,上分别取,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线是的平分线,请说明此做法的理由;
(3)拓展实践:
小明将研究应用于实践.如图4,校园的两条小路和,汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
24.下面是张老师数学课堂教学实践活动的一个片段:
【问题背景】如图1,一副三角板的直角顶点重合,两条直角边分别共线,将它们分别记作,.其中,,,.现固定三角板,将三角板绕点A逆时针旋转,旋转角记为,射线与射线交于点P,在射线上取一点Q,使,连接CQ.
(1)【特例探究】如图2,当时,直接写出和的数量关系和位置关系.
(2)【归纳证明】如图3,当点P在线段BC上时,【特例探究】中得到的结论是否成立,若成立,请给出证明;若不成立,请说明理由.
(3)【类比迁移】当点P在线段延长线上时,请直接写出【特例探究】中结论是否成立,不必说明理由.
(4)【拓展应用】连接.若,的面积等于,请直接写出的长.
1.【答案】D
【解析】【解答】解:A.若钉在E,H两点之间构成了三角形,能固定窗框,故不符合题意;
B.若钉在A,C两点之间能构成三角形,能固定窗框,故不符合题意;
C.若钉在F,E两点之间能构成三角形,能固定窗框,故不符合题意;
D.若钉在E,G两点之间不能构成三角形,不能固定窗框,故符合题意;
故答案为:D.
【分析】利用三角形的定义判断求解即可。
2.【答案】A
【解析】【解答】解:由作图可得:CM=DM.
∵CM=DM,OC=OD,OM=OM,
∴△OCM≌△ODM(SSS),
∴∠1=∠2.
故答案为:A.
【分析】由作图可得:CM=DM,OC=OD,利用SSS证明△OCM≌△ODM,据此判断.
3.【答案】C
【解析】【解答】解: ,
,
,
, ,
,
故①正确;
于H ,
,
,
,
,
,
,
故②正确;
, ,
,
,
,
, ,
,
,
,
,
故③错误;
如图,在BC上截取BI=BF,连接OI ,
,
,
,
,
在△OBI和△OBF中,
,
∴△OBI≌△OBF(SAS)
,
,
,
,
在△CIO与△CEO中,
,
∴△CIO≌△CEO(ASA)
,
,
故④正确.
故答案为:C.
【分析】易得∠ABC+∠ACB=120°,由角平分线的概念可得∠OBC=∠ABC,∠OCB=∠ACB,则∠OBC+∠OCB=60°,利用内角和定理求出∠BOC的度数,据此判断①;根据余角的性质结合外角的性质可得∠DOH=90°-∠BAD-∠ABC,结合角平分线的概念以及内角和定理可得∠DOH=(∠ACB-∠ABC),进而判断②;易得∠ACB>60°,则∠ABC
【解析】【解答】解:延长BE交AC于H,
∵AE平分∠BAC,
∴∠HAE=∠BAE,
∵∠AEB=90°,
∴∠AEB=∠AEH=90°,
在△HAE和△BAE中,
,
∴△HAE≌△BAE(ASA)
∴AH=AB=6,HE=BE,
∵HE=BE,AD=DB,
∴DF AC,
∵HE=BE,
∴HC=2EF=2,
∴AC=AH+HC=8,
故答案为:C.
【分析】延长BE交AC于H,证明△HAE≌△BAE(ASA),根据全等三角形的性质求出AH,根据三角形中位线定理解答即可。
5.【答案】B
【解析】【解答】解:如图所示:
过点C作CM//AB,交AE的延长线于点M,交 AD 的延长线于点N,
∵CM//AB,
∴∠B=∠ECM,∠M=∠BAE,
∵BE=CE,
∴△ABE≌△MCE,
∴AB=CM=10,AE=EM,
∵AD 平分∠BAC,
∴∠BAD=∠CAD,
∵AB//CM,
∴∠BAD=∠ANC,
∴∠ANC=∠CAD,
∴AC-CN-6,
∴MN=4,
∵AC=CN,CF⊥AD,
∴AF=FN,
∵AE=EM,
∴,
故答案为:B.
【分析】根据平行线的性质先求出∠B=∠ECM,∠M=∠BAE,再利用全等三角形的判定与性质,角平分线的定义计算求解即可。
6.【答案】B
【解析】【解答】解:过点P作于点F,过点P作于点G,过点P作于点H,如图所示:
∵,为的角平分线,
∴,
∵,
∴,
∵,,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴,
∵,,
∴,
同理得:,
∴,,
∴,故B正确.
故答案为:B.
【分析】过点P作PF⊥BC于点F,过点P作PG⊥AC于点G,过点P作PH⊥AB于点H,由角平分线的性质可得PF=PG=PH,根据内角和定理可得∠ABC+∠ACB=120°,结合角平分线的概念可得∠PBF+∠PCF=(∠ABC+∠ACB)=60°,则∠BPC=120°,易得∠EPH=∠DPG,利用AAS证明△PEH≌△PDG,得到S△PEH=S△PDG,推出S四边形AEPD=S四边形AHPG=5,则S△PBH+S△PBF+S△PCF+S△PCG=S△ABC-S四边形AHPG=11,利用HL证明△CPF≌△CPG,得到S△BPH=S△BPF,S△CPF=S△CPG,据此计算.
7.【答案】D
【解析】【解答】解:如图所示:当点D在BP的延长线上时,
由作图可知,直线m是线段AB的垂直平分线,
∵点P在直线m上,
∴PA=PB,∠ABP=∠BAP,
∴APD=180°-x°=∠ABP+∠BAP=2∠ABP=2∠BAP,
∴∠ABP=∠BAP=90°-,
∵直线n与直线PB垂直,
∴∠ADP=90°,
∴∠DAP+∠BAP+∠ABP=90°,
∴y°+90°-+90°-=90°,
∴x°-y°=90°,
即x-y=90,
当点D在线段PB上时,如下图所示:
同理可得,x+y=90°,
故答案为:D.
【分析】分类讨论,结合图形,利用线段的垂直平分线,三角形内角和定理,三角形的外角的性质等计算求解即可。
8.【答案】C
【解析】【解答】解:如图所示:
由题意得HE=DG=1,GC=HB=4,∠EHB=∠DGC=90°,
∴△EHB≌△DGC(SAS),
∴∠EBH=∠DCG,
∵DB∥GC,
∴∠DBA=∠BAC,
∵,
∴,
∴,
故答案为:C
【分析】先根据题意即可得到HE=DG=1,GC=HB=4,∠EHB=∠DGC=90°,进而根据三角形全等的判定与性质证明△EHB≌△DGC(SAS)即可得到∠EBH=∠DCG,再根据平行线的性质即可得到∠DBA=∠BAC,进而结合题意得到,再结合题意即可求解。
9.【答案】A
【解析】【解答】解:A、已知两边AB、BC和其中BC的对角∠A,不能确定三角形ABC的形状和大小,符合题意;
B、已知两边AB、AC和它们的夹角∠A,能确定三角形ABC的形状和大小,不符合题意;
C、A、已知两角∠A、∠C和其中∠C的对边AB,能确定三角形ABC的形状和大小,不符合题意;
A、已知三边AB、BC和AC,能确定三角形ABC的形状和大小,不符合题意;
故答案为:A.
【分析】根据三角形全等的判定条件,进行判断即可。
10.【答案】D
【解析】【解答】解:∵DC=AC,EC=BC,∠DCE=∠ACB,
∴△ABC≌△DEC(SAS),
∴AB=DE,故乐乐的方案可行.
∵AB⊥BF,DE⊥BF,
∴∠ABC=90°,∠EDC=90°.
∵∠ABC=∠EDC,BC=CD,∠ACB=∠ECD,
∴△ABC≌△EDC(ASA),
∴AB=ED,故明明的方案可行.
∵BD⊥AB,
∴∠ABD=∠CBD.
∵∠ABD=∠CBD,BD=BD,∠BDC=∠BDA,
∴△ABD≌△CBD(ASA),
∴AB=BC,故聪聪的方案可行.
故答案为:D.
【分析】利用全等三角形的判定定理以及性质进行判断即可.
11.【答案】
【解析】【解答】解:延长AE到F,使EF=AE,连接DF
∵BE=DE,∠AEB=∠FED,AE=EF,
∴△ABE≌△FDE(SAS),
∴AB=DF,∠B=∠FDE.
∵CD=AB,
∴CD=DF.
∵∠BAD+∠B=90°,∠B+∠BAD+∠ADB=180°,
∴∠B+∠ADB=90°,
∴∠BAD=∠BDA.
∵∠ADC=∠B+∠BAD,∠ADF=∠FDE+∠BDA,∠BAD=∠BDA,
∴∠ADC=∠ADF.
又∵AD=AD,CD=DF,∠ADC=∠ADF,
∴△ADC≌△ADF(SAS),
∴AC=AF=AE+EF=2AE.
∵AE=,
∴AC=2AE=.
故答案为:.
【分析】延长AE到F,使EF=AE,连接DF,利用SAS证明⊿ABE≌⊿FDE,得到AB=DF,∠B=∠FDE,由已知条件可知CD=AB,则CD=DF,根据∠BAD+∠B=90°结合内角和定理可得∠B+∠ADB=90°,则∠BAD=∠BDA,由外角的性质可得∠ADC=∠B+∠BAD,根据角的和差关系可得∠ADF=∠FDE+∠BDA,进而推出∠ADC=∠ADF,利用SAS证明△ADC≌△ADF,得到AC=AF=AE+EF=2AE,据此计算.
12.【答案】①③④
【解析】【解答】解:①∵BE、CD为△ABC的角平分线 ,∴∴,又∵∠BAC=60°,∴∠ABC+∠ACB=180°-∠BAC=180°-60°=120°,∴∠FBC+∠FCB=60°∴∠BFC=180°-(∠FBC+∠FCB)=180°-60°=120°,所以①正确;
③如图3所示,在BC上截取BG=BD,在△BDF和△BGF中,BD=BG,∠DBF=∠GBF,BF=BF,∴△BDF≌△BGF,∴∠BFD=∠BFG,又∠BFD=180°-∠BFC=180°-120°=60°,∴∠BFG=60°,∴∠CFG=∠BFC-∠BFG=120°-60°=60°,又∠CFE=∠BFD=60°,∴∠CFG=∠CFE,又CF=CF,∠FCG=∠FCE,∴△CFG≌△CFE,∴CG=CE,∵BC=BG+CG
∴BC=BD+CE,所以③正确;
④已知点F是角平分线的交点,所以点F到各条边的距离相等,设点F到边的距离为h,则,,∴,由③知BC=BD+CE,∴,∴,所以④正确;
②假设BD=CE成立,由③知BC=BD+CE=2BD=2BG,即点G是BC的中点,又∠BFG=∠CFG,FG=FG,∴△BFG≌△CFG,∴∠FBG=∠FCG,∴∠ABC=∠ACB,∴△ABC是等腰三角形,又∠BAC=60°,∴△ABC是等边三角形,但已知△ABC并没有说是等边三角形,所以②结论不正确。综上,①③④正确。
故第1空答案为:①③④.
图3
【分析】根据角平分线的定义及三角形内角和可判定①正确;由反证法可说明②不正确;通过证明三角形全等可证得③结论正确;根据角平分线的性质可知点F到三边的距离相等,可得④正确,故可得出答案。
13.【答案】
【解析】【解答】解:∵∠A=α,
∴∠ABC+∠ACB=180°-α
又∵OB平分∠ABC,OC平分∠ACB
∴∠ABC=2∠OBC,∠ACB=2∠OCB
∴2∠OBC+2∠OCB=180°-α
∴
∴
∵BE平分∠OBC,CE平分∠OCD
∴,
∴
∴
故答案为.
【分析】要求∠E的度数,我们可以利用△BEC的外角∠ECD,因为∠E=∠ECD-∠EBC.而根据BE和CE分别是∠OBC和∠OCD的角平分线的性质,,,所以,即只要求出∠O的度数即可.利用∠A=α,利用三角形内角和为180°,得到∠ABC和∠ACB的度数和180°-α,OB和OC是∠ABC和∠ACB的角平分线,得到∠OBC和∠OCB的度数和,进而得到∠O的值,回代至即可.
14.【答案】160
【解析】【解答】解:如图1,连接,
∵在中,,
∴.
∵三内角的角平分线交于点D,
∴平分,
∴,
同理可得,,,
∵在中,
,
又∵,,,
∴,
∵,
∴.
如图2,连接,
∵三边的垂直平分线交于点E,
∴,
∴,,,
∵,,
∴,
∵,
∴,
∵,,
∴,
即,
∵,,
∴,
∵,
∴,
∵
∴,
∵,,
∴,
∴,
∴在中,
.
故答案为:160.
【分析】利用角平分线的性质,垂直平分线的性质和三角形的内角和求解即可。
15.【答案】25
【解析】【解答】解:如图示:
过点 ,分别作 交 于点 , 交 于点 , ,交 延长线于点 ,
∵ 平分 , 平分 ,
∴ , ,
∴ ,
∴ 平分 ,
∵ , ,
∴ ,
∴ ,
∵ 平分 ,
∴
在 和 中,
∴ ,
故答案为:25.
【分析】过点E,分别作 EF⊥BD于点E, EG⊥AC于点G,EH⊥AB交AB延长线于点H ,由角平分线上的点到角两边的距离相等得EH=EF=EG,根据三角形外角的性质得∠HAC=∠ABC+∠ACB=112°,由角平分线的定义得∠EAO=∠HAC,∠EBC=∠ABC,在△AOE和△BOC中, 由∠AEB=∠OBC+∠OCB-∠OAE即可求解.
16.【答案】 或
【解析】【解答】解:∵ , , ,
∴ ,
∵ 垂直平分AC,
∴ ,
∴ ,
∴ ,
同理 ,
,
可得第n条线段 的长为: 或 .
故答案为: 或 .
【分析】先求出 ,再求出,最后找出规律求解即可。
17.【答案】(1)解:以点A为圆心,以AB长为半径画弧交AD于一点,则此点为所要求的点P.
(2)解:线段BC、BF、CE之间的关系为:BC=BF+CE .
在BC上截取BD=BF.
在△BFO和△BDO中
∴△BFO≌△BDO
∴∠BOF=∠BOD
∵∠A= 60°,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
∴∠BOC=180°- ∠ABC- ∠ACB=180° -60° =120°
∴∠BOD=∠BOF=∠COE=180°-120°=60° .
∠COD=∠BOC-∠BOD=120°-60° =60°
在△COE和△COD中
∴△COE≌△COD
∴CE=CD
∴BC=BF+CE .
(3)解:线段BC、BF、CE之间的关系为:BC=BF+CE .
在BC上截取BF'=BF.
在△BFO和△BF'O中
∴△BFO≌△BF'O
∴∠BOF=∠BOF'
∵∠A=60° ,BE、CF分别是∠ABC和∠ACB的角平分线,CF与BE相交于点O.
∴∠BOC=180°- ∠ABC- ∠ACB=180°-60° =120°
∴∠BOF'=∠BOF=∠COE=180°-120°=60° .
∠COF'=∠BOC-∠BOF'=120° -60°=60°
在△COE和△COF'中
∴△COE≌△COF'
∴CE=CF'
∴BC=BF+CE .
【解析】【分析】(1)以点A为圆心,以AB长为半径画弧交AD于一点即可;(2)在BC上截取BD=BF,首先证明△BFO≌△BDO,创造条件证明△COE≌△COD即可;(3)在BC上截取BF'=BF,首先证明△BFO≌△BF'O,创造条件证明△COE≌△COF'即可.
18.【答案】解:四边形木架,至少要再钉上1根木条,使四边形变成两个三角形;
五边形木架,至少要再钉上2根木条,使五边形变成3个三角形;
六边形木架,至少要再钉上3根木条,使六边形变成4个三角形;
n边形木架,至少要再钉上(n﹣3)根木条,使多边形变成(n﹣2)个三角形
【解析】【分析】 根据三角形具有稳定性,主要是应用了三角形的稳定性,四边形木架,至少要再钉上1根木条;五边形木架,至少要再钉上2根木条;六边形木架,至少要再钉上3根木条;n边形木架,至少要再钉上(n﹣3)根木条.
19.【答案】解:当点F在边AC的延长线上时,延长EF、AD相交于点G,如图:
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠BAD=∠G,∠B=∠E,
∴∠CAD=∠G,
∴FA=FG,
在△ABD和△GED中,,
∴△ABD≌△GED(AAS),
∴AB=EG,
∴AF+EF=FG+EF=EG=AB;
当点F在边AC上,延长FE、AD相交于点H,如图:
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠BAD=∠H,∠B=∠DEH,
∴∠CAD=∠H,
∴FA=FH,
在△ABD和△HED中,,
∴△ABD≌△HED(AAS),
∴AB=EH,
∴AF-EF=FH-EF=EH=AB;
当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图:
延长AD交EF于点I,
∵AD是△ABC的外角平分线,
∴∠JAD=∠CAD,
∵EF∥AB,
∴∠JAD=∠AIF,∠B=∠E,
∴∠CAD=∠AIF,
∴FA=FI,
在△ABD和△IED中,,
∴△ABD≌△IED(SAS),
∴AB=EI,
∴EF- AF= EF-IF=EI=AB.
【解析】【分析】利用三角形的全等判定方法和性质求解即可。
20.【答案】证明:延长 至点 ,使得 ,连接 ,
四边形 中, , ,
,
在 和 中,
,
,
, ,
, ,
,
,
在 和 中,
,
,
.
【解析】【分析】延长 至点 ,使得 ,连接 ,根据同校的补角相等得出,根据SAS证明 ,则 , ,进而证明 ,根据SAS证明 ,得出ME=MN,则 .
21.【答案】(1)2t;(7-2t)
(2)解:△CAP≌△PBQ,PC⊥PQ,理由如下:
证明:点Q的运动速度与点P的运动速度相等,
当t=1时,AP=BQ=2cm,BP=7-2=5cm,
∵AC=5cm,
∴AC=BP,
∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,
在△CAP与△PBQ中,
∵AC=PB,∠A=∠B=90°,AP=BQ,
∴△CAP≌△PBQ(SAS),
∴∠ACP=∠BPQ,
∵∠ACP+∠CPA=90°,
∴∠BPQ+∠CPA=90°,
∴∠CPQ=90°,
∴PC⊥PQ;
(3)解:由题意得AP=2tcm,BP=AB-AP=(7-2t)cm,BQ=xtcm,
分类讨论:
①当△ACP≌△BPQ时,则AC=BP,AP=BQ,
∴5=7-2t且2t=tx,
解得x=2,t=1;
②若△ACP≌△BQP,则AC=BQ,AP=BP,
∴5=xt且2t=7-2t,
解得t=,x=,
综上当△ACP与△BPQ全等时,x的值为2或.
【解析】【解答】解:(1)AP=2tcm,BP=AB-AP=(7-2t)cm;
故答案为:2t,(7-2t);
【分析】(1)根据路程=速度×时间可表示出AP的长,进而根据BP=AB-AP可表示出BP;
(2)△CAP≌△PBQ,PC⊥PQ,理由如下:由题意易得AP=BQ,AC=BP,由垂直定义得∠A=∠B=90°,用SAS判断出△CAP≌△PBQ,得∠ACP=∠BPQ,从而由直角三角形两锐角互余、等量代换及平角定义可得∠CPQ=90°,根据垂直定义可得答案;
(3)由题意得AP=2tcm,BP=AB-AP=(7-2t)cm,BQ=xtcm,分类讨论:①当△ACP≌△BPQ时,则AC=BP,AP=BQ,②若△ACP≌△BQP,则AC=BQ,AP=BP,分别列出方程,求解可得答案.
22.【答案】(1)
(2)解:如图2,过点作
,即,
又,
,
,,
,
,
(3)解:
【解析】【解答】解(1)∵AM∥CN,AB⊥BC,
∴∠A+∠C=90°
故答案为:∠A+∠C=90°.
(3) 如图三作BG∥DM
设∠DBE=α,则∠DBC=2α+90°,∠BFC=3α.
则
∵BD⊥AM,
∴∠DFB=45°-α.
∴∠AFC=∠DFB+∠BFC=45°+2α.
∵∠FCB+∠NCF=180°,∠AFC+∠NCF=180°,
∴∠FCB=∠AFC=45°+2α.
由(2)知,∠NCB=2α,
∴2α+2(45°+2α) =180°,
解得α=15°.
∴∠EBC=90°+α=105°.
【分析】(1)已知AB⊥BC,由两直线平行同位角相等,即可推出∠A与∠C之间的数量关系;
(2)如图2作BG∥DM,然后根据同角的余角相等,可以得出∠ABD=∠CBG,再由平行线的性质,可以得出∠C=∠CBG,然后即可得∠ABD=∠C;
(3) 如图三作BG∥DM,然后设∠DBE=α,则∠DBC=2α+90°,∠BFC=3α,由BD⊥AM可以推出∠AFC=∠DFB+∠BFC=45°+2α,再由题上所给条件以及(2)中可得2α+2(45°+2α) =180°,然后解出α,求出∠EBC的度数.
23.【答案】(1)
(2)解:∵,,,
∴,
∴,
∴是的角平分线;
(3)解:如图,点即为所求作的点;
.
【解析】【解答】解:(1)∵DE=DE,CE=DE,CO=DO,
∴△EDO≌△ECO(SSS),
∴∠EOB=∠EOA,
∴就是的平分线,
故答案为:SSS
【分析】(1)根据三角形全等的判定(SSS)结合三角形全等的性质即可求解;
(2)先证明,进而即可得到,再根据角平分线的判定即可求解;
(3)根据题意画出∠CAB的角平分线,进而截取AE=AD即可求解。
24.【答案】(1)解:特例探究,
∵,
∴,
∴.
∵,∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(2)解:归纳证明:结论成立.
证明:
∵,
∴,
∴.
∵,∴.
在△ABP和△ACQ中,
∴.
∴,.
∴.
∴.
(3)结论成立
(4)或
【解析】【分析】(1)先求出 ,再利用全等三角形的判定方法求出 ,最后证明求解即可;
(2)根据题意先求出 ,再利用SAS证明 ,最后证明求解即可;
(3)根据(1)(2)所求,找出规律求解即可;
(4)结合图形,利用三角形的面积公式计算求解即可。
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
