浙教版八年级上册 5.4 一次函数的图象与性质(2)教案(表格式)
文档属性
| 名称 | 浙教版八年级上册 5.4 一次函数的图象与性质(2)教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 324.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-09 09:00:45 | ||
图片预览


文档简介
5.4一次函数的图象与性质(2)教学设计
课题 5.4一次函数的图象与性质(2)
学习目标 知识目标 1.利用函数图象了解一次函数的性质2.会根据自变量的取值范围求一次函数的取值范围3.会利用一次函数的图象和性质解决简单的实际问题
能力目标 在例题探究、合作学习的过程中培养自主探究的能力
情感态度和价值观目标 感受一次函数在生活中的妙用,具备数形结合解决问题的思维,感受数学的乐趣
重点 一次函数的性质
难点 一次函数的应用
学法 探究法 教法 讲授法
教学过程
教学环节 教师活动 学生活动 设计意图
回顾旧知 函数的图象的画法:列表 (2)描点(3)连线2.函数图象与坐标轴的交点令x=0,解出y的值即直线与y轴交点的纵坐标;令y=0,解出x的值即直线与x轴交点的横坐标. 回忆思考 帮助学生巩固所学,并引入新课
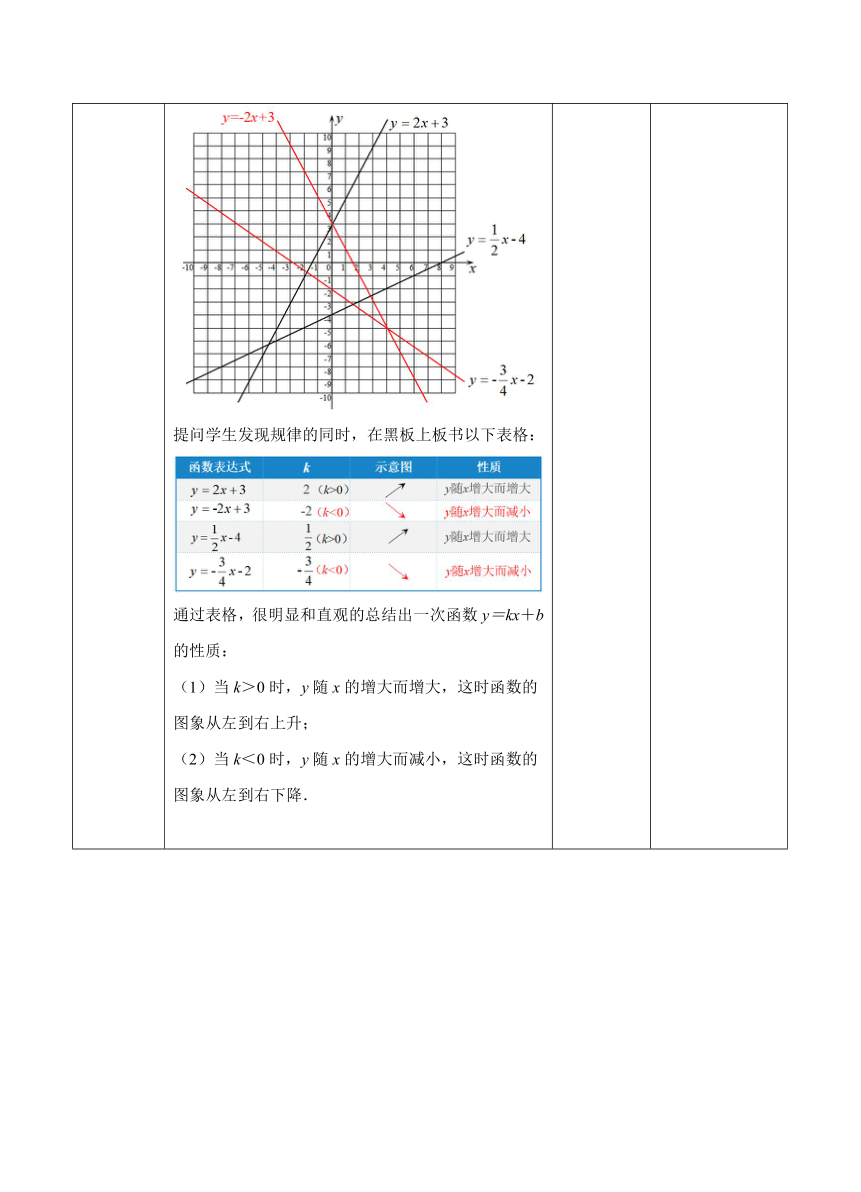
合作学习 要求学生画一次函数y=2x+3的图象,并且思考当自变量x的值增大时,函数y的值有什么变化?然后再给出y=-2x+3、 、 的图象,并且问学生:观察图中各个一次函数的图象,你发现了什么规律?提问学生发现规律的同时,在黑板上板书以下表格:通过表格,很明显和直观的总结出一次函数y=kx+b的性质:(1)当k>0时,y随x的增大而增大,这时函数的图象从左到右上升; (2)当k<0时,y随x的增大而减小,这时函数的图象从左到右下降. 观察思考 通过实例让学生发现规律
小试牛刀 1.设下列两个函数当x=x1时,y=y1;当x=x2时,y=y2 . 用“>”或“<”号填空: 对于函数 ,若x2>x1,则y2 y1, 对于函数 ,若x2 x1则y2<y1.设计意图:通过本题,主要让学生掌握在运用一次函数增减性解决问题时,需把增减性转换成数学符号的表示形式:y随x的增大而增大:x2>x1 y2>y1 y随x的增大而减小: x2>x1 y2学以致用 例:我国某地区现有人工造林面积12万公顷,规划今后每年新增造林p万公顷.6年后,该地区的造林总面积达到S万公顷.(1)求S关于p的函数表达式.(2)当0.5≤p≤0.6时,求S的取值范围.设计意图:把书本例题做了小小修改,变成了两小题,减小了本道题的难度,使学生更容易运用刚刚学习的性质解决,有助于学生学习的主动性和信心. 听课 讲解一次函数图象的性质的应用
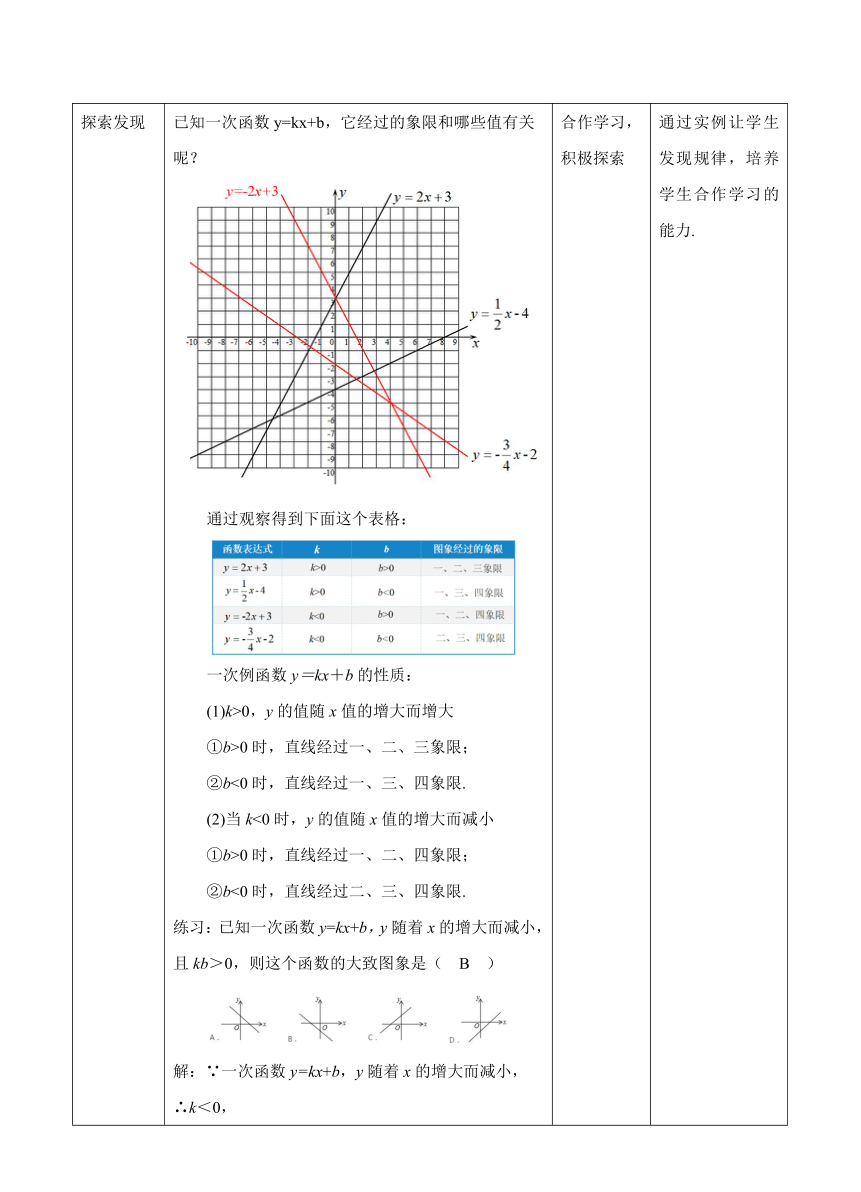
探索发现 已知一次函数y=kx+b,它经过的象限和哪些值有关呢?通过观察得到下面这个表格:一次例函数y=kx+b的性质:(1)k>0,y的值随x值的增大而增大①b>0时,直线经过一、二、三象限;②b<0时,直线经过一、三、四象限.(2)当k<0时,y的值随x值的增大而减小①b>0时,直线经过一、二、四象限;②b<0时,直线经过二、三、四象限.练习:已知一次函数y=kx+b,y随着x的增大而减小,且kb>0,则这个函数的大致图象是( B )解:∵一次函数y=kx+b,y随着x的增大而减小,
∴k<0,
∴一次函数y=kx+b的图象经过第二、四象限;
∵kb>0,
∴b<0,
∴图象与y轴的交点在x轴下方,
∴一次函数y=kx+b的图象经过第二、三、四象限.
故选B. 合作学习,积极探索 通过实例让学生发现规律,培养学生合作学习的能力.
课堂检测 1.一次函数y=-2x-3图象上两点P1(x1,y1),P2(x2,y2).若x1>x2,则y1与y2的大小关系是( ) ∵一次函数y=-2x-3中k=-2<0,
∴此函数是减函数,
∵x1>x2,
∴y1<y2.
故选C.2.若函数y=-x+b的图象不经过第一象限,则常数b的取值是( ) A.b>0B.b<0C.b≥0D.b≤0当一次函数y=-x+b的图象不经过第一象限时,
此时可能会出现如下两种情况:
①一次函数经过第二四象限,此时b=0;
②一次函数经过第二三四象限,此时b<0;
故选D.3.在平面直角坐标系中,已知直线y=mx+n(m<0,n>0),若点A(-2,y1)、(-3,y2)、C(1,y3)在直线y=mx+n上,则y1、y2、y3的大小关系为:__ y3<y1<y2(请用“<”符号连接).∵直线y=mx+n中,m<0,n>0,
∴此直线经过一、二、四象限,
∴y随x的增大而减小,
∵-3<-2<1,
∴y3<y1<y2.
故答案为:y3<y1<y2.4.已知一次函数y=(3-k)x-2k2+18,
(1)k为何值时,它的图象经过原点;
(2)k为何值时,它的图象经过点(0,-2);
(3)k为何值时,y随x的增大而减小.解:(1)∵图象经过原点,
∴点(0,0)在函数图象上,代入图象解析式得:0=-2k2+18,
解得:k=±3.
又∵y=(3-k)x-2k2+18是一次函数,
∴3-k≠0,
∴k≠3.
故k=-3.(2)∵图象经过点(0,-2),
∴点(0,-2)满足函数解析式,代入得:-2=-2k2+18,
解得:k=±. (3)∵y随x的增大而减小,
∴根据一次函数图象性质知,系数小于0,即3-k<0,
解得:k>3.5.有一个附有进水管、出水管的水池,每单位时间内进出水管的进、出水量都是一定的,设从某时刻开始,4h内只进水不出水,在随后的时间内不进水只出水,得到的时间x(h)与水量y(m3)之间的关系图(如图),回答下列问题:
(1)进水管4h共进水多少?每小时进水多少?
(2)当0≤x≤4时,y与x有何关系?
(3)当x=9时,水池中的水量是多少?
(4)若4h后,只放水不进水,那么多少小时可将水池中的水放完?解:(1)由图象知,4h共进水20m3,所以每小时进水量为5m3
(2)y是x的正比例函数,设y=kx,由于其图象过点(4,20),所以20=4k,k=5,即y=5x(0≤x≤4) (3)由图象可知:当x=9时y=10,即水池中的水量为10m3
(4)由于x≥4时,图象是一条直线,所以y是x的一次函数,设y=kx+b,由图象可知,该直线过点(4,20),(9,10)∴ 20=4k+b 解得 k=-2 10=9k+b b=28∴y= -2x+28
令y=0,则-2x+28=0,∴x=14
14-4=10,所以4h后,只放水不进水,10h就可以把水池里的水放完。 做题 通过做对应的题目,来让学生更深刻理解本节知识
课堂小结 这节课我们学习了:1.一次函数图象的性质对于一次函数y=kx+b(k、b为常数,且k≠0),当k>0时,y随着x的增大而增大;这时函数的图象从左到右上升; 当k<0时,y随着x的增大而减小;这时函数的图象从左到右下降。2.求最大值和最小值的方法:(1)利用图象(2)利用一次函数的增减性 回忆总结 带领学生回忆本课所学
布置作业 A组:作业本基础练习1,2,3,4B组:作业本:1,2,3,4,5,6 分层作业 有利于学生个人发展
D. y= –2x-7
C. y=5x– 4
A. y=–3x
B. y= –0.5x+1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
课题 5.4一次函数的图象与性质(2)
学习目标 知识目标 1.利用函数图象了解一次函数的性质2.会根据自变量的取值范围求一次函数的取值范围3.会利用一次函数的图象和性质解决简单的实际问题
能力目标 在例题探究、合作学习的过程中培养自主探究的能力
情感态度和价值观目标 感受一次函数在生活中的妙用,具备数形结合解决问题的思维,感受数学的乐趣
重点 一次函数的性质
难点 一次函数的应用
学法 探究法 教法 讲授法
教学过程
教学环节 教师活动 学生活动 设计意图
回顾旧知 函数的图象的画法:列表 (2)描点(3)连线2.函数图象与坐标轴的交点令x=0,解出y的值即直线与y轴交点的纵坐标;令y=0,解出x的值即直线与x轴交点的横坐标. 回忆思考 帮助学生巩固所学,并引入新课
合作学习 要求学生画一次函数y=2x+3的图象,并且思考当自变量x的值增大时,函数y的值有什么变化?然后再给出y=-2x+3、 、 的图象,并且问学生:观察图中各个一次函数的图象,你发现了什么规律?提问学生发现规律的同时,在黑板上板书以下表格:通过表格,很明显和直观的总结出一次函数y=kx+b的性质:(1)当k>0时,y随x的增大而增大,这时函数的图象从左到右上升; (2)当k<0时,y随x的增大而减小,这时函数的图象从左到右下降. 观察思考 通过实例让学生发现规律
小试牛刀 1.设下列两个函数当x=x1时,y=y1;当x=x2时,y=y2 . 用“>”或“<”号填空: 对于函数 ,若x2>x1,则y2 y1, 对于函数 ,若x2 x1则y2<y1.设计意图:通过本题,主要让学生掌握在运用一次函数增减性解决问题时,需把增减性转换成数学符号的表示形式:y随x的增大而增大:x2>x1 y2>y1 y随x的增大而减小: x2>x1 y2
探索发现 已知一次函数y=kx+b,它经过的象限和哪些值有关呢?通过观察得到下面这个表格:一次例函数y=kx+b的性质:(1)k>0,y的值随x值的增大而增大①b>0时,直线经过一、二、三象限;②b<0时,直线经过一、三、四象限.(2)当k<0时,y的值随x值的增大而减小①b>0时,直线经过一、二、四象限;②b<0时,直线经过二、三、四象限.练习:已知一次函数y=kx+b,y随着x的增大而减小,且kb>0,则这个函数的大致图象是( B )解:∵一次函数y=kx+b,y随着x的增大而减小,
∴k<0,
∴一次函数y=kx+b的图象经过第二、四象限;
∵kb>0,
∴b<0,
∴图象与y轴的交点在x轴下方,
∴一次函数y=kx+b的图象经过第二、三、四象限.
故选B. 合作学习,积极探索 通过实例让学生发现规律,培养学生合作学习的能力.
课堂检测 1.一次函数y=-2x-3图象上两点P1(x1,y1),P2(x2,y2).若x1>x2,则y1与y2的大小关系是( ) ∵一次函数y=-2x-3中k=-2<0,
∴此函数是减函数,
∵x1>x2,
∴y1<y2.
故选C.2.若函数y=-x+b的图象不经过第一象限,则常数b的取值是( ) A.b>0B.b<0C.b≥0D.b≤0当一次函数y=-x+b的图象不经过第一象限时,
此时可能会出现如下两种情况:
①一次函数经过第二四象限,此时b=0;
②一次函数经过第二三四象限,此时b<0;
故选D.3.在平面直角坐标系中,已知直线y=mx+n(m<0,n>0),若点A(-2,y1)、(-3,y2)、C(1,y3)在直线y=mx+n上,则y1、y2、y3的大小关系为:__ y3<y1<y2(请用“<”符号连接).∵直线y=mx+n中,m<0,n>0,
∴此直线经过一、二、四象限,
∴y随x的增大而减小,
∵-3<-2<1,
∴y3<y1<y2.
故答案为:y3<y1<y2.4.已知一次函数y=(3-k)x-2k2+18,
(1)k为何值时,它的图象经过原点;
(2)k为何值时,它的图象经过点(0,-2);
(3)k为何值时,y随x的增大而减小.解:(1)∵图象经过原点,
∴点(0,0)在函数图象上,代入图象解析式得:0=-2k2+18,
解得:k=±3.
又∵y=(3-k)x-2k2+18是一次函数,
∴3-k≠0,
∴k≠3.
故k=-3.(2)∵图象经过点(0,-2),
∴点(0,-2)满足函数解析式,代入得:-2=-2k2+18,
解得:k=±. (3)∵y随x的增大而减小,
∴根据一次函数图象性质知,系数小于0,即3-k<0,
解得:k>3.5.有一个附有进水管、出水管的水池,每单位时间内进出水管的进、出水量都是一定的,设从某时刻开始,4h内只进水不出水,在随后的时间内不进水只出水,得到的时间x(h)与水量y(m3)之间的关系图(如图),回答下列问题:
(1)进水管4h共进水多少?每小时进水多少?
(2)当0≤x≤4时,y与x有何关系?
(3)当x=9时,水池中的水量是多少?
(4)若4h后,只放水不进水,那么多少小时可将水池中的水放完?解:(1)由图象知,4h共进水20m3,所以每小时进水量为5m3
(2)y是x的正比例函数,设y=kx,由于其图象过点(4,20),所以20=4k,k=5,即y=5x(0≤x≤4) (3)由图象可知:当x=9时y=10,即水池中的水量为10m3
(4)由于x≥4时,图象是一条直线,所以y是x的一次函数,设y=kx+b,由图象可知,该直线过点(4,20),(9,10)∴ 20=4k+b 解得 k=-2 10=9k+b b=28∴y= -2x+28
令y=0,则-2x+28=0,∴x=14
14-4=10,所以4h后,只放水不进水,10h就可以把水池里的水放完。 做题 通过做对应的题目,来让学生更深刻理解本节知识
课堂小结 这节课我们学习了:1.一次函数图象的性质对于一次函数y=kx+b(k、b为常数,且k≠0),当k>0时,y随着x的增大而增大;这时函数的图象从左到右上升; 当k<0时,y随着x的增大而减小;这时函数的图象从左到右下降。2.求最大值和最小值的方法:(1)利用图象(2)利用一次函数的增减性 回忆总结 带领学生回忆本课所学
布置作业 A组:作业本基础练习1,2,3,4B组:作业本:1,2,3,4,5,6 分层作业 有利于学生个人发展
D. y= –2x-7
C. y=5x– 4
A. y=–3x
B. y= –0.5x+1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
