3.2实数

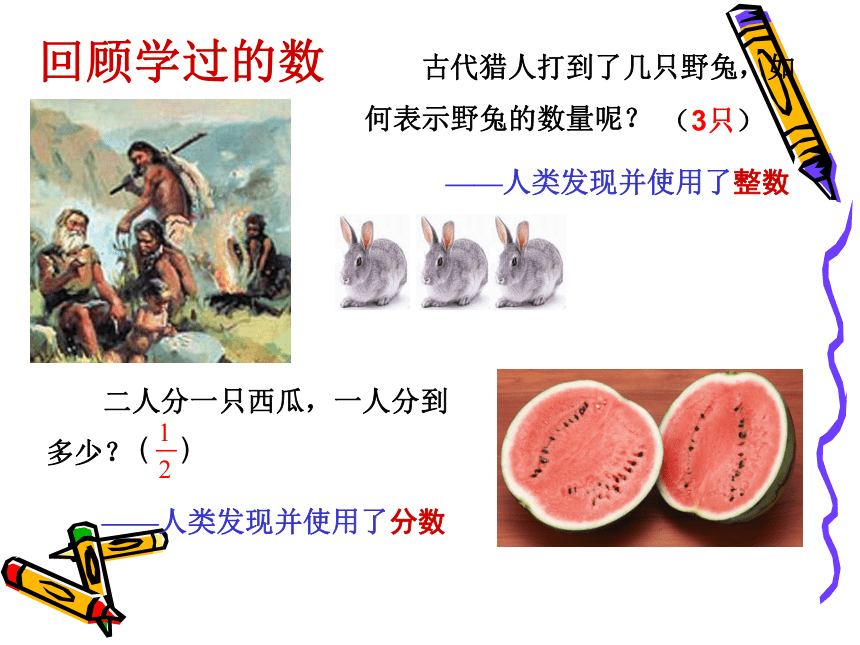
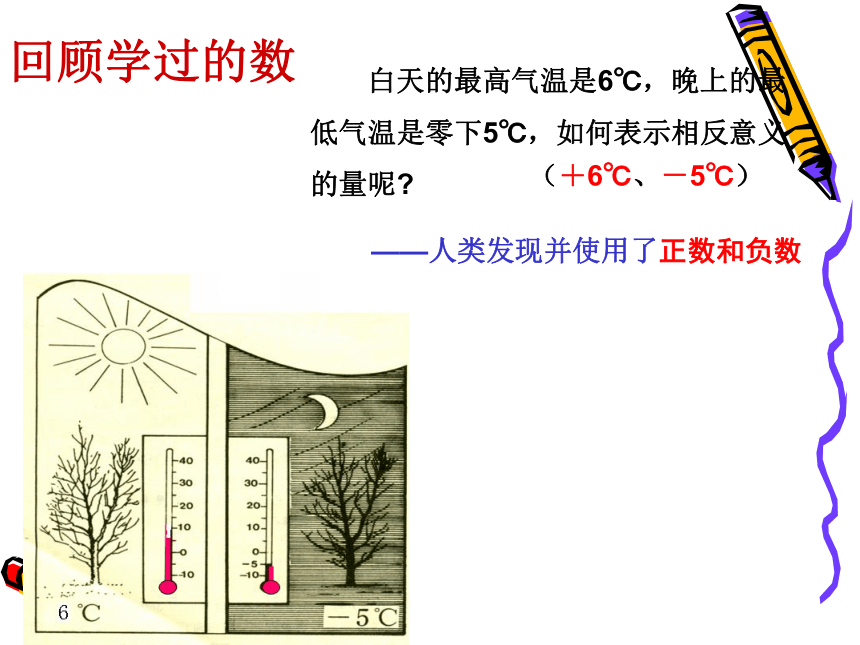
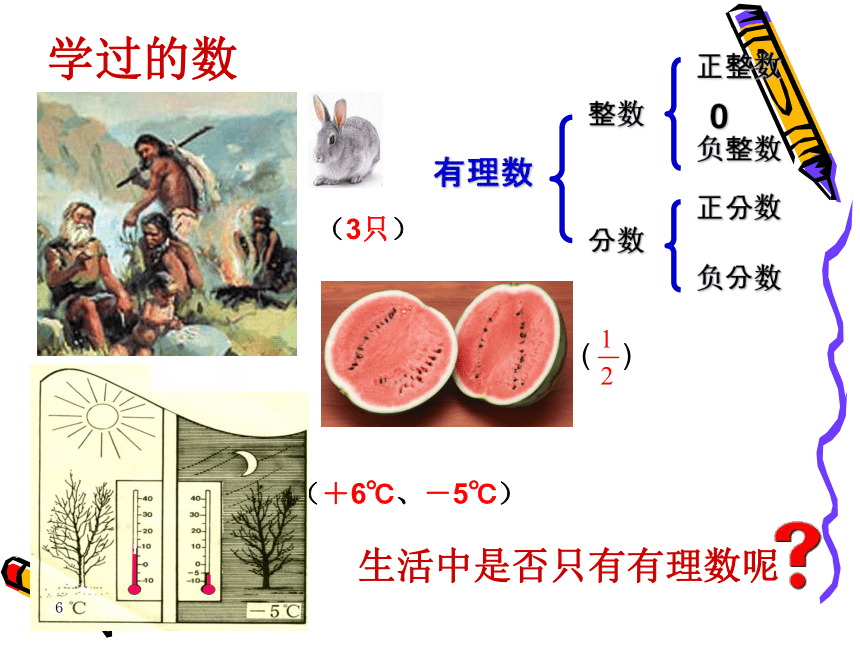
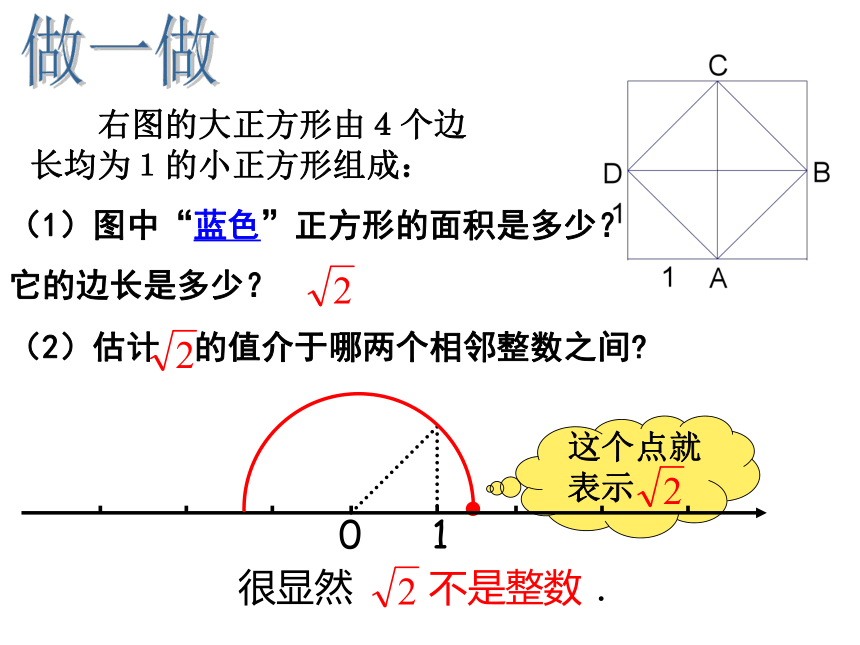
课件24张PPT。3.2 实数 二人分一只西瓜，一人分到多少？ 回顾学过的数 古代猎人打到了几只野兔，如何表示野兔的数量呢？——人类发现并使用了整数 ——人类发现并使用了分数（3只）( ) 白天的最高气温是6℃，晚上的最低气温是零下5℃，如何表示相反意义的量呢?——人类发现并使用了正数和负数 （＋6℃、－5℃）回顾学过的数学过的数生活中是否只有有理数呢（3只）( ) （＋6℃、－5℃）做一做　　右图的大正方形由４个边长均为１的小正方形组成：很显然　　不是整数．（1）图中“蓝色”正方形的面积是多少？
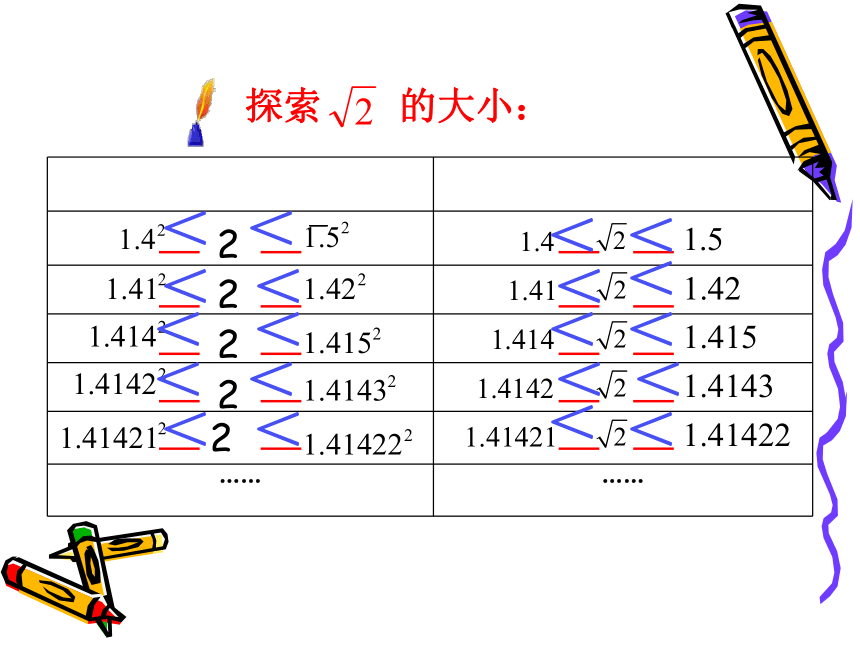
它的边长是多少？ 探索　　的大小：22222＜＜＜＜＜＜＜＜＜＜＜＜＜＜＜＜＜＜＜＜通过上述方法，
我们得出一系列越来越接近 的近似值现在，你对这个数有什么体会吗？1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605714701095599716059702745345968620147285174186408891986095523292304843087143214508397626036279952514079896872533965463318088296406206152583523950547457502877599617298355752203375318570113543746034084988471603868999706990048150305440277903164542478230684929369186215805784631115966687130130156185689872372352885092648612494977154218334204285686060146824720771435854874155657069677653720226485447015858801620758474922657226002085584466521458398893944370926591800311388246468157082630100594858704003186480342194897278290641045072636881313739855256117322040245091227700226941127573627280495738108967504018369868368450725799364729060762996941380475654823728997180326802474420629269124859052181004459842150591120249441341728531478105803603371077309182869314710171111683 9165817268894197587 ……与这些数有什么不同？它既不是有限小数，
也不是无限循环小数所以， 不是有理数　　　既不是有限小数，也不是无限循环小数，因此，　不是分数．
　　　不是有理数，它是一个无限不循环小数．像 这种无限不循环小数叫做无理数（irrational number）. 无理数广泛存在着，无理数一般有三种情况：①如 等，但 等是有理数；② 等；③1.010010001…（两个1之间依次多一个0），
95.6868868886…（两个6之间依次多一个8）等.0.12345678910111213 …(小数部分有相继的正整数组成)练习．下列说法正确吗？请说明理由。
（1）无理数是无限小数;
（2）有理数是有限小数；
（3）无限小数是无理数；
（4）有理数都是实数，实数都是有理数；
（5）无理数是带根号的数；
（6）带根号的数都是无理数； 和有理数一样，无理数也可分为正无理数和负无理数。例如：都是正无理数，都是负无理数。正有理数负有理数零负无理数正无理数有理数无理数实 数有理数和无理数统称为实数（real number）．无限不循环小数有限小数和
无限循环小数 把数从有理数扩充到实数以后，有理数的相反数和绝对值的概念同样适用于实数。例如： 和 互为相反数
∵
∴绝对值等于 的数是　 和
知识拓展填空：
（1） 的相反数是__________
（2） 的相反数是
（3） ___________
（4）绝对值等于 的数是 _________ 同步冲刺
在实数范围内，每一个实数都可以用数轴上的点来表示； 实数与数轴上的点一一对应。反过来，数轴上的每一个点都表示一个实数。能力冲浪 数轴上的每一个点都表示一个有理数吗？无理数是否也可以在数轴上表示？ 在数轴上表示的两个实数，右边的数总比左边的数大。能力冲浪例:把下列实数表示在数轴上,并比较它们的大小(用“<”号连接) 在哪两个整数之间3.3-1.41.5， ， ， ， ， 解:由图得
属于有理数的有：_______________；
属于无理数的有：_________________________；
属于负数的有：___________
属于实数的有：___________________________.课内练习 （2） 的相反数是_________； 的相反数是__________.（3） ________； _________；（4）一个数的绝对值是 ，则这个数是_____.探究学习 1、判断下列说法是否正确，并举例说明理由.
①两个无理数的和一定是无理数；
②两个无理数的积一定是无理数；
③两个无理数的商可能是有理数. 思考题利用如图4×4方格，作出面积为8平方单位的正方形，然后在数轴上表示实数 和 。归纳总结1、无理数和实数的概念；2、实数的分类；3、实数和数轴上的点是一一对应的；4、相反数、绝对值、数的大小比较法则同样适用于实数；注意：实数不是一个完全陌生的数，前面学过的有理数是实数的一部分，只不过增加了一个新成员——无理数。“海神错判” 约公元600年，毕达哥拉斯学派认为宇宙万物的总规律是服从整数化，认为世界上一切现象，都能归结为整数或整数之比。正当毕氏学派津津乐道地高唱“万物皆数”时，该学派的一位成员希伯索斯利用推理的方法发现，边长为1的正方形的对角线长既不是整数，也不是整数的比（分数）所能表示的.这个发现被人们看成是“荒谬”和违反常识的事。对于只有整数和整数比概念的他们来说，这意味着边长为1的正方形的对角线长竟然不能用任何“数”来表示！这在数学史上称为第一次数学危机。最后希伯索斯的发现没有被毕达哥拉斯学派的信徒所接受，相传就因为这一发现，毕达哥拉斯学派把希伯索斯投入大海中处死。 再 见 !