第一章二次函数练习题(含详解)2024-2025学年浙教版八年级数学上册
文档属性
| 名称 | 第一章二次函数练习题(含详解)2024-2025学年浙教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 416.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-10 18:58:49 | ||
图片预览


文档简介
第一章二次函数练习题
一、单选题
1.将抛物线向右平移2个单位,再向下平移6个单位,得到的抛物线的表达式为( )
A. B.
C. D.
2.抛物线y=2(x+1)2-5的顶点坐标是( )
A.(1,-5) B.(-1,-5) C.(-1,-4) D.(-2,-7)
3.抛物线的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.把抛物线向右平移个单位,再向上平移个单位,得到的抛物线是( )
A. B. C. D.
5.函数的图象与轴的交点坐标为( ).
A. B. C. D.
6.已知二次函数的图象的对称轴为直线,其图象如图所示,现有下列结论:①;②;③;④;⑤.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
7.如图,抛物线与x轴交于点A,B,与y轴交于点C,对称轴为直线,若点A的坐标为,则下列结论正确的是( )
A.
B.
C.是关于x的一元二次方程的一个根
D.点,在抛物线上,当时
二、填空题
8.已知二次函数,若当x取,(≠)时,函数值相等,则当x取+时,函数值为 .
9.当或()时,二次函数的函数值相等,则时,代数式的值为 .
10.2019年在武汉市举行了军运会.在军运会比赛中,某次羽毛球的运动路线可以看作是抛物线的一部分(如图),其中出球点B离地面O点的距离是1米,球落地点A到O点的距离是 .
11.已知的图象经过点和,且当时,有,则a的取值范围是 .
12.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-1,下列结论:① b2>4ac;② abc>0;③ a-c<0;④ am2+bm≥a-b(m为任意实数),其中正确的结论是
三、解答题
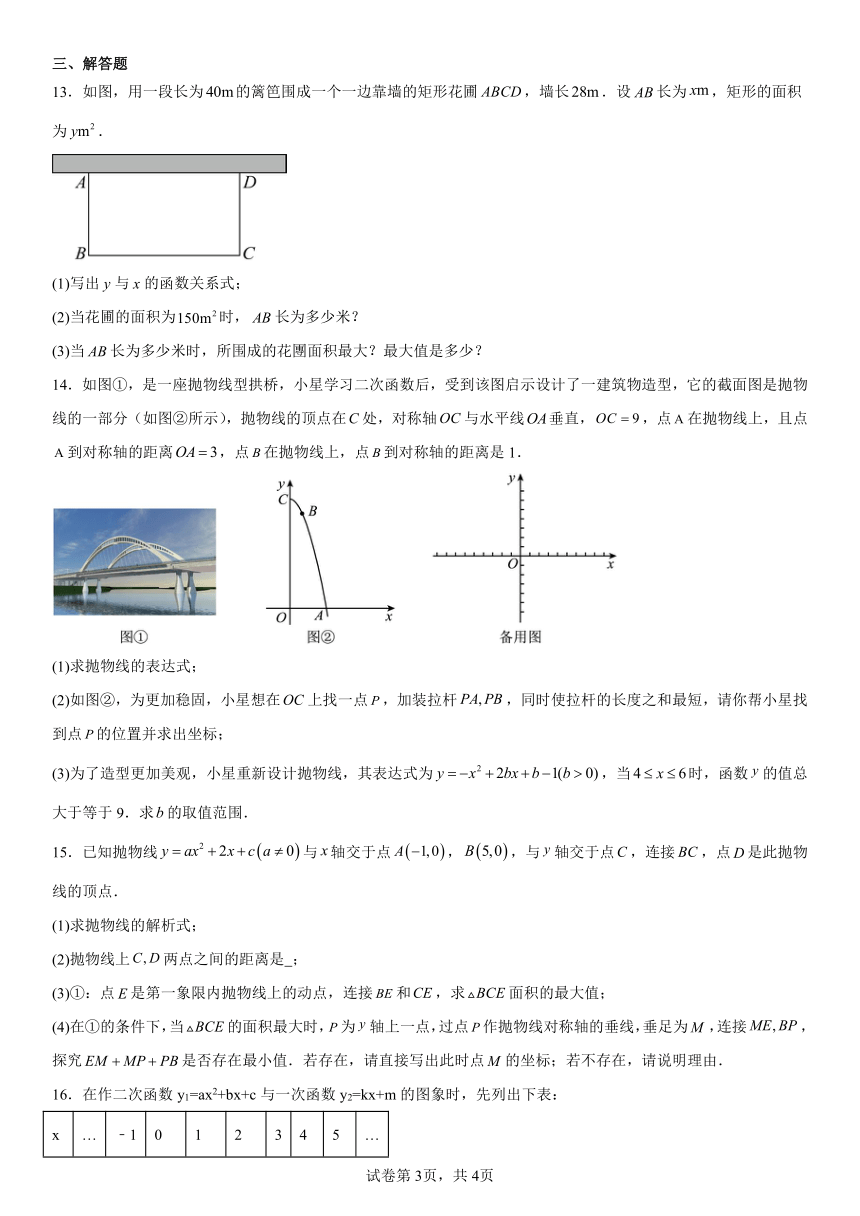
13.如图,用一段长为的篱笆围成一个一边靠墙的矩形花圃,墙长.设长为,矩形的面积为.
(1)写出y与x的函数关系式;
(2)当花圃的面积为时,长为多少米?
(3)当长为多少米时,所围成的花團面积最大?最大值是多少?
14.如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在上找一点,加装拉杆,同时使拉杆的长度之和最短,请你帮小星找到点的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为,当时,函数的值总大于等于9.求的取值范围.
15.已知抛物线与轴交于点,,与轴交于点,连接,点是此抛物线的顶点.
(1)求抛物线的解析式;
(2)抛物线上两点之间的距离是 ;
(3)①:点是第一象限内抛物线上的动点,连接和,求面积的最大值;
(4)在①的条件下,当的面积最大时,为轴上一点,过点作抛物线对称轴的垂线,垂足为,连接,探究是否存在最小值.若存在,请直接写出此时点的坐标;若不存在,请说明理由.
16.在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x … ﹣1 0 1 2 3 4 5 …
y1 … 0 ﹣3 ﹣4 ﹣3 0 5 12 …
y2 … 0 2 4 6 8 10 12 …
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为 ;
(2)当y1>y2时,自变量x的取值范围是 ;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.
17.在一场篮球比赛中,队员甲在距篮下4m处跳起投篮,出手的高度为2.25m,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5m.已知球篮中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中.
(2)此时,若对方队员乙在甲前面1.5m处跳起盖帽拦截,已知乙队员的最大摸高为3.1m,那么他能否拦截成功?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7
答案 A B A A C D C
1.A
【知识点】二次函数图象的平移
2.B
【知识点】y=a(x-h) +k的图象和性质
3.A
【知识点】y=a(x-h) +k的图象和性质
4.A
【知识点】二次函数图象的平移
5.C
【知识点】求抛物线与y轴的交点坐标
6.D
【知识点】根据二次函数的图象判断式子符号、二次函数图象与各项系数符号
7.C
【知识点】y=ax +bx+c的图象与性质、根据二次函数的图象判断式子符号、根据二次函数图象确定相应方程根的情况
8.-3.
【知识点】y=ax +k的图象和性质
9.5
【知识点】y=ax +bx+c的图象与性质
10.4m
【知识点】投球问题(实际问题与二次函数)
11.≤a<0或0<a≤.
12.①②④.
【知识点】根据二次函数的图象判断式子符号
13.(1)
(2)当长为时,面积为
(3)当长为时,花圃面积最大,最大面积为
【知识点】图形问题(实际问题与二次函数)、与图形有关的问题(一元二次方程的应用)
14.(1)
(2)点的坐标为
(3)
【知识点】待定系数法求二次函数解析式、y=ax +bx+c的图象与性质、拱桥问题(实际问题与二次函数)、根据成轴对称图形的特征进行求解
15.(1)
(2)
(3)
(4)存在,
【知识点】用勾股定理解三角形、其他问题(实际问题与二次函数)、y=ax +bx+c的图象与性质、待定系数法求二次函数解析式
16.(1)(0,﹣3);(2)当x<﹣1或x>5时,二次函数的值大于一次函数的值.(3)见解析
【知识点】y=ax +bx+c的图象与性质
17.(1),能准确投中
(2)乙不能拦截成功,利用见解析
【知识点】投球问题(实际问题与二次函数)、待定系数法求二次函数解析式
答案第1页,共2页
答案第1页,共2页
一、单选题
1.将抛物线向右平移2个单位,再向下平移6个单位,得到的抛物线的表达式为( )
A. B.
C. D.
2.抛物线y=2(x+1)2-5的顶点坐标是( )
A.(1,-5) B.(-1,-5) C.(-1,-4) D.(-2,-7)
3.抛物线的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.把抛物线向右平移个单位,再向上平移个单位,得到的抛物线是( )
A. B. C. D.
5.函数的图象与轴的交点坐标为( ).
A. B. C. D.
6.已知二次函数的图象的对称轴为直线,其图象如图所示,现有下列结论:①;②;③;④;⑤.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
7.如图,抛物线与x轴交于点A,B,与y轴交于点C,对称轴为直线,若点A的坐标为,则下列结论正确的是( )
A.
B.
C.是关于x的一元二次方程的一个根
D.点,在抛物线上,当时
二、填空题
8.已知二次函数,若当x取,(≠)时,函数值相等,则当x取+时,函数值为 .
9.当或()时,二次函数的函数值相等,则时,代数式的值为 .
10.2019年在武汉市举行了军运会.在军运会比赛中,某次羽毛球的运动路线可以看作是抛物线的一部分(如图),其中出球点B离地面O点的距离是1米,球落地点A到O点的距离是 .
11.已知的图象经过点和,且当时,有,则a的取值范围是 .
12.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-1,下列结论:① b2>4ac;② abc>0;③ a-c<0;④ am2+bm≥a-b(m为任意实数),其中正确的结论是
三、解答题
13.如图,用一段长为的篱笆围成一个一边靠墙的矩形花圃,墙长.设长为,矩形的面积为.
(1)写出y与x的函数关系式;
(2)当花圃的面积为时,长为多少米?
(3)当长为多少米时,所围成的花團面积最大?最大值是多少?
14.如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在处,对称轴与水平线垂直,,点在抛物线上,且点到对称轴的距离,点在抛物线上,点到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在上找一点,加装拉杆,同时使拉杆的长度之和最短,请你帮小星找到点的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为,当时,函数的值总大于等于9.求的取值范围.
15.已知抛物线与轴交于点,,与轴交于点,连接,点是此抛物线的顶点.
(1)求抛物线的解析式;
(2)抛物线上两点之间的距离是 ;
(3)①:点是第一象限内抛物线上的动点,连接和,求面积的最大值;
(4)在①的条件下,当的面积最大时,为轴上一点,过点作抛物线对称轴的垂线,垂足为,连接,探究是否存在最小值.若存在,请直接写出此时点的坐标;若不存在,请说明理由.
16.在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x … ﹣1 0 1 2 3 4 5 …
y1 … 0 ﹣3 ﹣4 ﹣3 0 5 12 …
y2 … 0 2 4 6 8 10 12 …
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为 ;
(2)当y1>y2时,自变量x的取值范围是 ;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.
17.在一场篮球比赛中,队员甲在距篮下4m处跳起投篮,出手的高度为2.25m,球运行的路线是抛物线,当球运行的水平距离为2.5m时,达到最大高度3.5m.已知球篮中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中.
(2)此时,若对方队员乙在甲前面1.5m处跳起盖帽拦截,已知乙队员的最大摸高为3.1m,那么他能否拦截成功?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7
答案 A B A A C D C
1.A
【知识点】二次函数图象的平移
2.B
【知识点】y=a(x-h) +k的图象和性质
3.A
【知识点】y=a(x-h) +k的图象和性质
4.A
【知识点】二次函数图象的平移
5.C
【知识点】求抛物线与y轴的交点坐标
6.D
【知识点】根据二次函数的图象判断式子符号、二次函数图象与各项系数符号
7.C
【知识点】y=ax +bx+c的图象与性质、根据二次函数的图象判断式子符号、根据二次函数图象确定相应方程根的情况
8.-3.
【知识点】y=ax +k的图象和性质
9.5
【知识点】y=ax +bx+c的图象与性质
10.4m
【知识点】投球问题(实际问题与二次函数)
11.≤a<0或0<a≤.
12.①②④.
【知识点】根据二次函数的图象判断式子符号
13.(1)
(2)当长为时,面积为
(3)当长为时,花圃面积最大,最大面积为
【知识点】图形问题(实际问题与二次函数)、与图形有关的问题(一元二次方程的应用)
14.(1)
(2)点的坐标为
(3)
【知识点】待定系数法求二次函数解析式、y=ax +bx+c的图象与性质、拱桥问题(实际问题与二次函数)、根据成轴对称图形的特征进行求解
15.(1)
(2)
(3)
(4)存在,
【知识点】用勾股定理解三角形、其他问题(实际问题与二次函数)、y=ax +bx+c的图象与性质、待定系数法求二次函数解析式
16.(1)(0,﹣3);(2)当x<﹣1或x>5时,二次函数的值大于一次函数的值.(3)见解析
【知识点】y=ax +bx+c的图象与性质
17.(1),能准确投中
(2)乙不能拦截成功,利用见解析
【知识点】投球问题(实际问题与二次函数)、待定系数法求二次函数解析式
答案第1页,共2页
答案第1页,共2页
同课章节目录
