3.2 实数

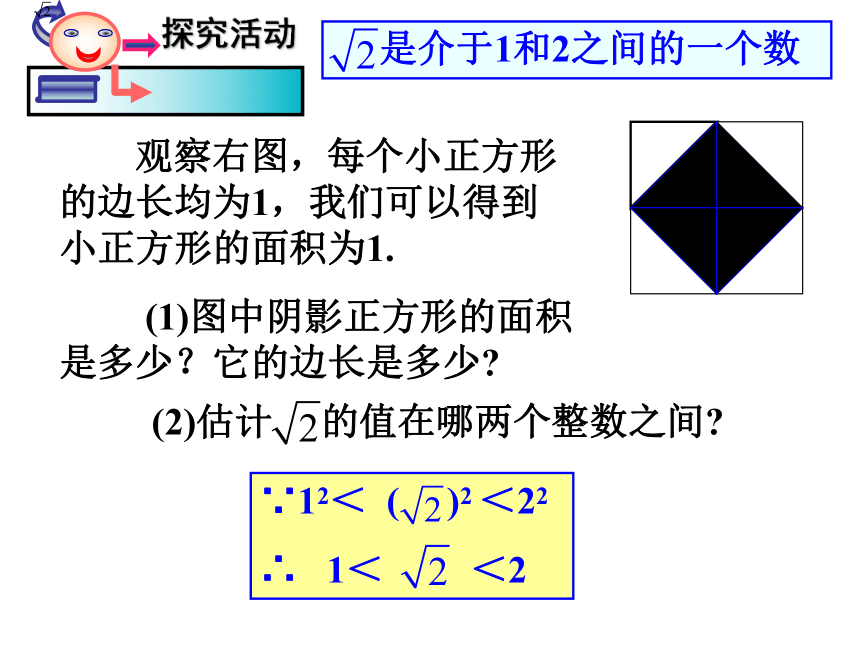
课件21张PPT。复习回顾1、请说说你的理解：§ 3.2 实数 观察右图，每个小正方形的边长均为1，我们可以得到小正方形的面积为1.
(1)图中阴影正方形的面积是多少？它的边长是多少?(2)估计 的值在哪两个整数之间? ∵12＜ ( )2 ＜22
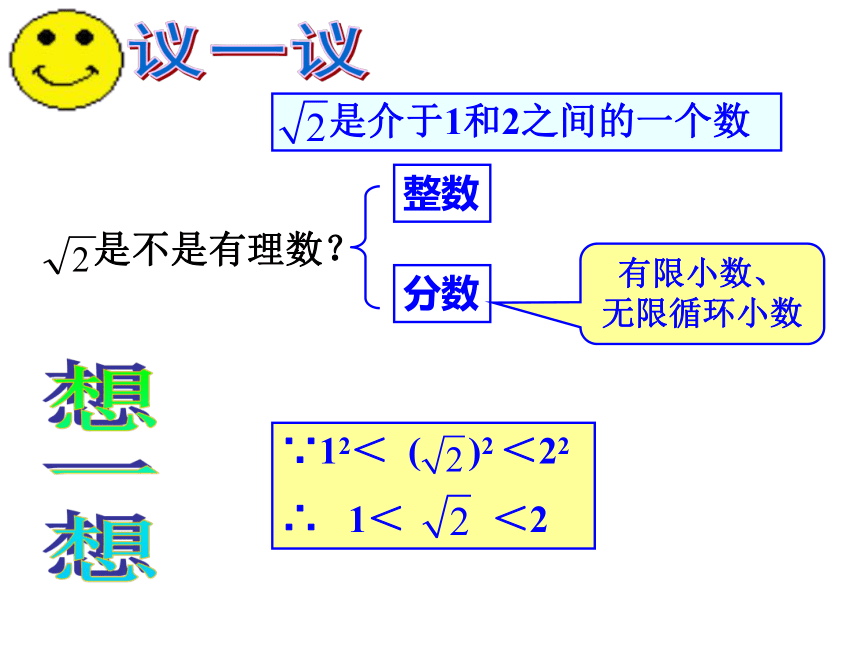
∴ 1＜ ＜2 是介于1和2之间的一个数是不是有理数？整数分数议一议有限小数、
无限循环小数 是介于1和2之间的一个数∵12＜ ( )2 ＜22
∴ 1＜ ＜2想一想合作学习 是介于1和2之间的一个数，请在表中的空白处填上适当的不等号. 概念像 这种无限不循环小数叫做无理数。举例（2）π=3.141592653589793…
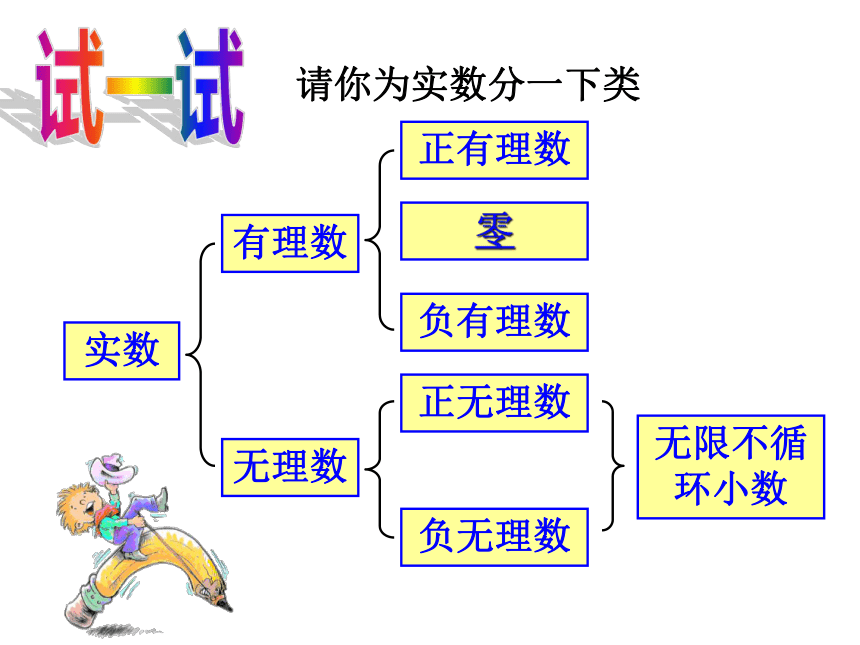
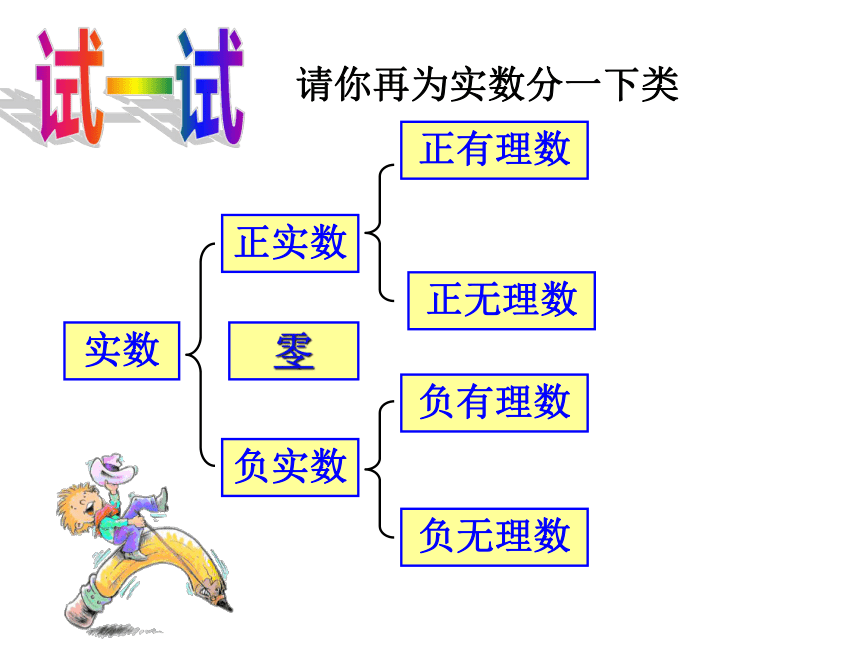
2×π、3＋π……（3）任意写一个无限不循环小数，如1.010010001…（两个“1”之间依次多个“0”）正无理数负无理数无限不循环的小数无理数：理一理有理数和无理数统称实数试一试请你为实数分一下类实数有理数无理数正有理数零负有理数正无理数负无理数无限不循环小数试一试请你再为实数分一下类实数正实数负实数正有理数零正无理数负有理数负无理数在 中属于有理数的有：__________________;属于无理数的有：________________;属于实数的有：______________________.做一做注意 把数从有理数扩充到实数以后，有理数中的相反数和绝对值的概念同样适用于实数。课内练习 2、一个数的绝对值是 ，则这个数是______.1、求下列各数的绝对值和相反数：
（1） ； （2） ； （3）－π例把下列实数表示在数轴上，并用“＜”号连接：＊π在数轴上表示的是它的近似值。
＊数轴上的点可以表示无理数。
＊你会利用数轴比较实数的大小吗？－1.41.53.3结论 （1）在实数范围内，每一个数都可以用数轴上的点来表示；反过来，数轴上的每一个点都表示一个实数。我们说实数和数轴上的点一一对应。
（2）在数轴上表示的两个实数，
右边的数总比左边的数大。练一练用“＜” ，“＞”，或数字填空：＜＜＜＜（1）∵1.732____( )2 ____1.742
∴ 1.73 ____ ( ) ____1.74
∴ ≈______（保留2个有效数字）1.7（2）∵2.4492____( )2 ____2.4502
∴ 2.449____ ( ) ____2.450
∴ ≈______（保留3个有效数字）＜＜＜＜2.45小结你知道什么是实数了吗？
你会给实数分类了吗？
你能写出几个无理数吗？（1） 的相反数是____（2）___的相反数是（3） ＝____（4）绝对值等于 的数是_____拓 展 1、填空2、填空拓 展 （1）到原点距离为 个单位的点表示的数是_____（2） _________（3） 的相反数是 _________，绝对值是__________3、判断下列说法是否正确，并举例说明理由。
（1）两个无理数的和一定是无理数；
（2）两个无理数的积一定是无理数；
（3）带根号的数都是无理数；
（4）数轴上的点和有理数一一对应;
（5）无限小数都是无理数；
（6）无理数都是无限小数。拓 展 拓 展 4、利用如图4×4方格，作出面积为8平方单位的正方形，然后在数轴上表示实数 和 拓 展 5、已知长方形的长与宽之比为3：2，面积为36m2，求长方形的长与宽