2.3 有理数的乘法(1) 课件(共22张PPT)
文档属性
| 名称 | 2.3 有理数的乘法(1) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-13 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
2.3 有理数的乘法(1)
浙教版七年级上册数学
有理数加减混合运算步骤:
(1) 利用减法法则,将减法统一为加法.
(2) 省略加号的和的形式,简化算式.
(3) 运用加法交换律、结合律,使运算简单.
=1+(-1)=0
温故知新:
-1-2-3-4-5
当前情况:
四个有理数的加减混合运算
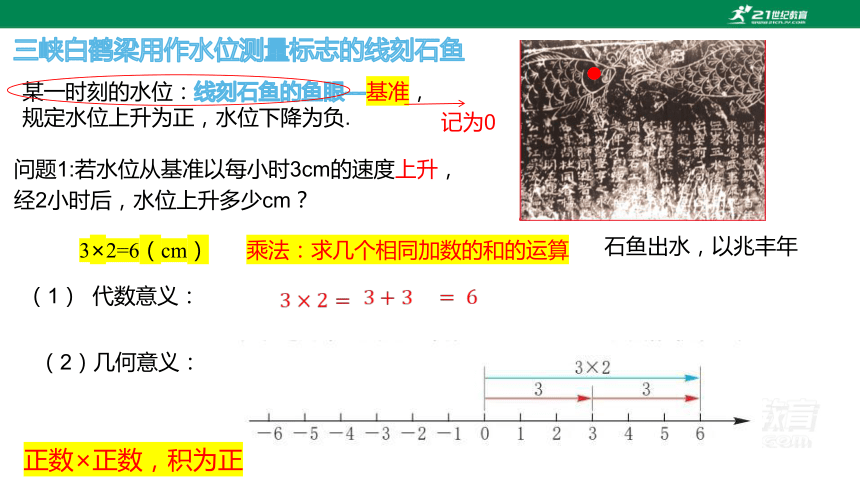
某一时刻的水位:线刻石鱼的鱼眼---基准,
规定水位上升为正,水位下降为负.
问题1:若水位从基准以每小时3cm的速度上升, 经2小时后,水位上升多少cm?
3×2=6(cm)
三峡白鹤梁用作水位测量标志的线刻石鱼
(1) 代数意义:
(2)几何意义:
正数×正数,积为正
乘法:求几个相同加数的和的运算
记为0
石鱼出水,以兆丰年
(1) 代数意义:
(2)几何意义:
问题2:若水位从基准以每小时3cm的速度下降,经2小时后,水位下降多少cm?
当前水位---------0
负数×正数,积为负
线刻石鱼的鱼眼
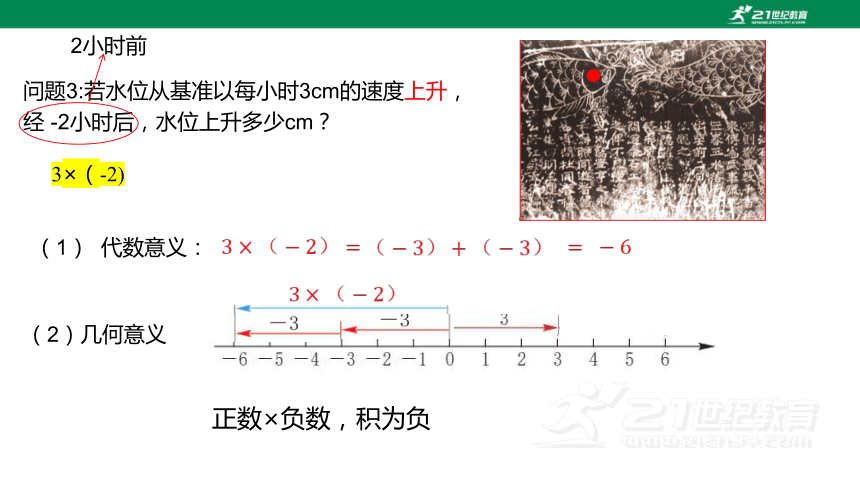
问题3:若水位从基准以每小时3cm的速度上升, 经 -2小时后,水位上升多少cm?
3×(-2)
(1) 代数意义:
(2)几何意义:
正数×负数,积为负
2小时前
(1) 代数意义:
(2)几何意义:
问题2:若水位从基准以每小时3cm的速度下降,经 -2小时后,水位下降多少cm?
负数×负数,积为正
当前水位---------0
线刻石鱼的鱼眼
①正数×正数,积为正
②负数×正数或正数×负数,积为负
③负数×负数,积为正
归纳:
正×正,负×负,叫做“同号相乘”
正×负,负×正,叫做“异号相乘”
有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与零相乘,积为零.
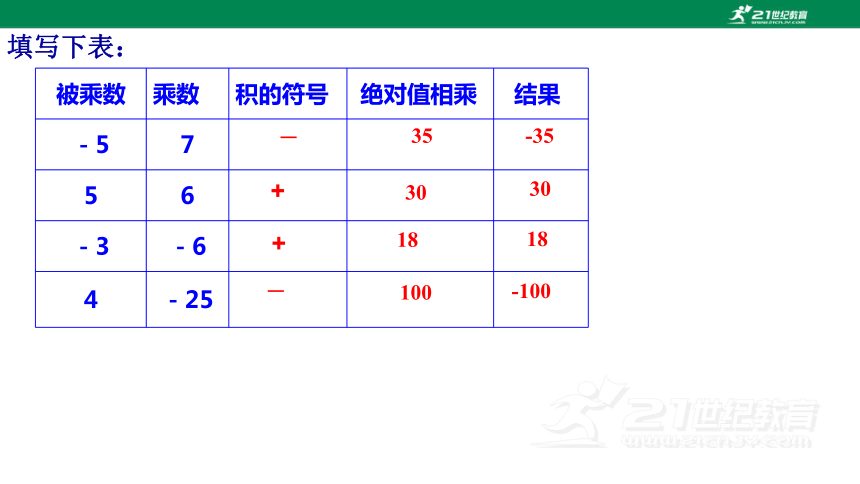
填写下表:
被乘数 乘数 积的符号 绝对值相乘 结果
-5 7
5 6
-3 -6
4 -25
—
35
-35
+
30
30
+
18
18
—
100
-100
例1、计算:
原式=-(2.5×4)=-10
原式=0
计算:
24
-24
24
24
-24
0
几个有理数相乘的时候,积的符号由什么决定?
负因数的个数
其中有一个乘数为0,积为0
注意:多个不为0的有理数相乘时,积的符号由负因数的个数决定,
当负因数的个数为奇数个时积为负,
当负因数的个数为偶数个时积为正,即:奇负偶正.
0乘以任何数都得0, 因此, 0没有倒数.
填一填:
2
?
若两个有理数的乘积为1,就称这两个有理数互为倒数。
-1 的倒数是: ;因为 ;
-1
(-1)×(-1)=1
-2 的倒数是: ;因为 ;
的倒数是: ;因为 ;
的倒数是: ;因为 ;
(-2)×( )=1
× =1
(- )×( - )=1
(2)说出下列各数的倒数
(1) -1 (2) -2 (3) (4) - 1
知识小结:
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。
2.如何进行两个有理数的运算:
先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。
3.如何进行多个有理数的运算:
先确定积的符号---------奇负偶正,再把绝对值相乘,当有一个因数为零时,积为零。
夯实基础,稳扎稳打
1.
<
>
=
<
2.计算
(1) (-6)×0.25 (2)(-0.5)×(-8)
(3) × ( ) (4) 2.9× (-0.4)
(5) (-0.3)×( ) (6)( ) × 25
解:(1)原式=-(6×0.25)=-1.5
(2)原式=+(0.5×8)=4
(4)原式=-(2.9×0.4)=-1.16
3.求下列各数的倒数
(3) 0.2的倒数是5;
(4)-0.25的倒数是 -4;
(6)1 的倒数是 1.
4、倒数等于它的本身的有理数有吗?是什么?
解:倒数等于它本身的有理数是±1.
-6=6
连续递推,豁然开朗
5. 把 -6 表示成两个整数的积,有多少种可能性?
把它们全部写出来
6.
-
-
+3
-
- 40
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.3 有理数的乘法(1)
浙教版七年级上册数学
有理数加减混合运算步骤:
(1) 利用减法法则,将减法统一为加法.
(2) 省略加号的和的形式,简化算式.
(3) 运用加法交换律、结合律,使运算简单.
=1+(-1)=0
温故知新:
-1-2-3-4-5
当前情况:
四个有理数的加减混合运算
某一时刻的水位:线刻石鱼的鱼眼---基准,
规定水位上升为正,水位下降为负.
问题1:若水位从基准以每小时3cm的速度上升, 经2小时后,水位上升多少cm?
3×2=6(cm)
三峡白鹤梁用作水位测量标志的线刻石鱼
(1) 代数意义:
(2)几何意义:
正数×正数,积为正
乘法:求几个相同加数的和的运算
记为0
石鱼出水,以兆丰年
(1) 代数意义:
(2)几何意义:
问题2:若水位从基准以每小时3cm的速度下降,经2小时后,水位下降多少cm?
当前水位---------0
负数×正数,积为负
线刻石鱼的鱼眼
问题3:若水位从基准以每小时3cm的速度上升, 经 -2小时后,水位上升多少cm?
3×(-2)
(1) 代数意义:
(2)几何意义:
正数×负数,积为负
2小时前
(1) 代数意义:
(2)几何意义:
问题2:若水位从基准以每小时3cm的速度下降,经 -2小时后,水位下降多少cm?
负数×负数,积为正
当前水位---------0
线刻石鱼的鱼眼
①正数×正数,积为正
②负数×正数或正数×负数,积为负
③负数×负数,积为正
归纳:
正×正,负×负,叫做“同号相乘”
正×负,负×正,叫做“异号相乘”
有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与零相乘,积为零.
填写下表:
被乘数 乘数 积的符号 绝对值相乘 结果
-5 7
5 6
-3 -6
4 -25
—
35
-35
+
30
30
+
18
18
—
100
-100
例1、计算:
原式=-(2.5×4)=-10
原式=0
计算:
24
-24
24
24
-24
0
几个有理数相乘的时候,积的符号由什么决定?
负因数的个数
其中有一个乘数为0,积为0
注意:多个不为0的有理数相乘时,积的符号由负因数的个数决定,
当负因数的个数为奇数个时积为负,
当负因数的个数为偶数个时积为正,即:奇负偶正.
0乘以任何数都得0, 因此, 0没有倒数.
填一填:
2
?
若两个有理数的乘积为1,就称这两个有理数互为倒数。
-1 的倒数是: ;因为 ;
-1
(-1)×(-1)=1
-2 的倒数是: ;因为 ;
的倒数是: ;因为 ;
的倒数是: ;因为 ;
(-2)×( )=1
× =1
(- )×( - )=1
(2)说出下列各数的倒数
(1) -1 (2) -2 (3) (4) - 1
知识小结:
1.有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘,任何数同0相乘,都得0。
2.如何进行两个有理数的运算:
先确定积的符号,再把绝对值相乘,当有一个因数为零时,积为零。
3.如何进行多个有理数的运算:
先确定积的符号---------奇负偶正,再把绝对值相乘,当有一个因数为零时,积为零。
夯实基础,稳扎稳打
1.
<
>
=
<
2.计算
(1) (-6)×0.25 (2)(-0.5)×(-8)
(3) × ( ) (4) 2.9× (-0.4)
(5) (-0.3)×( ) (6)( ) × 25
解:(1)原式=-(6×0.25)=-1.5
(2)原式=+(0.5×8)=4
(4)原式=-(2.9×0.4)=-1.16
3.求下列各数的倒数
(3) 0.2的倒数是5;
(4)-0.25的倒数是 -4;
(6)1 的倒数是 1.
4、倒数等于它的本身的有理数有吗?是什么?
解:倒数等于它本身的有理数是±1.
-6=6
连续递推,豁然开朗
5. 把 -6 表示成两个整数的积,有多少种可能性?
把它们全部写出来
6.
-
-
+3
-
- 40
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
