浙教版八上数学第一章 三角形的初步知识 单元练习卷(含答案)
文档属性
| 名称 | 浙教版八上数学第一章 三角形的初步知识 单元练习卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 377.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 16:19:01 | ||
图片预览




文档简介
浙教版八上数学第一章
一、单选题
1.下列生活实例中,利用了“三角形稳定性”的是( )
A. B.
C. D.
2.如图,△ABC≌△EBD,AB=4cm,BD=7cm,则CE的长度为( )
A.1cm B.2cm C.3cm D.4cm
3.如图,在中,,是角平分线,于点E,,,则( )
A.2 B. C. D.6
4.如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
作法:
①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E;
②分别以D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB内交于一点C;
③画射线OC,射线OC就是∠AOB的角平分线.
A.ASA B.SAS C.SSS D.AAS
5.如图,将绕点逆时针旋转一定的角度,得到,且.若,,则的大小是( )
A. B. C. D.
6.如图,已知锐角∠AOB,根据以下要求作图.
(1)在射线OA上取点C和点E,以点O为圆心,OC,OE的长为半径画弧,分别交射线OB于点D,F;
(2)连接CF,DE交于点P.
则下列结论错误的是( )
A.CE=DF
B.点P在∠AOB的平分线上
C.PE=PF
D.若∠AOB=60°,则∠CPD=120°
7.三边长度都是整数的三角形称为整数边三角形,若一个三角形的最长边长为8,则满足条件的整数边三角形共有( )
A.8个 B.10个 C.12个 D.20个
8.如图所示,在△ABC中,点O是∠BCA与∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离OD是( )
A.1 B.2 C.3 D.4
9.如右图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=129°,则∠2的度数为( )
A.49° B.50° C.51° D.52°
10.如图,点 是 的中点,平分 ,下列结论:①;②;③;④,四个结论中成立的是( )
A.①②④ B.①②③ C.③④ D.①③
二、填空题
11.已知三角形的三边长分别是2、7、,且为奇数,则 .
12.“两直线平行,同位角相等”是 命题(真、假).
13.如图,在中,,如果与的平分线交于点D,那么 度.
14.在中,平分,如果,,的面积为24,则的面积为
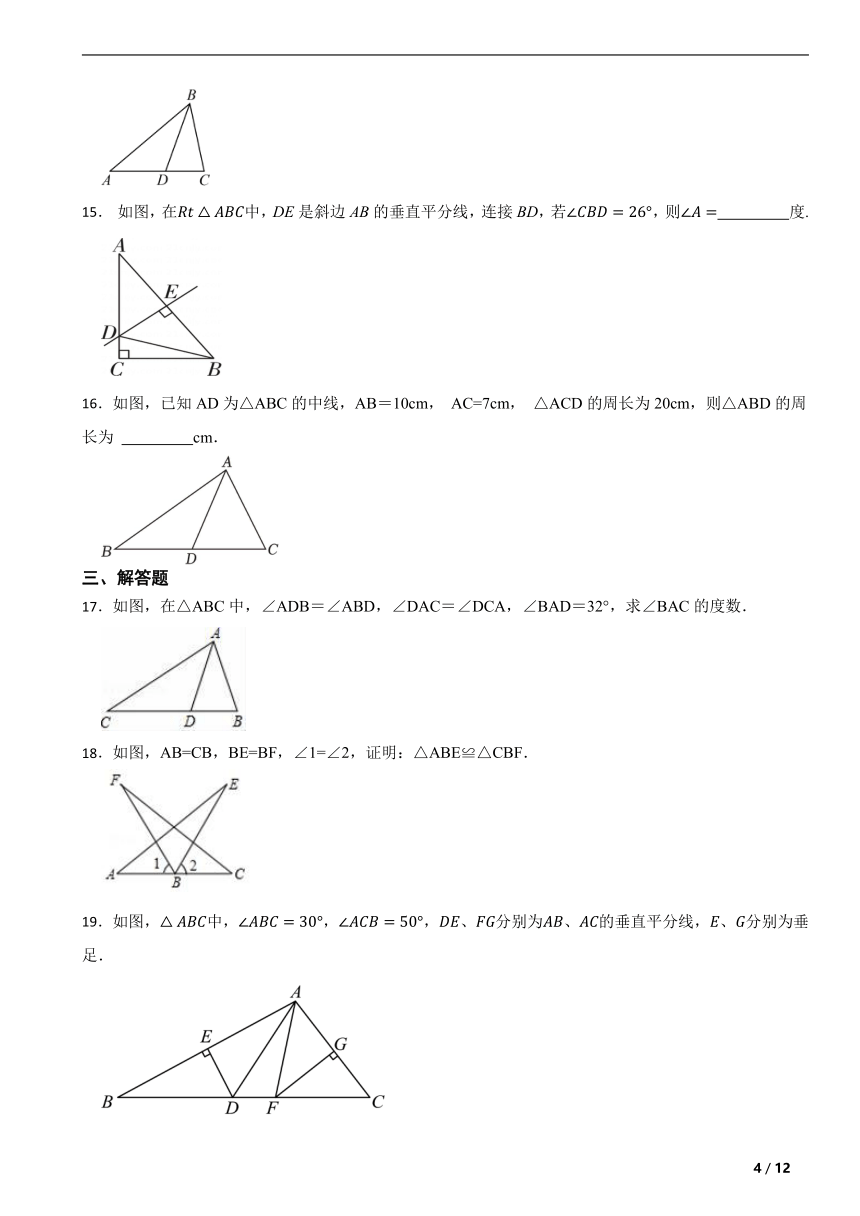
15. 如图,在中,DE是斜边AB的垂直平分线,连接BD,若,则 度.
16.如图,已知AD为△ABC的中线,AB=10cm, AC=7cm, △ACD的周长为20cm,则△ABD的周长为 cm.
三、解答题
17.如图,在△ABC中,∠ADB=∠ABD,∠DAC=∠DCA,∠BAD=32°,求∠BAC的度数.
18.如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
19.如图,中,,,、分别为、的垂直平分线,、分别为垂足.
(1)的度数为______,的度数为______;
(2)若的周长为,求的长.
20.如图,已知在中,,,D为的中点.点P在线段上以的速度由点B出发向终点C运动,同时点Q在线段上以的速度由点C出发向终点A运动,设点P的运动时间为.
(1)求的长;(用含的式子表示)
(2)若以为顶点的三角形和以为顶点的三角形全等,且和是对应角,求的值.
21.定义: 在一个三角形中, 如果有一个角是另一个角的, 我们称这两个角互为 “和谐角”, 这个三角形叫做 “和谐三角形” .
例如: 在 中, 如果, 那么 与 互为 “和谐角”, 为 “和谐三角形”.
问题 1: 如图 1, 中,, 点 是线段 A BB 上一点(不与 A、B 重合),连接CD
(1)如图 1,△ABC 是“和谐三角形”吗?为什么?
(2)如图 1, 若, 则 是 “和谐三角形” 吗? 为什么?
(3)问题 2:如图 2,△ABC 中,∠ACB=60°,∠A=80°,点 D 是线段 AB 上一点(不与 A、B 重合),连接 CD,若△ACD 是“和谐三角形”,求∠ACD 的度数.
22.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
23.
(1)阅读理解:问题:如图1,在四边形 中,对角线 平分 , .求证: .
思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在 上截取 ,连接 ,得到全等三角形,进而解决问题;
方法2:延长 到点N,使得 ,连接 ,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种,添加辅助线并完成证明.
(2)问题解决:如图2,在(1)的条件下,连接 ,当 时,探究线段 , , 之间的数量关系,并说明理由;
(3)问题拓展:如图3,在四边形 中, , ,过点D作 ,垂足为点E,请直接写出线段 、 、 之间的数量关系.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】7
12.【答案】真
13.【答案】
14.【答案】16
15.【答案】32
16.【答案】23
17.【答案】解 :在三角形ABD中,
∠ADB=∠ABD= (180°﹣32°)=74°,
在三角形ADC中,
∠DAC=∠DCA= ∠ADB=37°,
∴∠BAC=∠DAC+∠BAD=37°+32°=69°.
18.【答案】证明:∵∠1=∠2,
∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF
在△ABE与△CBF中,
∴△ABE≌△CBF(SAS).
19.【答案】(1),;
(2).
20.【答案】(1)
(2)或
21.【答案】(1)解:是“和谐三角形”,理由如下:
,,
,
,
是“和谐三角形”;
(2)解:、是“和谐三角形”,理由如下:
,,
,
,
,
,.
在中,
,,
,
为和谐三角形”;
在中,
,,
,
为和谐三角形”;
(3)解:若是“和谐三角形”,由于点是线段上一点(不与、重合),
则或.
当时,;
当时,,即,
.
综上,的度数为或.
22.【答案】(1)解:如图,∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°
(2)解:∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°
(3)解:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180×5+180=1080°.
23.【答案】(1)解:方法1:在 上截 ,连接 ,如图.
平分 ,
.
在 和 中, ,
,
, .
, .
.
,
.
方法2:延长 到点N,使得 ,连接 ,如图.
平分 ,
.
在 和 中, ,
.
, .
,
.
,
,
.
(2)解: 、 、 之间的数量关系为: .
(或者: , ).
延长 到点P,使 ,连接 ,如图2所示.
由(1)可知 ,
.
为等边三角形.
, .
,
.
.
,
为等边三角形.
, .
,
,
即 .
在 和 中, ,
.
,
,
.
(3)
1 / 1
一、单选题
1.下列生活实例中,利用了“三角形稳定性”的是( )
A. B.
C. D.
2.如图,△ABC≌△EBD,AB=4cm,BD=7cm,则CE的长度为( )
A.1cm B.2cm C.3cm D.4cm
3.如图,在中,,是角平分线,于点E,,,则( )
A.2 B. C. D.6
4.如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )
作法:
①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E;
②分别以D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB内交于一点C;
③画射线OC,射线OC就是∠AOB的角平分线.
A.ASA B.SAS C.SSS D.AAS
5.如图,将绕点逆时针旋转一定的角度,得到,且.若,,则的大小是( )
A. B. C. D.
6.如图,已知锐角∠AOB,根据以下要求作图.
(1)在射线OA上取点C和点E,以点O为圆心,OC,OE的长为半径画弧,分别交射线OB于点D,F;
(2)连接CF,DE交于点P.
则下列结论错误的是( )
A.CE=DF
B.点P在∠AOB的平分线上
C.PE=PF
D.若∠AOB=60°,则∠CPD=120°
7.三边长度都是整数的三角形称为整数边三角形,若一个三角形的最长边长为8,则满足条件的整数边三角形共有( )
A.8个 B.10个 C.12个 D.20个
8.如图所示,在△ABC中,点O是∠BCA与∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离OD是( )
A.1 B.2 C.3 D.4
9.如右图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=129°,则∠2的度数为( )
A.49° B.50° C.51° D.52°
10.如图,点 是 的中点,平分 ,下列结论:①;②;③;④,四个结论中成立的是( )
A.①②④ B.①②③ C.③④ D.①③
二、填空题
11.已知三角形的三边长分别是2、7、,且为奇数,则 .
12.“两直线平行,同位角相等”是 命题(真、假).
13.如图,在中,,如果与的平分线交于点D,那么 度.
14.在中,平分,如果,,的面积为24,则的面积为
15. 如图,在中,DE是斜边AB的垂直平分线,连接BD,若,则 度.
16.如图,已知AD为△ABC的中线,AB=10cm, AC=7cm, △ACD的周长为20cm,则△ABD的周长为 cm.
三、解答题
17.如图,在△ABC中,∠ADB=∠ABD,∠DAC=∠DCA,∠BAD=32°,求∠BAC的度数.
18.如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
19.如图,中,,,、分别为、的垂直平分线,、分别为垂足.
(1)的度数为______,的度数为______;
(2)若的周长为,求的长.
20.如图,已知在中,,,D为的中点.点P在线段上以的速度由点B出发向终点C运动,同时点Q在线段上以的速度由点C出发向终点A运动,设点P的运动时间为.
(1)求的长;(用含的式子表示)
(2)若以为顶点的三角形和以为顶点的三角形全等,且和是对应角,求的值.
21.定义: 在一个三角形中, 如果有一个角是另一个角的, 我们称这两个角互为 “和谐角”, 这个三角形叫做 “和谐三角形” .
例如: 在 中, 如果, 那么 与 互为 “和谐角”, 为 “和谐三角形”.
问题 1: 如图 1, 中,, 点 是线段 A BB 上一点(不与 A、B 重合),连接CD
(1)如图 1,△ABC 是“和谐三角形”吗?为什么?
(2)如图 1, 若, 则 是 “和谐三角形” 吗? 为什么?
(3)问题 2:如图 2,△ABC 中,∠ACB=60°,∠A=80°,点 D 是线段 AB 上一点(不与 A、B 重合),连接 CD,若△ACD 是“和谐三角形”,求∠ACD 的度数.
22.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
23.
(1)阅读理解:问题:如图1,在四边形 中,对角线 平分 , .求证: .
思考:“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1:在 上截取 ,连接 ,得到全等三角形,进而解决问题;
方法2:延长 到点N,使得 ,连接 ,得到全等三角形,进而解决问题.
结合图1,在方法1和方法2中任选一种,添加辅助线并完成证明.
(2)问题解决:如图2,在(1)的条件下,连接 ,当 时,探究线段 , , 之间的数量关系,并说明理由;
(3)问题拓展:如图3,在四边形 中, , ,过点D作 ,垂足为点E,请直接写出线段 、 、 之间的数量关系.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】7
12.【答案】真
13.【答案】
14.【答案】16
15.【答案】32
16.【答案】23
17.【答案】解 :在三角形ABD中,
∠ADB=∠ABD= (180°﹣32°)=74°,
在三角形ADC中,
∠DAC=∠DCA= ∠ADB=37°,
∴∠BAC=∠DAC+∠BAD=37°+32°=69°.
18.【答案】证明:∵∠1=∠2,
∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF
在△ABE与△CBF中,
∴△ABE≌△CBF(SAS).
19.【答案】(1),;
(2).
20.【答案】(1)
(2)或
21.【答案】(1)解:是“和谐三角形”,理由如下:
,,
,
,
是“和谐三角形”;
(2)解:、是“和谐三角形”,理由如下:
,,
,
,
,
,.
在中,
,,
,
为和谐三角形”;
在中,
,,
,
为和谐三角形”;
(3)解:若是“和谐三角形”,由于点是线段上一点(不与、重合),
则或.
当时,;
当时,,即,
.
综上,的度数为或.
22.【答案】(1)解:如图,∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°
(2)解:∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°
(3)解:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180×5+180=1080°.
23.【答案】(1)解:方法1:在 上截 ,连接 ,如图.
平分 ,
.
在 和 中, ,
,
, .
, .
.
,
.
方法2:延长 到点N,使得 ,连接 ,如图.
平分 ,
.
在 和 中, ,
.
, .
,
.
,
,
.
(2)解: 、 、 之间的数量关系为: .
(或者: , ).
延长 到点P,使 ,连接 ,如图2所示.
由(1)可知 ,
.
为等边三角形.
, .
,
.
.
,
为等边三角形.
, .
,
,
即 .
在 和 中, ,
.
,
,
.
(3)
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
