2.1直线与圆的位置关系（1）课件

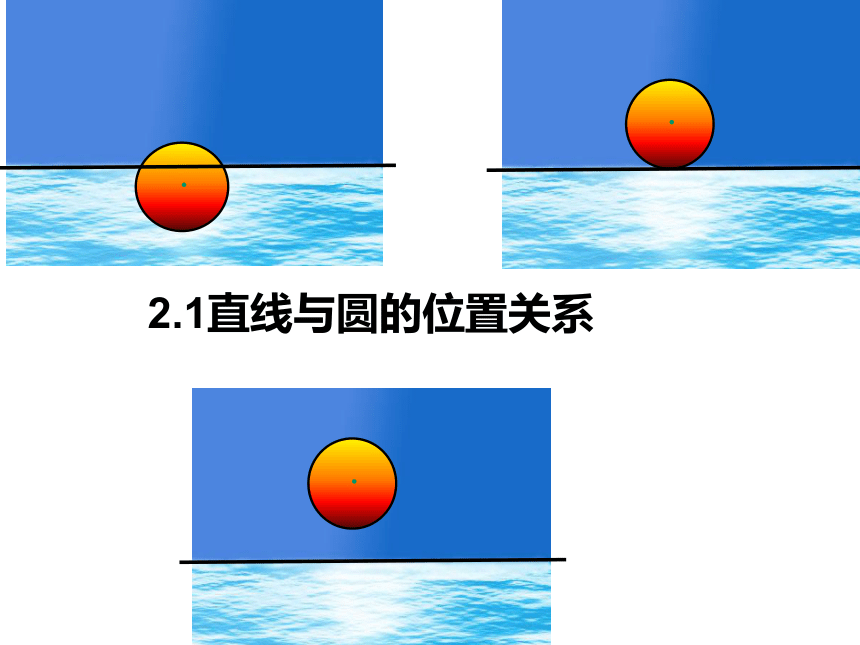
课件23张PPT。2.1直线与圆的位置关系3）直线和圆没有公共点时，叫做直线和圆相离.lll直线与圆的位置关系： 2）直线和圆有唯一公共点时，叫做直线和圆相切； 1）直线和圆有两个公共点时，叫做直线和圆相交；定义： 这时直线叫做圆的切线,，唯一的公共点叫做切点;这时直线叫做圆的割线。相交相切相离直线与圆的位置关系有 种.
3没有公共点相离有唯一公共点相切切点切线有两个公共点相交割线（由公共点的个数判定）生活中的数学你还能举出生活中直线和圆的位置关系的例子吗？说明学生举例说明生活中的三种直线与圆的位置关系
生活中找数学×.A1.若A为⊙O上的一点，则过点A的直线与⊙O相切( )判一判 2.若A、B是⊙O外两点， 则直线AB与⊙O相离。( )×.B1.
B2判一判看图判断直线l与 ⊙O的位置关系（1）（2）（3）（4）（5）相离相切相交相交lllll·O·O·O·O·O看一看有唯一公共点（5）？l 如果，公共点的个数不好判断，该怎么办？·O探究：还有没有其它方法判定直线与圆的位置关系呢？d r; 直线和圆相交 直线和圆相切 直线和圆相离d r;<=>d r;直线与圆的位置关系比一比d表示圆心O到直线l的距离， r表示⊙O的半径数量关系图形位置关系转化判定直线与圆的位置关系的方法有____种：（1）由________________ 的个数来判断；（2）由___________________________ 的
数量大小关系来判断．两直线与圆的公共点圆心到直线的距离d与半径r
CD= = =2.4(cm)
AB= 　= =5即 圆心C到AB的距离d=2.4cm
解：过C作CD⊥AB，垂足为D，则 　　在△ABC中,∠C=900 , AC=3cm，　BC=4cm，设⊙C的半径为r，请根据r的下列值，
判断直线AB与⊙C的位置关系，并说明理由。(1) r=2cm;(2) r=2．4cm(3) r=3cm 在Rt△ABC中，根据三角形的面积公式有例1(1) r = 2（2）r =2.4（３）r =３当r =2cm时，

当r =2.4cm时，
d = r，
∴☉C 与直线AB相切； 当r =3cm时，
d < r，
∴☉C 与直线AB相交。d > r，∴☉C 与直线
AB相离；在Rt△ABC中，∠C=90°，AC=3cm，
BC=4cm，以C为圆心，r为半径作圆。1．当r满足________________时，⊙C与直线AB相离。2．当r满足____________ 时，⊙C与直线AB相切。3．当r满足____________时，
⊙C与直线AB相交。BCAD4530cm则⊙A与X轴的位置关系是_____,⊙A与Y轴的
位置关系是______。BC43相离相切 如图：菱形ABCD的边长为5cm，∠B=60°
当以A为圆心的圆与BC相切时，半径是 ，
此时⊙A与CD的位置关系是 。思考题：练 习 （一）填空：1、已知⊙O的半径为5cm，O到直线a的距离为3cm，则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm，O到直线a的距离是4cm，则⊙O与直线a的位置关系是 ___ 。相交 相切两个
3、已知⊙O的半径为6cm，O到
直线a的距离为7cm，则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm，
O到直线a的距离是4cm，
则⊙O与直线a的位置关系是 ___ _。零相离直线与圆的位置关系2 个交点割线1 个切点切线d < rd = rd > r没有理一理