3.1 圆(2)

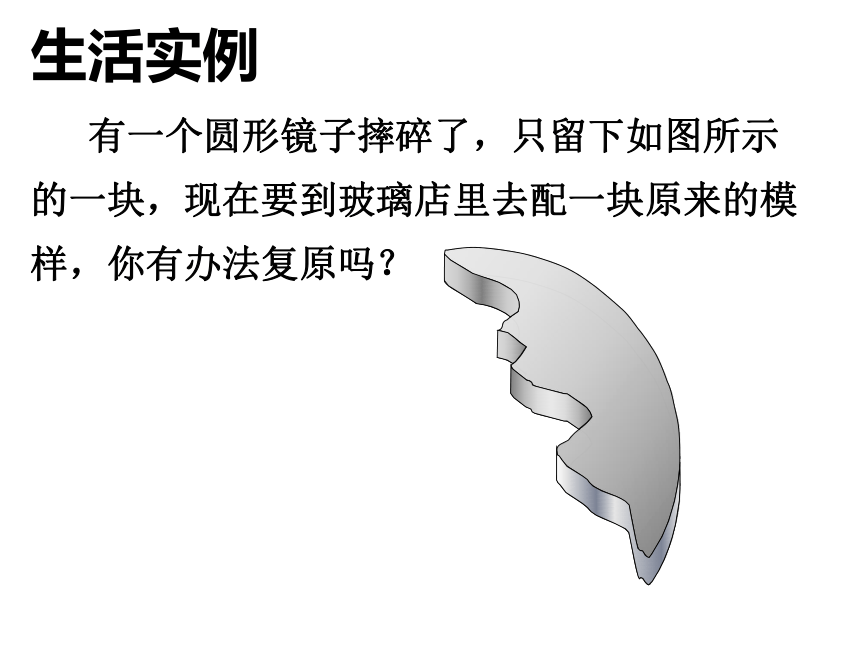
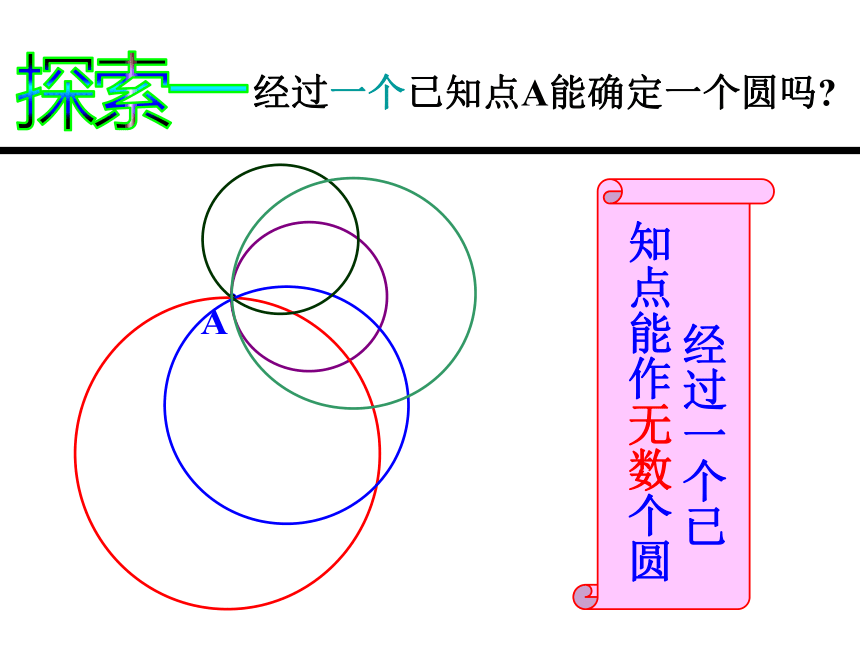
课件24张PPT。3.1 圆（2）九年级备课组 有一个圆形镜子摔碎了，只留下如图所示的一块，现在要到玻璃店里去配一块原来的模样，你有办法复原吗？生活实例1、过一点可以作几条直线？2、过几点确定一条直线？过几点可以确定一个圆？合作探索两点确定一条直线 在平面上任意取一个点A,以这个点A为圆心画圆,画出的圆的大小一样吗?共同探究以3cm为半径画圆,画出的圆位置确定吗? 只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.探索一经过一个已知点A能确定一个圆吗?A 经过一个已知点能作无数个圆
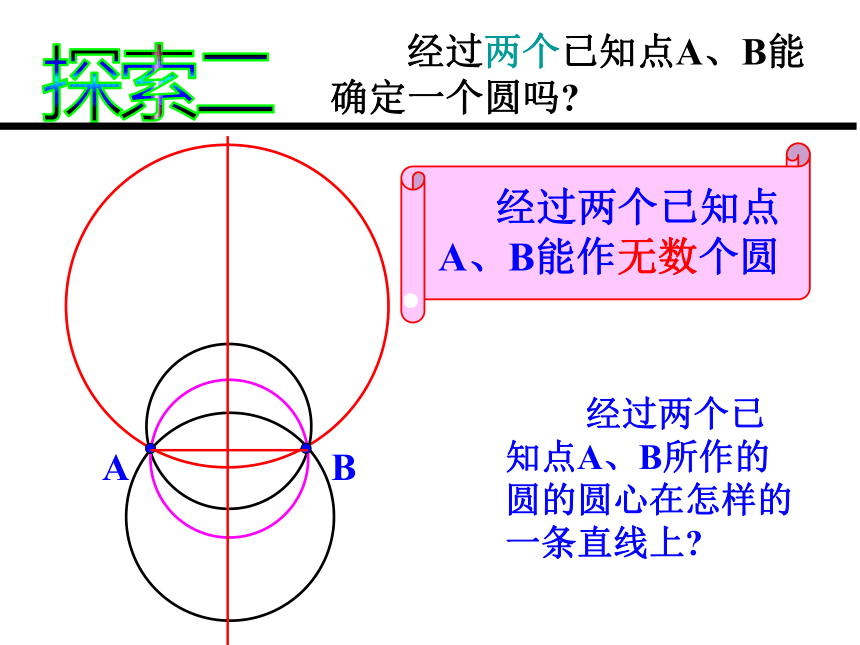
探索二 经过两个已知点A、B能确定一个圆吗?AB 经过两个已知点A、B能作无数个圆 经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
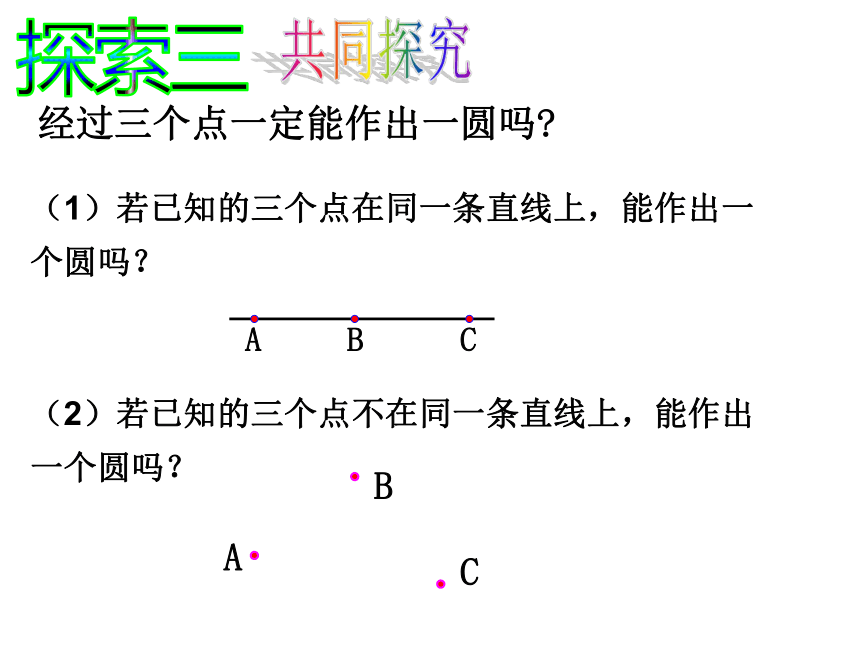
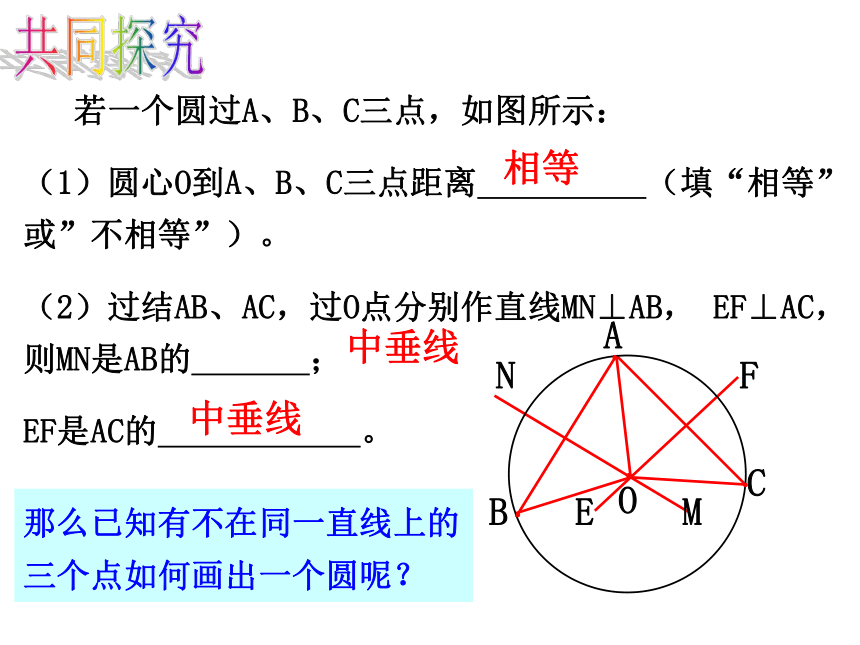
经过三个点一定能作出一圆吗?共同探究（1）若已知的三个点在同一条直线上，能作出一个圆吗？（2）若已知的三个点不在同一条直线上，能作出一个圆吗？探索三 若一个圆过A、B、C三点，如图所示：
（1）圆心O到A、B、C三点距离 （填“相等”或”不相等”）。
（2）过结AB、AC，过O点分别作直线MN⊥AB， EF⊥AC，则MN是AB的 ；
EF是AC的 。ONMFE共同探究相等中垂线中垂线那么已知有不在同一直线上的三个点如何画出一个圆呢？画一画作法：1、连结AB，作线段AB 的垂直平分 线MN；
2、连接AC，作线段AC的垂直平分 线EF，交MN于点O；
3、以O为圆心，OB为半径作圆。
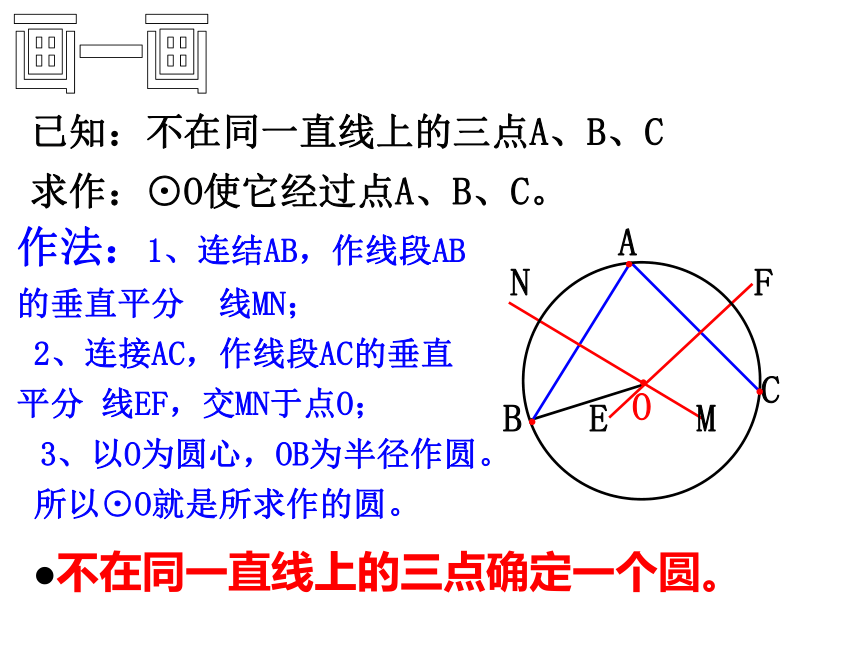
所以⊙O就是所求作的圆。已知：不在同一直线上的三点A、B、C
求作：⊙O使它经过点A、B、C。ONMFEABC不在同一直线上的三点确定一个圆。已知△ABC,用直尺和圆规作出过点A,B,C的圆.CBAO练一练定义:C 经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心外心是△ABC三条边的垂直平分线的交点.O练一练如图,请找出图中圆的圆心,并写出你找圆心的方法? 现在你知道了怎样要将一个如图所示的破损的圆盘复原了吗？方法:
寻求圆弧所在圆的圆心,在圆弧上任取三点,作其连线段的垂直平分线,其交点即为圆心.试一试分别画锐角三角形，直角三角形，
钝角三角形的外接圆并观察外心的位置；
●OCAB┐●O●O思 考图二中，若AB=3，BC=4，则它的外接圆半径是多少？（图一）（图二）（图三）外心在三角形的内部外心在三角形的斜边上外心在三角形的外部1.下列命题不正确的是（ ）
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能画圆.CB练一练2.三角形的外心具有的性质是（ ）
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.3、已知直角三角形的两条直角边长是6cm和8cm,则这个三角形的外接圆的半径是______cm.5圆上4、如图, ∠ABC=∠ADC=900.若△ABC的外接圆为⊙O,则点D与⊙O的位置是:点在______.练一练探究活动一植物园动物园人工湖１．某市要建一个圆形公园，要求公园刚好把动物园A，植物园B和人工湖C包括在内，又要使这个圆形的面积最小，请你给出这个公园的施工图。（A、B、C不在同一直线上）谈收获:(1)只有确定了圆心和圆的半径,这个圆的位置和大小才
唯一确定.(2)经过一个已知点能作无数个圆!(3)经过两个已知点A,B能作无数个圆!这些圆的圆心在线段AB的中垂线上.(4)不在同一直线上的三个点确定一个圆.(5)外接圆,外心的概念.２．设计师通常用“T”字尺（如图，AB恰好被CD所在的直线垂直平分）来找已知圆的圆心，你知道他是怎样找的吗？谈谈你的想法.
·圆心探究活动二·圆心已知圆上两点A,B，用直尺和圆规求作
以AB为边的圆内接等腰三角形。
这样的三角形有几个？●●AB分类讨论探究活动谈收获:（2）经过一点能作无数个圆！
经过两个已知点A、B能作无数个圆！
圆心在线段AB的垂直平分线上
不在同一直线上的三个点确定一个圆。
同一直线上的三个点 不能画圆（5）外接圆，外心的概念。6、平面上有4个点,它们不在一条直线上,但有3个点在同一条直线上,问过其中3个点作圆,可以作出几个圆?请说明理由,并作出图形.ABCD练一练再见