2024年浙江省舟山市定海区定海二中九年级上册数学第一章二次函数质量监测试题卷(含答案)
文档属性
| 名称 | 2024年浙江省舟山市定海区定海二中九年级上册数学第一章二次函数质量监测试题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 14:08:27 | ||
图片预览




文档简介
保密★启用前
2024年定海二中九年级上数学第一章二次函数质量监测
1.全卷共三大题,24小题,共8页。满分120分,考试时间120分钟。
2.全卷分卷I(选择题)和卷II(非选择题)两部分,全部在答题纸上作答。卷I的答案必须用2B铅笔填涂;卷II的答案必须用黑色钢笔或签字笔写在答题纸相应位置上。
3.考试时不能使用计算器。
第I卷(选择题)
选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.下列函数一定是二次函数的是( )
A. B.
C. D.
2.若是二次函数,则( )
A.7 B. C.或7 D.以上都不对
3.若二次函数的图象经过点,则该图象必经过点( )
A. B. C. D.
4.关于抛物线,下列说法中错误的是( )
A.开口方向向上 B.对称轴是直线
C.当时,y随x的增大而增大 D.顶点坐标为
5.在同一平面直角坐标系中,一次函数和二次函数的大致图象是( )
A. B.
C. D.
6.若抛物线与x轴有两个交点,则k的取值范围为( )
A. B. C.且 D.且
7.如图,正方形的边长为4cm,动点P、Q同时从点A出发,以的速度分别沿和的路径向点C运动,设运动时间为x(单位:s),四边形的面积为y(单位:cm2),则y与x()之间函数关系可以用图象表示为( )
A. B. C. D.
8.在平面直角坐标系中,直线与抛物线相交于,,且,则下列说法正确的是( )
A.若,m有最大值 B.若,m有最小值
C.若,m有最大值 D.若,m有最小值
9.已知二次函数,当时,随的增大而增大,则实数的取值范围是( )
A. B. C. D.
10.对于二次函数,规定函数是它的相关函数.已知点M,N的坐标分别为,,连接,若线段与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )
A.或 B.或
C.或 D.或
第II卷(非选择题)
二、填空题(本题有6小题,每题4分,共24分)
11.已知函数 是二次函数,那么 .
12.已知关于的二次函数,当时,的取值范围为
13.抛物线经过点,,以及点D,若点D的横坐标为,则点D的纵坐标是 (用n的式子含表示).
14.二次函数的最小值是 .
15.如图,抛物线与x轴交于点A、B(点A在B左侧),抛物线的顶点为C,点 D为抛物线上一点,且在对称轴右侧,若的面积为3,则点D的坐标为 .
16.如图(示意图),某跳水运动员进行10m跳台跳水训练,水面边缘点E的坐标为.运动员(将运动员看成一点)在空中运动的路线是经过原点O的抛物线.运动员在空中最高处点A的坐标为运动员入水后,运动路线为另一条抛物线,在该运动员入水点的正前方有M,N两点,且,该运动员入水后运动路线对应的抛物线的函数解析式为,且顶点C距水面5m,若该运动员出水点D在MN之间(包括M,N两点),则a的取值范围 .
解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.已知
(1)化简T.
(2)若a为二次函数的最小值,求此时的T值.
18.已知二次函数中,函数y与自变量x的部分对应值如下表:
0 2
5
(1)求二次函数的解析式;
(2)求该函数图象与x轴的交点坐标;
19.已知二次函数的顶点坐标是.
(1)当时,求该二次函数的表达式;
(2)在(1)的条件下,当时,求该二次函数的最大值
20.某游乐园有一个直径为米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心米处达到最高,高度为米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为 轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式.
(2)游乐园决定对喷水设施做如下设计改进,在喷出水柱的形状不变的前提下,把水池的直径扩大到 米,各方面喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合.请求出扩建改造后喷水池水柱的最大高度?
21.已知抛物线经过.
(1)求抛物线的表达式及对称轴;
(2)若是抛物线上不同的两点,且,求n的值;
(3)将抛物线沿x轴向左平移m()个单位长度,当时,它的函数值y的最小值为7,求m的值.
22.阅读与思考
下面是小明在数学笔记本上记录的父亲工厂里实际出现过的一个问题,请认真阅读,并帮助小明解答小明父亲给的以下任务:
小明父亲的工厂里加工一款纪念品,每件成本为元,投放景区内进行销售,售价不得低于成本价且利润率不高于,销售一段时间后市场调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:
销售单价x(元/件) … …
每天销售数量y(件) … …
(1)直接写出y与x的函数关系式;
(2)当销售单价为多少元时,每天获利最大?最大利润是多少元?
(3)若每天销售所得利润为元,那么销售单价应定为多少元?
任务一:要解决小明父亲提出的问题,主要运用的数学思想是________;
A.公理化思想 B.统计思想 C.函数思想 D.分类思想
任务二:请帮助小明解决相关的3个问题.
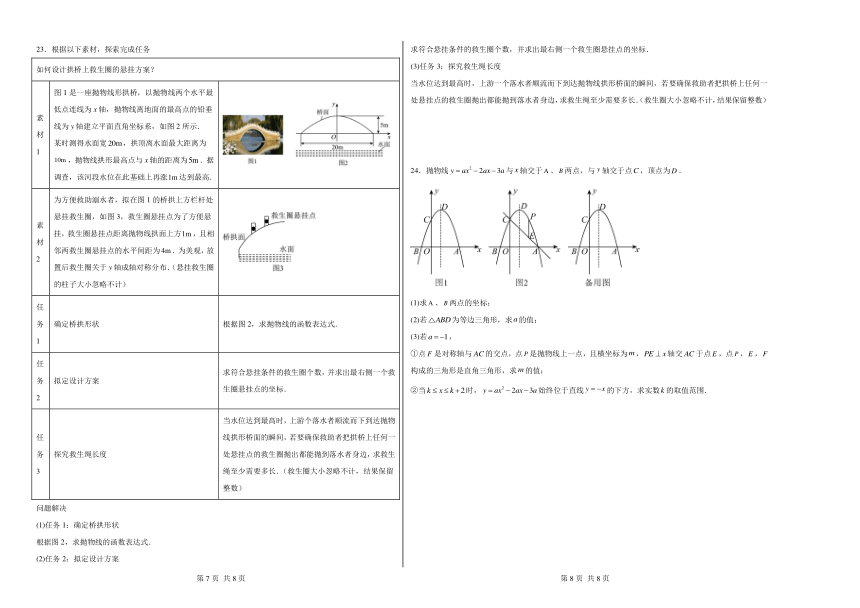
23.根据以下素材,探索完成任务
如何设计拱桥上救生圈的悬挂方案?
素材1 图1是一座抛物线形拱桥,以抛物线两个水平最低点连线为x轴,抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系,如图2所示. 某时测得水面宽,拱顶离水面最大距离为,抛物线拱形最高点与x轴的距离为.据调查,该河段水位在此基础上再涨达到最高.
素材2 为方便救助溺水者,拟在图1的桥拱上方栏杆处悬挂救生圈,如图3,救生圈悬挂点为了方便悬挂,救生圈悬挂点距离抛物线拱面上方,且相邻两救生圈悬挂点的水平间距为.为美观,放置后救生圈关于y轴成轴对称分布.(悬挂救生圈的柱子大小忽略不计)
任务1 确定桥拱形状 根据图2,求抛物线的函数表达式.
任务2 拟定设计方案 求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
任务3 探究救生绳长度 当水位达到最高时,上游个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
问题解决
(1)任务1:确定桥拱形状
根据图2,求抛物线的函数表达式.
(2)任务2:拟定设计方案
求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
(3)任务3:探究救生绳长度
当水位达到最高时,上游一个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
24.抛物线与轴交于、两点,与轴交于点,顶点为.
(1)求、两点的坐标;
(2)若为等边三角形,求的值;
(3)若,
①点是对称轴与的交点,点是抛物线上一点,且横坐标为,轴交于点,点,,构成的三角形是直角三角形,求的值;
②当时,始终位于直线的下方,求实数的取值范围.
第1页 共4页 第2页 共4页
第1页 共4页 第2页 共4页
参考答案:
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B B B C B D D B
二、填空题(本题有6小题,共24分)
11. 12. 13.
14. 15. 16.
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(1)
,
∴.
(2),
∴二次函数的最小值为3,即,
∴.
18.解:(1)由题意,当
∴得.
将点,代入,
得,
解得,二次函数的解析式为;
(2)当时,,
解得:或,
该函数图象与轴的交点坐标,;
19.解:(1)根据题意可得,二次函数的顶点坐标是.
∴对称轴,
∵
∴,
∴二次函数的表达式为.
(2)如图,∵二次函数的表达式为,
∴当时,y的值随x值得增大而增大,
∵,
∴当时,y的值随x值得增大而增大,
∴当时,二次函数有最大值,
解得.
20.解(1)由喷出的水柱为抛物线,在距水池中心4米处达到最高,高度为6米,设水柱所在抛物线(第一象限部分)的函数表达式为,
将代入,得:,
解得:,
∴水柱所在抛物线(第一象限部分)的函数表达式为.
(2)当时, .
设改造后水柱所在抛物线(第一象限部分)的函数表达式为.
∵该函数图象过点,
∴,
解得:,
∴改造后水柱所在抛物线(第一象限部分)的函数表达式为,
∵
∴扩建改造后喷水池水柱的最大高度为米.
21.解(1)把点代入得,
,
解得:;
∴函数解析式为,
∴对称轴为
(2)由(1)得函数解析式为,
把代入得,,
∵
∴
∵是抛物线上不同的两点,
∴关于对称轴的对称,
∴.
∴.
(3)由(1)得函数解析式为,
∵此抛物线沿x轴向左平移m()个单位长度,
当向左平移时,平移后的解析式为,
∴对称轴为,
当时,顶点处取最小值,此时最小值为,不合题意;
当,时,当时y随x的增大而增大,
∴当时,有最小值7,即,
解得,(舍去),
综上所述,m的值为5.
22.解:任务一:由题意可得,
主要运用函数的数学思想,
故选:C;
任务二:(1)设,将,代入得,
,解得:,
∴,
∵售价不得低于成本价且利润率不高于,
∴,解得:,
∴;
(2)设利润为w,由题意可得,
∵,,
∴随增大而增大,
∴当时最大,
∴,
∴当销售单价为元时,每天获利最大,最大利润是元;
(3)当时,
,
解得:,(不符合题意舍去),
∴若每天销售所得利润为元,那么销售单价应定为元;
23.解(1)如图,知抛物线关于y轴对称,设解析式为,抛物线经过,,得,解得
∴.
(2)在,当,,解得或,
∴点
如题,相邻两救生圈悬挂点的水平间距为,且关于y轴成轴对称,
∵
∴左侧可挂3个,
由对称性只看右面,右面可挂3个,则此时最中间的两个救生圈的水平距离为,符合题意,
∴桥面一共可以挂6个救生圈,最右侧位于点上方处,即该点的坐标为.
(3)如图,当水位达到最高时,水位线为,
救生圈悬挂点距离抛物线拱面上方,当时,,,,
中,,
∴绳长至少需.
24.解(1)令,即,
∵,
∴,解得:,,
∴,;
(2)由,
∴,
由()得:,,
∴,,,
∵是等边三角形,
∴,
∴,解得:,
根据图象可知:,
∴;
(3)当时,,
令,则,
∴,
∴,
∴,
设直线解析式为,
∴,解得:,
∴解析式为,
∴当时,,
∴,
如图,当时,
∵,即轴,
∴,
∴,
∵的横坐标为,,
∴,,
∴,,
∴或,
整理得:或,
解得:(舍去)或,
如图,当时,
由上可知,,
由勾股定理得:,
∴,
∴或,
解得:(舍去)或,,
综上可知:或或;
如图,设抛物线与的交点为,分别过作轴的垂线,垂足分别为,
∴,解得:,
∴,,
∵当时,始终位于直线的下方,
∴或,
解得:,
∴实数的取值范围为或.
答案第1页,共2页
答案第1页,共2页
2024年定海二中九年级上数学第一章二次函数质量监测
1.全卷共三大题,24小题,共8页。满分120分,考试时间120分钟。
2.全卷分卷I(选择题)和卷II(非选择题)两部分,全部在答题纸上作答。卷I的答案必须用2B铅笔填涂;卷II的答案必须用黑色钢笔或签字笔写在答题纸相应位置上。
3.考试时不能使用计算器。
第I卷(选择题)
选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.下列函数一定是二次函数的是( )
A. B.
C. D.
2.若是二次函数,则( )
A.7 B. C.或7 D.以上都不对
3.若二次函数的图象经过点,则该图象必经过点( )
A. B. C. D.
4.关于抛物线,下列说法中错误的是( )
A.开口方向向上 B.对称轴是直线
C.当时,y随x的增大而增大 D.顶点坐标为
5.在同一平面直角坐标系中,一次函数和二次函数的大致图象是( )
A. B.
C. D.
6.若抛物线与x轴有两个交点,则k的取值范围为( )
A. B. C.且 D.且
7.如图,正方形的边长为4cm,动点P、Q同时从点A出发,以的速度分别沿和的路径向点C运动,设运动时间为x(单位:s),四边形的面积为y(单位:cm2),则y与x()之间函数关系可以用图象表示为( )
A. B. C. D.
8.在平面直角坐标系中,直线与抛物线相交于,,且,则下列说法正确的是( )
A.若,m有最大值 B.若,m有最小值
C.若,m有最大值 D.若,m有最小值
9.已知二次函数,当时,随的增大而增大,则实数的取值范围是( )
A. B. C. D.
10.对于二次函数,规定函数是它的相关函数.已知点M,N的坐标分别为,,连接,若线段与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )
A.或 B.或
C.或 D.或
第II卷(非选择题)
二、填空题(本题有6小题,每题4分,共24分)
11.已知函数 是二次函数,那么 .
12.已知关于的二次函数,当时,的取值范围为
13.抛物线经过点,,以及点D,若点D的横坐标为,则点D的纵坐标是 (用n的式子含表示).
14.二次函数的最小值是 .
15.如图,抛物线与x轴交于点A、B(点A在B左侧),抛物线的顶点为C,点 D为抛物线上一点,且在对称轴右侧,若的面积为3,则点D的坐标为 .
16.如图(示意图),某跳水运动员进行10m跳台跳水训练,水面边缘点E的坐标为.运动员(将运动员看成一点)在空中运动的路线是经过原点O的抛物线.运动员在空中最高处点A的坐标为运动员入水后,运动路线为另一条抛物线,在该运动员入水点的正前方有M,N两点,且,该运动员入水后运动路线对应的抛物线的函数解析式为,且顶点C距水面5m,若该运动员出水点D在MN之间(包括M,N两点),则a的取值范围 .
解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.已知
(1)化简T.
(2)若a为二次函数的最小值,求此时的T值.
18.已知二次函数中,函数y与自变量x的部分对应值如下表:
0 2
5
(1)求二次函数的解析式;
(2)求该函数图象与x轴的交点坐标;
19.已知二次函数的顶点坐标是.
(1)当时,求该二次函数的表达式;
(2)在(1)的条件下,当时,求该二次函数的最大值
20.某游乐园有一个直径为米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心米处达到最高,高度为米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为 轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式.
(2)游乐园决定对喷水设施做如下设计改进,在喷出水柱的形状不变的前提下,把水池的直径扩大到 米,各方面喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合.请求出扩建改造后喷水池水柱的最大高度?
21.已知抛物线经过.
(1)求抛物线的表达式及对称轴;
(2)若是抛物线上不同的两点,且,求n的值;
(3)将抛物线沿x轴向左平移m()个单位长度,当时,它的函数值y的最小值为7,求m的值.
22.阅读与思考
下面是小明在数学笔记本上记录的父亲工厂里实际出现过的一个问题,请认真阅读,并帮助小明解答小明父亲给的以下任务:
小明父亲的工厂里加工一款纪念品,每件成本为元,投放景区内进行销售,售价不得低于成本价且利润率不高于,销售一段时间后市场调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:
销售单价x(元/件) … …
每天销售数量y(件) … …
(1)直接写出y与x的函数关系式;
(2)当销售单价为多少元时,每天获利最大?最大利润是多少元?
(3)若每天销售所得利润为元,那么销售单价应定为多少元?
任务一:要解决小明父亲提出的问题,主要运用的数学思想是________;
A.公理化思想 B.统计思想 C.函数思想 D.分类思想
任务二:请帮助小明解决相关的3个问题.
23.根据以下素材,探索完成任务
如何设计拱桥上救生圈的悬挂方案?
素材1 图1是一座抛物线形拱桥,以抛物线两个水平最低点连线为x轴,抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系,如图2所示. 某时测得水面宽,拱顶离水面最大距离为,抛物线拱形最高点与x轴的距离为.据调查,该河段水位在此基础上再涨达到最高.
素材2 为方便救助溺水者,拟在图1的桥拱上方栏杆处悬挂救生圈,如图3,救生圈悬挂点为了方便悬挂,救生圈悬挂点距离抛物线拱面上方,且相邻两救生圈悬挂点的水平间距为.为美观,放置后救生圈关于y轴成轴对称分布.(悬挂救生圈的柱子大小忽略不计)
任务1 确定桥拱形状 根据图2,求抛物线的函数表达式.
任务2 拟定设计方案 求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
任务3 探究救生绳长度 当水位达到最高时,上游个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
问题解决
(1)任务1:确定桥拱形状
根据图2,求抛物线的函数表达式.
(2)任务2:拟定设计方案
求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
(3)任务3:探究救生绳长度
当水位达到最高时,上游一个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
24.抛物线与轴交于、两点,与轴交于点,顶点为.
(1)求、两点的坐标;
(2)若为等边三角形,求的值;
(3)若,
①点是对称轴与的交点,点是抛物线上一点,且横坐标为,轴交于点,点,,构成的三角形是直角三角形,求的值;
②当时,始终位于直线的下方,求实数的取值范围.
第1页 共4页 第2页 共4页
第1页 共4页 第2页 共4页
参考答案:
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B B B C B D D B
二、填空题(本题有6小题,共24分)
11. 12. 13.
14. 15. 16.
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
17.(1)
,
∴.
(2),
∴二次函数的最小值为3,即,
∴.
18.解:(1)由题意,当
∴得.
将点,代入,
得,
解得,二次函数的解析式为;
(2)当时,,
解得:或,
该函数图象与轴的交点坐标,;
19.解:(1)根据题意可得,二次函数的顶点坐标是.
∴对称轴,
∵
∴,
∴二次函数的表达式为.
(2)如图,∵二次函数的表达式为,
∴当时,y的值随x值得增大而增大,
∵,
∴当时,y的值随x值得增大而增大,
∴当时,二次函数有最大值,
解得.
20.解(1)由喷出的水柱为抛物线,在距水池中心4米处达到最高,高度为6米,设水柱所在抛物线(第一象限部分)的函数表达式为,
将代入,得:,
解得:,
∴水柱所在抛物线(第一象限部分)的函数表达式为.
(2)当时, .
设改造后水柱所在抛物线(第一象限部分)的函数表达式为.
∵该函数图象过点,
∴,
解得:,
∴改造后水柱所在抛物线(第一象限部分)的函数表达式为,
∵
∴扩建改造后喷水池水柱的最大高度为米.
21.解(1)把点代入得,
,
解得:;
∴函数解析式为,
∴对称轴为
(2)由(1)得函数解析式为,
把代入得,,
∵
∴
∵是抛物线上不同的两点,
∴关于对称轴的对称,
∴.
∴.
(3)由(1)得函数解析式为,
∵此抛物线沿x轴向左平移m()个单位长度,
当向左平移时,平移后的解析式为,
∴对称轴为,
当时,顶点处取最小值,此时最小值为,不合题意;
当,时,当时y随x的增大而增大,
∴当时,有最小值7,即,
解得,(舍去),
综上所述,m的值为5.
22.解:任务一:由题意可得,
主要运用函数的数学思想,
故选:C;
任务二:(1)设,将,代入得,
,解得:,
∴,
∵售价不得低于成本价且利润率不高于,
∴,解得:,
∴;
(2)设利润为w,由题意可得,
∵,,
∴随增大而增大,
∴当时最大,
∴,
∴当销售单价为元时,每天获利最大,最大利润是元;
(3)当时,
,
解得:,(不符合题意舍去),
∴若每天销售所得利润为元,那么销售单价应定为元;
23.解(1)如图,知抛物线关于y轴对称,设解析式为,抛物线经过,,得,解得
∴.
(2)在,当,,解得或,
∴点
如题,相邻两救生圈悬挂点的水平间距为,且关于y轴成轴对称,
∵
∴左侧可挂3个,
由对称性只看右面,右面可挂3个,则此时最中间的两个救生圈的水平距离为,符合题意,
∴桥面一共可以挂6个救生圈,最右侧位于点上方处,即该点的坐标为.
(3)如图,当水位达到最高时,水位线为,
救生圈悬挂点距离抛物线拱面上方,当时,,,,
中,,
∴绳长至少需.
24.解(1)令,即,
∵,
∴,解得:,,
∴,;
(2)由,
∴,
由()得:,,
∴,,,
∵是等边三角形,
∴,
∴,解得:,
根据图象可知:,
∴;
(3)当时,,
令,则,
∴,
∴,
∴,
设直线解析式为,
∴,解得:,
∴解析式为,
∴当时,,
∴,
如图,当时,
∵,即轴,
∴,
∴,
∵的横坐标为,,
∴,,
∴,,
∴或,
整理得:或,
解得:(舍去)或,
如图,当时,
由上可知,,
由勾股定理得:,
∴,
∴或,
解得:(舍去)或,,
综上可知:或或;
如图,设抛物线与的交点为,分别过作轴的垂线,垂足分别为,
∴,解得:,
∴,,
∵当时,始终位于直线的下方,
∴或,
解得:,
∴实数的取值范围为或.
答案第1页,共2页
答案第1页,共2页
同课章节目录
