2.7探索勾股定理(1)课件(共18张PPT)2022-2023学年 数学浙教版八年级上册
文档属性
| 名称 | 2.7探索勾股定理(1)课件(共18张PPT)2022-2023学年 数学浙教版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 443.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 14:11:17 | ||
图片预览


文档简介
(共18张PPT)
2.7 探索勾股定理(1)
P
Q
R
a
c
b
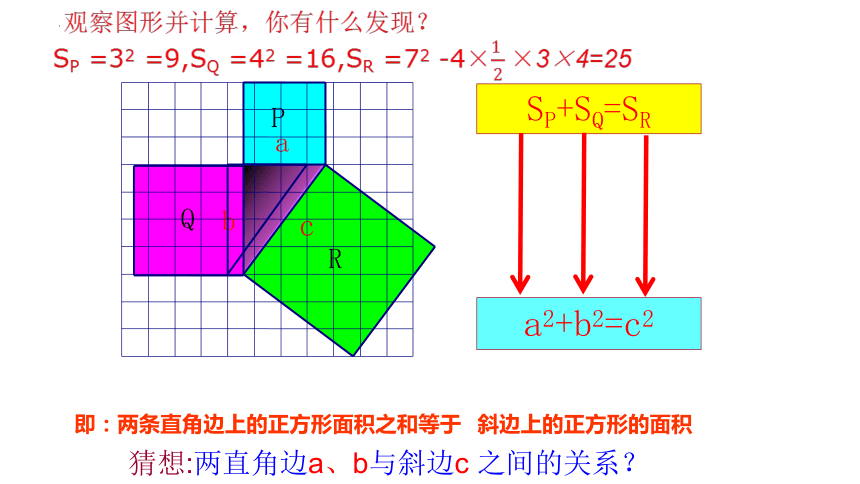
SP+SQ=SR
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
观察图形并计算,你有什么发现?
SP =32 =9,SQ =42 =16,SR =72 -4×3×4=25
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
a
c
b
a
b
c
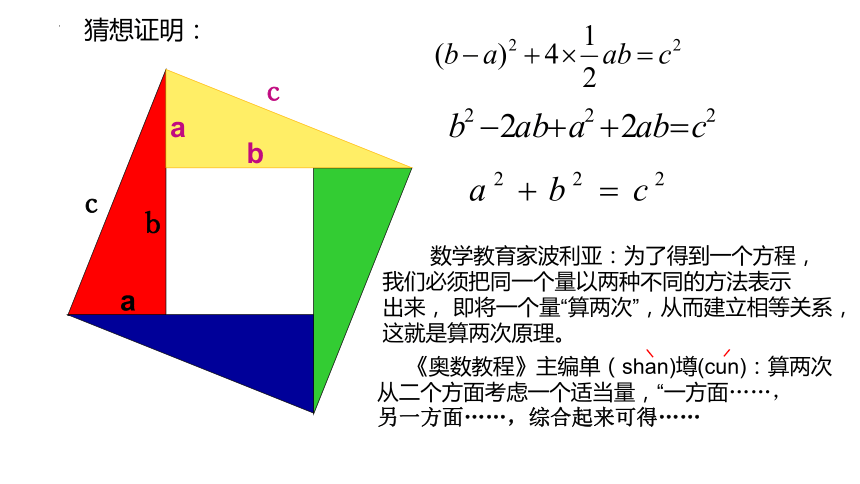
数学教育家波利亚:为了得到一个方程,
我们必须把同一个量以两种不同的方法表示
出来, 即将一个量“算两次”,从而建立相等关系,
这就是算两次原理。
《奥数教程》主编单(shan)壿(cun):算两次
从二个方面考虑一个适当量,“一方面……,
另一方面……,综合起来可得……
猜想证明:
a
b
c
a
b
c
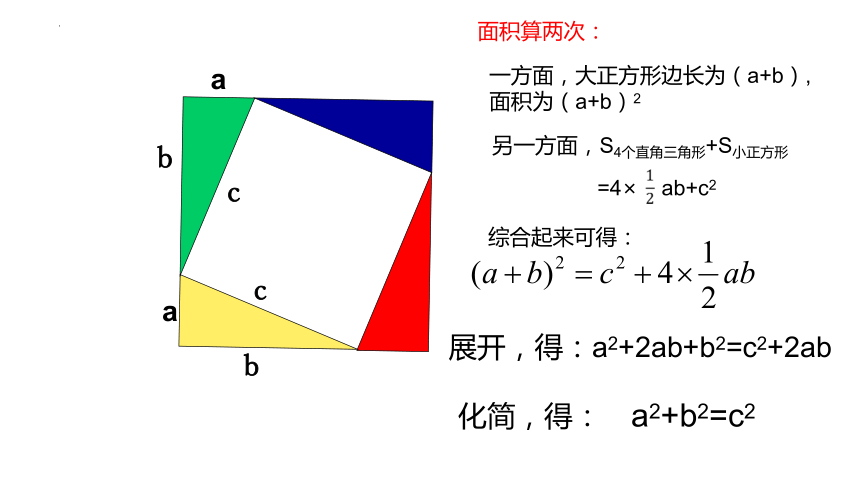
面积算两次:
一方面,大正方形边长为(a+b),
面积为(a+b)2
另一方面,S4个直角三角形+S小正方形
=4× ab+c2
综合起来可得:
展开,得:a2+2ab+b2=c2+2ab
化简,得:
a2+b2=c2
b
a
c
b
a
c
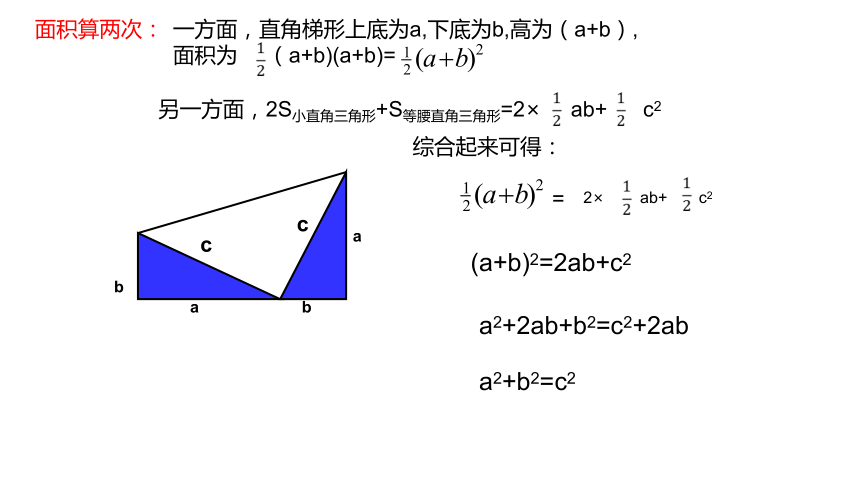
面积算两次:
综合起来可得:
(a+b)2=2ab+c2
一方面,直角梯形上底为a,下底为b,高为(a+b),
面积为 (a+b)(a+b)=
另一方面,2S小直角三角形+S等腰直角三角形=2× ab+ c2
=
2× ab+ c2
a2+2ab+b2=c2+2ab
a2+b2=c2
一般的,直角三角形的三条边长有下面的关系:
直角三角形两条直角边的平方和等于斜边的平方
如果a,b为直角三角形的两条直角边长,c为斜边长,则
a
b
c
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”因此这一性质也称为勾股定理.
勾
股
据《周髀算经》记载,西周开国时期(约公元前1000多年)有个叫商高的人对周公说,把一根直尺折成直角,两端连接得一直角三角形。如果钩是3,股是4,那么弦是5,这就是商高发现的“勾股定理”。因此在中国,勾股定理又称“商高定理”,在西方国家,勾股定理又称“毕达哥定理”。但毕达哥发现这一定理的时间要比商高迟得多,可见我国古代人民对人类贡献的杰出。
勾
股
赵爽
东汉至三国时代吴国人
为《周髀算经》作注,并著有《勾股圆方图说》
例1 已知在△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=c
(1)若 a=1, b=2, 求c;
(2)若 a=15, c=17, 求b.
c2=a2+b2=12 +22 =5
∵c>0,
解:(1)根据勾股定理,得
∴c=
(2)根据勾股定理,得
∵b>0 , ∴b=8.
=172 -152
=64.
=(17+15)(17-15)
b2 = c2 -a2
A
C
B
┚
a
b
c
例2 如图,是一个长方形零件图,根据所给的尺寸(单位:mm),求两孔中心A,B之间的距离.
A
B
C
40
90
160
40
解:过A作铅垂线,过B作水平线,两线交于点C,则∠C =90。
AC=90-40=50(mm),
BC=160-40=120(mm).
由勾股定理,得
AB2=AC2+BC2
=502+1202=16900(mm2)
∵AB>0
∴AB=130(mm).
答:两孔中心A,B之间的距离为130mm.
1.已知△ABC的三边分别是a,b,c,
若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
B
A
B
┚
C
当堂检测:
2.求下列直角三角形中未知边的长:
4
5
x
x= =3
.
x= =13
.
x= =
.
.
1
x
2
12
5
x
┑
3.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
x= =15
.
y= =5
.
z= =7
.
4.借助圆规和刻度尺, 在数轴上准确表示
-1
0
1
2
2
1
0
2
构造直角三角形,借助勾股定理解决
.
.
5. 在《九章算术》中记载了一道有趣的数学题:
“今有池方一丈,葭生其中央,
出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”
这道题的意思是说:有一个边长为一丈的正方形水池,在池的正中央长着一根芦苇,
芦苇露出水面一尺,若将芦苇拉到池边中点处,芦苇的顶端恰好与水面齐平,
问水有多深?芦苇有多长(1丈=10尺)?请你解决这个问题.
解;设水深为x尺,则芦苇长为(x+1)尺,1丈=10尺
根据勾股定理得:x2+52=(x+1)2 ,解得x=12
芦苇的长度=x+1=12+1=13(尺),
答:水池深12尺,芦苇长13尺.
连续递推,豁然开朗
7cm
6.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
A
B
C
D
50
40
30
7.有一根长为70cm的木棒,要放在长、宽、高分别是
50cm、40cm、30cm的木箱中,能放进去吗?
70cm
=
思维拓展,更上一层
=
A
B
C
D
>
70=
能
2.7 探索勾股定理(1)
P
Q
R
a
c
b
SP+SQ=SR
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
观察图形并计算,你有什么发现?
SP =32 =9,SQ =42 =16,SR =72 -4×3×4=25
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
a
c
b
a
b
c
数学教育家波利亚:为了得到一个方程,
我们必须把同一个量以两种不同的方法表示
出来, 即将一个量“算两次”,从而建立相等关系,
这就是算两次原理。
《奥数教程》主编单(shan)壿(cun):算两次
从二个方面考虑一个适当量,“一方面……,
另一方面……,综合起来可得……
猜想证明:
a
b
c
a
b
c
面积算两次:
一方面,大正方形边长为(a+b),
面积为(a+b)2
另一方面,S4个直角三角形+S小正方形
=4× ab+c2
综合起来可得:
展开,得:a2+2ab+b2=c2+2ab
化简,得:
a2+b2=c2
b
a
c
b
a
c
面积算两次:
综合起来可得:
(a+b)2=2ab+c2
一方面,直角梯形上底为a,下底为b,高为(a+b),
面积为 (a+b)(a+b)=
另一方面,2S小直角三角形+S等腰直角三角形=2× ab+ c2
=
2× ab+ c2
a2+2ab+b2=c2+2ab
a2+b2=c2
一般的,直角三角形的三条边长有下面的关系:
直角三角形两条直角边的平方和等于斜边的平方
如果a,b为直角三角形的两条直角边长,c为斜边长,则
a
b
c
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”因此这一性质也称为勾股定理.
勾
股
据《周髀算经》记载,西周开国时期(约公元前1000多年)有个叫商高的人对周公说,把一根直尺折成直角,两端连接得一直角三角形。如果钩是3,股是4,那么弦是5,这就是商高发现的“勾股定理”。因此在中国,勾股定理又称“商高定理”,在西方国家,勾股定理又称“毕达哥定理”。但毕达哥发现这一定理的时间要比商高迟得多,可见我国古代人民对人类贡献的杰出。
勾
股
赵爽
东汉至三国时代吴国人
为《周髀算经》作注,并著有《勾股圆方图说》
例1 已知在△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=c
(1)若 a=1, b=2, 求c;
(2)若 a=15, c=17, 求b.
c2=a2+b2=12 +22 =5
∵c>0,
解:(1)根据勾股定理,得
∴c=
(2)根据勾股定理,得
∵b>0 , ∴b=8.
=172 -152
=64.
=(17+15)(17-15)
b2 = c2 -a2
A
C
B
┚
a
b
c
例2 如图,是一个长方形零件图,根据所给的尺寸(单位:mm),求两孔中心A,B之间的距离.
A
B
C
40
90
160
40
解:过A作铅垂线,过B作水平线,两线交于点C,则∠C =90。
AC=90-40=50(mm),
BC=160-40=120(mm).
由勾股定理,得
AB2=AC2+BC2
=502+1202=16900(mm2)
∵AB>0
∴AB=130(mm).
答:两孔中心A,B之间的距离为130mm.
1.已知△ABC的三边分别是a,b,c,
若∠B=Rt∠,则有关系式( )
A.a2+b2=c2
B.a2+c2=b2
C.a2-b2=c2
D.b2+c2=a2
B
A
B
┚
C
当堂检测:
2.求下列直角三角形中未知边的长:
4
5
x
x= =3
.
x= =13
.
x= =
.
.
1
x
2
12
5
x
┑
3.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
x= =15
.
y= =5
.
z= =7
.
4.借助圆规和刻度尺, 在数轴上准确表示
-1
0
1
2
2
1
0
2
构造直角三角形,借助勾股定理解决
.
.
5. 在《九章算术》中记载了一道有趣的数学题:
“今有池方一丈,葭生其中央,
出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”
这道题的意思是说:有一个边长为一丈的正方形水池,在池的正中央长着一根芦苇,
芦苇露出水面一尺,若将芦苇拉到池边中点处,芦苇的顶端恰好与水面齐平,
问水有多深?芦苇有多长(1丈=10尺)?请你解决这个问题.
解;设水深为x尺,则芦苇长为(x+1)尺,1丈=10尺
根据勾股定理得:x2+52=(x+1)2 ,解得x=12
芦苇的长度=x+1=12+1=13(尺),
答:水池深12尺,芦苇长13尺.
连续递推,豁然开朗
7cm
6.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
A
B
C
D
50
40
30
7.有一根长为70cm的木棒,要放在长、宽、高分别是
50cm、40cm、30cm的木箱中,能放进去吗?
70cm
=
思维拓展,更上一层
=
A
B
C
D
>
70=
能
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
