2.7探索勾股定理(2)课件(共12张PPT) 2022--2023学年浙教版八年级数学上册
文档属性
| 名称 | 2.7探索勾股定理(2)课件(共12张PPT) 2022--2023学年浙教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 390.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-23 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
2.7探索勾股定理(2)
旧知回顾,引入新知
a
b
c
直角三角形两条直角边的平方和等于斜边的平方
(勾股定理)
a2+b2=c2
逆命题:如果一个三角形两条边的平方和等于第三条边的平方。
请问:这个三角形是直角三角形吗?
实验操作,探究新知
请同学们动手借助圆规、直尺画一个边长为3,4,5的三角形,然后用量角器测 量最大角的度数,验证边长为3, 4,5的三角形是否是直角三角形
根据上述结果,联系视频材料,你能得到什么猜想呢?
实验操作,探究新知
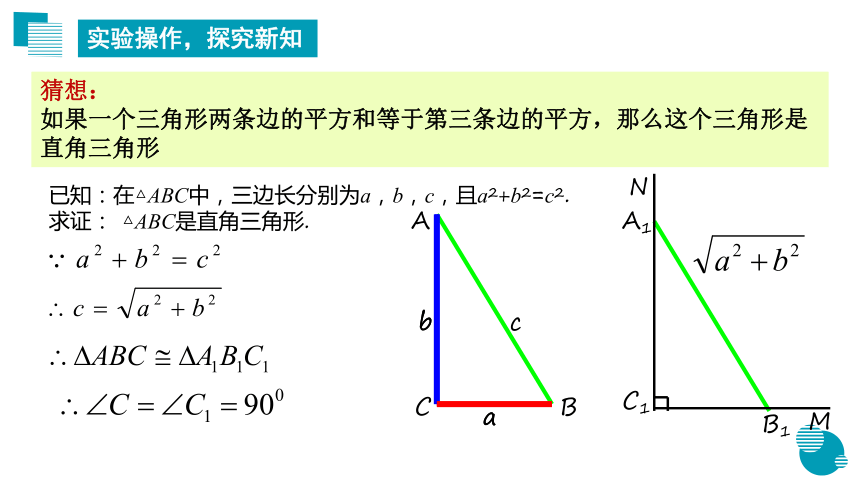
猜想:
如果一个三角形两条边的平方和等于第三条边的平方,那么这个三角形是直角三角形
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
求证: △ABC是直角三角形.
a
c
b
A
C
B
b
a
N
B1
A1
C1
M
实验操作,探究新知
数
形
∵
△ABC
是直角三角形
a
b
c
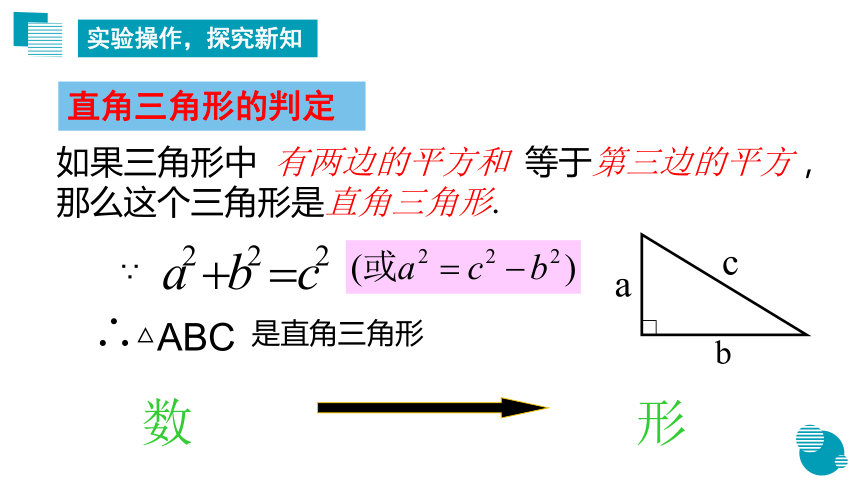
如果三角形中 有两边的平方和 等于第三边的平方,那么这个三角形是直角三角形.
直角三角形的判定
辨析:下列三边组成的三角形是直角三角形吗
解:(2) ∵
∴此三角形是直角三角形.
一定 最长边
二算“平方式”
小试牛刀,应用新知
例1:根据下列条件,分别判别a,b,c为边的三角形是不是直角三角形.
(3) a : b : c = 5 : 12 : 13
(1) a=24,b=25,c=7
(2)
解:(3) 设a=5k,b=12k,c=13k (k>0)
∵(5k)2+(12k)2=(13k)2
∴此三角形是直角三角形
小试牛刀,应用新知
例2:已知△ABC三条边长分别为a,b,c,且a=m +n ,b=2mn,c=m -n (m>n,且均为正整数),△ABC是直角三角形吗?请说明理由.
证明:
∵a>c,a-b=(m-n) >0
∴a为最大边
∵b +c =m4+2m n +n4=(m +n ) =a
∴△ABC是直角三角形
小试牛刀,应用新知
例3:如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,求四边形ABCD的面积S.
解:连结AC
在Rt△ABC中
∵ AB=3,BC=4
∴
∵CD=12,AD=13
∴
∴ △ACD为直角三角形
且 ∠ACD=Rt∠
∴
小试牛刀,应用新知
拓展提升,巩固新知
已知这三个正方形构成的图形中,绿色部分的面积与蓝色部分的面积相等,则△ABC是直角三角形吗 请证明你的判断
如图,在一个4×4的网格中有一个△ABC,A、B、C均在格点上,请判定它是否是直角三角形?你有多少种判定的方法?
课后挑战
设计意图:本题是对小结内容的应用,让学生充分掌握直角三角形判定的几种方法,并能根据题目条件选择最合适的方法,在网格三角形中,往往利用边长,也就是勾股定理逆定理来判断。
如图,在一个4×4的网格中有一个△ABC,A、B、C均在格点上,请判定它是否是直角三角形?你有多少种判定的方法?
归纳小结,作业布置
2.7探索勾股定理(2)
旧知回顾,引入新知
a
b
c
直角三角形两条直角边的平方和等于斜边的平方
(勾股定理)
a2+b2=c2
逆命题:如果一个三角形两条边的平方和等于第三条边的平方。
请问:这个三角形是直角三角形吗?
实验操作,探究新知
请同学们动手借助圆规、直尺画一个边长为3,4,5的三角形,然后用量角器测 量最大角的度数,验证边长为3, 4,5的三角形是否是直角三角形
根据上述结果,联系视频材料,你能得到什么猜想呢?
实验操作,探究新知
猜想:
如果一个三角形两条边的平方和等于第三条边的平方,那么这个三角形是直角三角形
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
求证: △ABC是直角三角形.
a
c
b
A
C
B
b
a
N
B1
A1
C1
M
实验操作,探究新知
数
形
∵
△ABC
是直角三角形
a
b
c
如果三角形中 有两边的平方和 等于第三边的平方,那么这个三角形是直角三角形.
直角三角形的判定
辨析:下列三边组成的三角形是直角三角形吗
解:(2) ∵
∴此三角形是直角三角形.
一定 最长边
二算“平方式”
小试牛刀,应用新知
例1:根据下列条件,分别判别a,b,c为边的三角形是不是直角三角形.
(3) a : b : c = 5 : 12 : 13
(1) a=24,b=25,c=7
(2)
解:(3) 设a=5k,b=12k,c=13k (k>0)
∵(5k)2+(12k)2=(13k)2
∴此三角形是直角三角形
小试牛刀,应用新知
例2:已知△ABC三条边长分别为a,b,c,且a=m +n ,b=2mn,c=m -n (m>n,且均为正整数),△ABC是直角三角形吗?请说明理由.
证明:
∵a>c,a-b=(m-n) >0
∴a为最大边
∵b +c =m4+2m n +n4=(m +n ) =a
∴△ABC是直角三角形
小试牛刀,应用新知
例3:如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,求四边形ABCD的面积S.
解:连结AC
在Rt△ABC中
∵ AB=3,BC=4
∴
∵CD=12,AD=13
∴
∴ △ACD为直角三角形
且 ∠ACD=Rt∠
∴
小试牛刀,应用新知
拓展提升,巩固新知
已知这三个正方形构成的图形中,绿色部分的面积与蓝色部分的面积相等,则△ABC是直角三角形吗 请证明你的判断
如图,在一个4×4的网格中有一个△ABC,A、B、C均在格点上,请判定它是否是直角三角形?你有多少种判定的方法?
课后挑战
设计意图:本题是对小结内容的应用,让学生充分掌握直角三角形判定的几种方法,并能根据题目条件选择最合适的方法,在网格三角形中,往往利用边长,也就是勾股定理逆定理来判断。
如图,在一个4×4的网格中有一个△ABC,A、B、C均在格点上,请判定它是否是直角三角形?你有多少种判定的方法?
归纳小结,作业布置
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
