1.2不同条件下种群的增长方式不同(教学课件)(共26张PPT)-高中生物学浙科版(2019)选择性必修二
文档属性
| 名称 | 1.2不同条件下种群的增长方式不同(教学课件)(共26张PPT)-高中生物学浙科版(2019)选择性必修二 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙科版(2019) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2024-09-26 12:33:42 | ||
图片预览






文档简介
(共26张PPT)
第二节 不同条件下种群的增长方式不同
研究种群的核心问题是种群数量的变化规律
一 、活动 探究果蝇种群的增长
1.目的要求 (1)学会培养果蝇的方法与技能。
(2)分析果蝇的数量变化,绘制果蝇增长的曲线图,学会数学建模的方法。
2.探究问题 (1)不同环境条件下果蝇种群是以什么方式增长的
(2)果蝇种群的这种增长方式有何规律
3、材料 要求计数21天,获得这4只果蝇一个世代全部子代的数量变化。
4、方法步骤
(1)取3个500 mL广口瓶,先在每个广口瓶底部铺一层厚约2 cm的棉花,然后放入大小相等且熟透了的半根香蕉、
2只雌果蝇和2只雄果蝇,最后用双层纱布盖住瓶口,并用橡皮筋扎紧,作为果蝇培养瓶。
(2)将培养瓶置于温度适宜(20~25 ℃)的环境中培养。
防止实验偶然性。
吸收香蕉腐败的汁液;为果蝇化蛹提供场所,所以棉花层不宜过薄不然香蕉汁液会没过棉花,会影响蛹后果蝇的羽化。
作为食物。
(3)每天观察、记录培养瓶中果蝇个体数,持续3周。若培养瓶内的果蝇数量不易直接观察计数时,另取一洁净广口瓶作为果蝇的麻醉瓶,放入滴有1~2滴乙醚的棉花团,并将其与培养瓶的瓶口对接,轻拍培养瓶把果蝇赶入麻醉瓶。待果蝇麻醉后,将其全部倒在白纸上,用毛笔进行计数。计数结束后再将这些果蝇放回培养瓶中培养。
将果蝇麻醉,便于计数。
注意:乙醚不能过多,以免麻醉过度。若果蝇翅膀与身体呈45角翘起说明已经死亡。
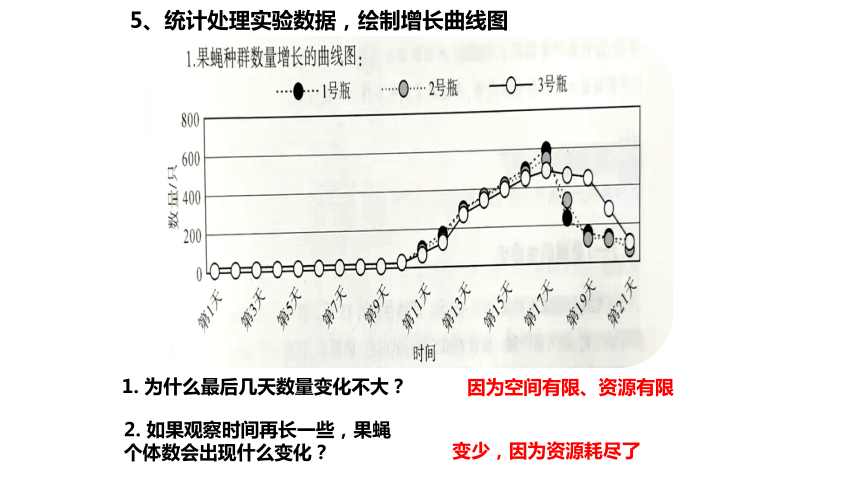
5、统计处理实验数据,绘制增长曲线图
1. 为什么最后几天数量变化不大?
因为空间有限、资源有限
2. 如果观察时间再长一些,果蝇个体数会出现什么变化?
变少,因为资源耗尽了
二、建立数学模型是解释种群数量变化的重要方法
1.数学模型:用来描述现实系统或其性质的一个抽象简化的数学结构。
2.数学模型的表现形式:数学方程式或曲线图。
3.建构数学模型的意义:描述、解释和预测种群数量的变化。
4.高中阶段的模型有数学模型、物理模型、概念模型。
探究——科学探究
下面是某种细菌在某条件下分裂繁殖的规律。
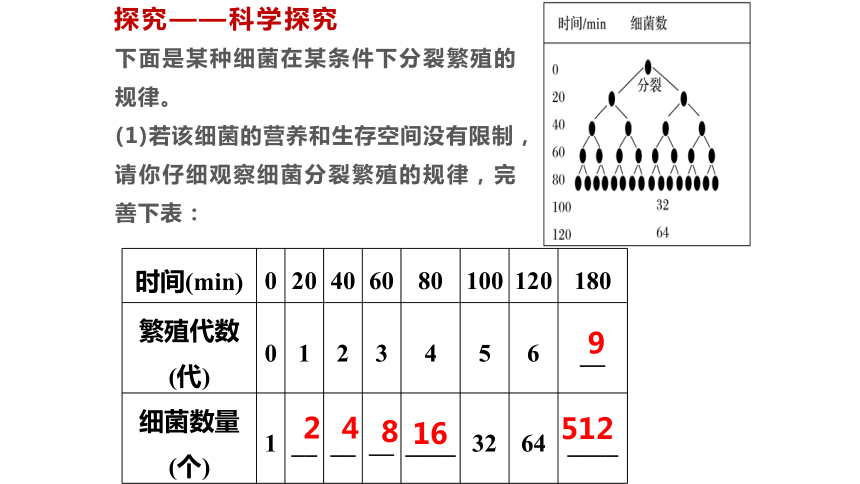
(1)若该细菌的营养和生存空间没有限制,请你仔细观察细菌分裂繁殖的规律,完善下表:
时间(min) 0 20 40 60 80 100 120 180
繁殖代数(代) 0 1 2 3 4 5 6 __
细菌数量(个) 1 __ __ __ ____ 32 64 ____
2
4
8
16
512
9
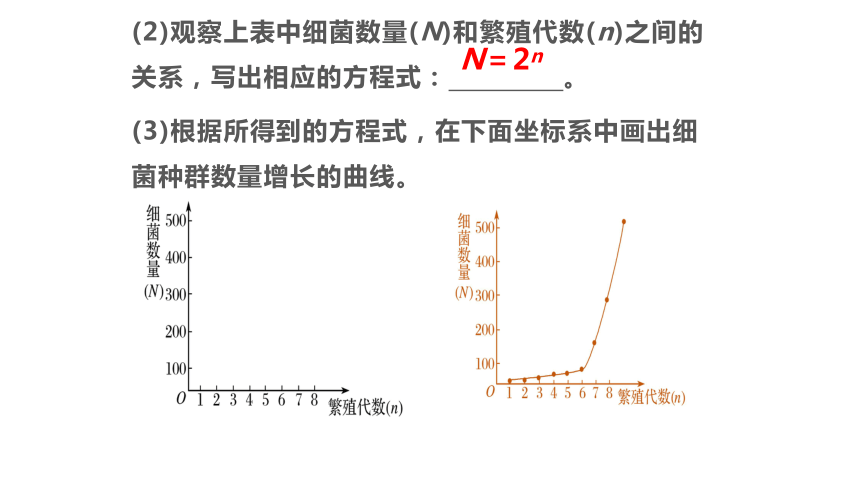
(2)观察上表中细菌数量(N)和繁殖代数(n)之间的关系,写出相应的方程式: 。
(3)根据所得到的方程式,在下面坐标系中画出细菌种群数量增长的曲线。
N=2n
(4)我们从曲线的走向分析可以预计:
①在资源无限、空间无限和不受其他生物制约的理想条件下,细菌种群的增长不会受 的影响,即在理想条件下种群增长的曲线为“ ”形。
②类比前述细菌种群数量模型构建过程,若在食物和空间条件充裕、气候适宜、没有敌害等条件下,某种群的起始数量为N0,并且第二年的数量是第一年的λ倍(该种群每年的增长倍数都保持不变),则:
a.一年后种群数量N1= ,两年后种群数量N2= ,t年后种群数量Nt= (t为时间,Nt表示t年后该种群的数量)。
种群密度增加
J
N0×λ
N0×λ2
N0×λt
在调查某林场松鼠的种群数量时,计算当年种群数量与前一年种群数量的比值(λ),并得到如右图所示的曲线,则该种群在第几年时种群数量最少呢
① λ>1,种群数量增长
② λ=1,种群数量不变
③ 0<λ<1,种群数量下降
分析当λ>1、λ=1、0<λ<1时,种群的数量变化和年龄结构的类型。
b.若λ>1,请在坐标系中绘出数学方程式Nt=N0λt 中种群数量Nt
随t 的变化曲线图。
(5)总结:
①“J”形增长曲线形成的条件:
资源无限、空间无限、不受其他生物制约;
②适用范围: a.实验室条件下;
b.生态入侵;
c.引种到一个适宜的新环境中的早期。
三、种群在无限环境条件下呈指数增长
指数增长曲线:
又称“J”形增长
资源
空间
理想条件
很慢
快
公式为:Nt=Noλt
思考:1.种群在指数增长过程中,增长率和增长速率是否改变?
增长率=(现有个体数-原有个体数)/原有个体数
增长速率=(现有个体数-原有个体数)/增长时间
不变,即λ-1
逐渐增大
种群的增长率和增长速率
种群在单位时间内新增加的个体数与原有数量的比例。
计算公式:
增长率=(本次总数-上次总数)/上次总数 =出生率-死亡率
增长率:
增长速率:
种群在单位时间内新增加的个体数。
计算公式:
增长速率=(本次总数-上次总数)/单位时间 =曲线的斜率
种群爆炸
生物种群繁殖不可能不受环境制约。当生殖率大于死亡率,种群超常繁殖时,种群数量激增,生态学家将这种现象称为种群“爆炸”。
害虫防治专家则把这种现象称为害虫猖獗或害虫大发生。
实例:高斯对大草履虫种群研究的实验
高斯把5个大草履虫置于0.5 mL的培养液中,每隔24小时统计一次草履虫的数量,经过反复实验,结果如下:
时间(天) 1 2 3 4 5 6
种群中个体数量 20 137 319 369 375 365
每天的增长速率 —— 117 182 50 6 -10
每天的增长率 —— 5.85 1.33 0.16 0.02 -0.03
逻辑斯谛增长——S型增长曲线
Q1.大草履虫的种群为什么不呈指数增长?
Q2.其种群数量增长过程是怎样的?
Q3.其种群数量达到基本稳定的数量值称做什么?
实例:高斯对大草履虫种群研究的实验
高斯把5个大草履虫置于0.5 mL的培养液中,每隔24小时统计一次草履虫的数量,经过反复实验,结果如下:
时间(天) 1 2 3 4 5 6
种群中个体数量 20 137 319 369 375 365
每天的增长速率 —— 117 182 50 6 -10
每天的增长率 —— 5.85 1.33 0.16 0.02 -0.03
逻辑斯谛增长——S形增长曲线
K值:即环境容纳量。指长时期内,环境条件所能维持的种群最大数量。
Q.同一种群的K值固定不变吗?
K值大小由环境中的有效资源决定,会根据环境条件的改变而变化。
Q.种群数量达到K值时,都能在K值维持恒定吗?
·
K/2
k值只代表种群数量的一个平均值,在环境不遭受破坏的条件下,实际的种群数量在这个平均值的上下波动。所以K值是种群在该环境中的稳定平衡密度。
K值
原因:存在环境阻力——自然界中食物和空间等资源总是有限的,当种群密度增大时,种内斗争和种间竞争会不断加剧,捕食者数量也会不断增加,还有气候、传染病等因素作用,导致该种群的出生率降低,死亡率增高(即种群增长率不断下降),当出生率与死亡率相等(即增长率为0)时,种群的增长就会停止,有时会稳定在一定的水平。
Q.种群数量达到K值时,都能在K值维持恒定吗?
·
K/2
K值
种群数量小于K/2时,种群增长逐渐加快;
种群数量等于K/2时,种群增长最快;
种群数量大于K/2时, 种群增长逐渐减慢;
种群数量达到K值时,种群增长停止或在K值上下波动
K/2时种群的增长速率最快,
K值时种群数量最大,但增长速率为0
小结:种群的逻辑斯谛增长
①产生条件:
存在环境阻力
有限条件——资源有限,空间有限,受其他生物制约
③增长特点:
起始呈加速增长,K/2时增长最快,此后开始减速增长,到达K值时停止增长或在K值上下波动。
②数学模型:
S 形曲线
增长速率是先上升,后下降,
而增长率逐渐下降。
开始期
加快
转折期
减速期
思考:1.在“S”形增长曲线中,有一段时期近似于“J”形增长曲线,这一段是否等同于“J”形增长曲线
“S”形曲线
“J”形曲线
阴影部分为环境阻力导致,实际为生存斗争中被淘汰的个体
环境阻力:指妨碍生物潜能实现的环境因子的总和,包括生物因子和非生物因子
(2)对于濒危野生动物的保护,可通过改善生存环境来增大环境容纳量;
(3)对于有害生物的防治,应通过限制环境因素来降低环境容纳量。
应用
(1)
讨论:家鼠繁殖力极强,善于打洞,偷吃粮食,传播疾病危害极大,请同学们讨论应该采取哪些措施控制家鼠数量?
老鼠
机械捕杀
药物捕杀
施用性诱捕剂
养殖或释放天敌(猫)
将食物储存在安全处
降低
出生率率
减少数量
增大环境阻力
降低环境容纳量
打扫卫生
硬化地面
增长方式 指数增长 逻辑斯谛增长
增长曲线 J型曲线 S型曲线
形成条件 资源无限、空间无限、不受其他生物制约 资源有限、空间有限、受其他生物制约
适用范围 理想条件 自然条件
K值 无 有
增长率变化 保持稳定不变 逐渐下降
增长速率变化 一直增大 先上升,到K/2后下降
指数增长和逻辑斯谛增长的区别
第二节 不同条件下种群的增长方式不同
研究种群的核心问题是种群数量的变化规律
一 、活动 探究果蝇种群的增长
1.目的要求 (1)学会培养果蝇的方法与技能。
(2)分析果蝇的数量变化,绘制果蝇增长的曲线图,学会数学建模的方法。
2.探究问题 (1)不同环境条件下果蝇种群是以什么方式增长的
(2)果蝇种群的这种增长方式有何规律
3、材料 要求计数21天,获得这4只果蝇一个世代全部子代的数量变化。
4、方法步骤
(1)取3个500 mL广口瓶,先在每个广口瓶底部铺一层厚约2 cm的棉花,然后放入大小相等且熟透了的半根香蕉、
2只雌果蝇和2只雄果蝇,最后用双层纱布盖住瓶口,并用橡皮筋扎紧,作为果蝇培养瓶。
(2)将培养瓶置于温度适宜(20~25 ℃)的环境中培养。
防止实验偶然性。
吸收香蕉腐败的汁液;为果蝇化蛹提供场所,所以棉花层不宜过薄不然香蕉汁液会没过棉花,会影响蛹后果蝇的羽化。
作为食物。
(3)每天观察、记录培养瓶中果蝇个体数,持续3周。若培养瓶内的果蝇数量不易直接观察计数时,另取一洁净广口瓶作为果蝇的麻醉瓶,放入滴有1~2滴乙醚的棉花团,并将其与培养瓶的瓶口对接,轻拍培养瓶把果蝇赶入麻醉瓶。待果蝇麻醉后,将其全部倒在白纸上,用毛笔进行计数。计数结束后再将这些果蝇放回培养瓶中培养。
将果蝇麻醉,便于计数。
注意:乙醚不能过多,以免麻醉过度。若果蝇翅膀与身体呈45角翘起说明已经死亡。
5、统计处理实验数据,绘制增长曲线图
1. 为什么最后几天数量变化不大?
因为空间有限、资源有限
2. 如果观察时间再长一些,果蝇个体数会出现什么变化?
变少,因为资源耗尽了
二、建立数学模型是解释种群数量变化的重要方法
1.数学模型:用来描述现实系统或其性质的一个抽象简化的数学结构。
2.数学模型的表现形式:数学方程式或曲线图。
3.建构数学模型的意义:描述、解释和预测种群数量的变化。
4.高中阶段的模型有数学模型、物理模型、概念模型。
探究——科学探究
下面是某种细菌在某条件下分裂繁殖的规律。
(1)若该细菌的营养和生存空间没有限制,请你仔细观察细菌分裂繁殖的规律,完善下表:
时间(min) 0 20 40 60 80 100 120 180
繁殖代数(代) 0 1 2 3 4 5 6 __
细菌数量(个) 1 __ __ __ ____ 32 64 ____
2
4
8
16
512
9
(2)观察上表中细菌数量(N)和繁殖代数(n)之间的关系,写出相应的方程式: 。
(3)根据所得到的方程式,在下面坐标系中画出细菌种群数量增长的曲线。
N=2n
(4)我们从曲线的走向分析可以预计:
①在资源无限、空间无限和不受其他生物制约的理想条件下,细菌种群的增长不会受 的影响,即在理想条件下种群增长的曲线为“ ”形。
②类比前述细菌种群数量模型构建过程,若在食物和空间条件充裕、气候适宜、没有敌害等条件下,某种群的起始数量为N0,并且第二年的数量是第一年的λ倍(该种群每年的增长倍数都保持不变),则:
a.一年后种群数量N1= ,两年后种群数量N2= ,t年后种群数量Nt= (t为时间,Nt表示t年后该种群的数量)。
种群密度增加
J
N0×λ
N0×λ2
N0×λt
在调查某林场松鼠的种群数量时,计算当年种群数量与前一年种群数量的比值(λ),并得到如右图所示的曲线,则该种群在第几年时种群数量最少呢
① λ>1,种群数量增长
② λ=1,种群数量不变
③ 0<λ<1,种群数量下降
分析当λ>1、λ=1、0<λ<1时,种群的数量变化和年龄结构的类型。
b.若λ>1,请在坐标系中绘出数学方程式Nt=N0λt 中种群数量Nt
随t 的变化曲线图。
(5)总结:
①“J”形增长曲线形成的条件:
资源无限、空间无限、不受其他生物制约;
②适用范围: a.实验室条件下;
b.生态入侵;
c.引种到一个适宜的新环境中的早期。
三、种群在无限环境条件下呈指数增长
指数增长曲线:
又称“J”形增长
资源
空间
理想条件
很慢
快
公式为:Nt=Noλt
思考:1.种群在指数增长过程中,增长率和增长速率是否改变?
增长率=(现有个体数-原有个体数)/原有个体数
增长速率=(现有个体数-原有个体数)/增长时间
不变,即λ-1
逐渐增大
种群的增长率和增长速率
种群在单位时间内新增加的个体数与原有数量的比例。
计算公式:
增长率=(本次总数-上次总数)/上次总数 =出生率-死亡率
增长率:
增长速率:
种群在单位时间内新增加的个体数。
计算公式:
增长速率=(本次总数-上次总数)/单位时间 =曲线的斜率
种群爆炸
生物种群繁殖不可能不受环境制约。当生殖率大于死亡率,种群超常繁殖时,种群数量激增,生态学家将这种现象称为种群“爆炸”。
害虫防治专家则把这种现象称为害虫猖獗或害虫大发生。
实例:高斯对大草履虫种群研究的实验
高斯把5个大草履虫置于0.5 mL的培养液中,每隔24小时统计一次草履虫的数量,经过反复实验,结果如下:
时间(天) 1 2 3 4 5 6
种群中个体数量 20 137 319 369 375 365
每天的增长速率 —— 117 182 50 6 -10
每天的增长率 —— 5.85 1.33 0.16 0.02 -0.03
逻辑斯谛增长——S型增长曲线
Q1.大草履虫的种群为什么不呈指数增长?
Q2.其种群数量增长过程是怎样的?
Q3.其种群数量达到基本稳定的数量值称做什么?
实例:高斯对大草履虫种群研究的实验
高斯把5个大草履虫置于0.5 mL的培养液中,每隔24小时统计一次草履虫的数量,经过反复实验,结果如下:
时间(天) 1 2 3 4 5 6
种群中个体数量 20 137 319 369 375 365
每天的增长速率 —— 117 182 50 6 -10
每天的增长率 —— 5.85 1.33 0.16 0.02 -0.03
逻辑斯谛增长——S形增长曲线
K值:即环境容纳量。指长时期内,环境条件所能维持的种群最大数量。
Q.同一种群的K值固定不变吗?
K值大小由环境中的有效资源决定,会根据环境条件的改变而变化。
Q.种群数量达到K值时,都能在K值维持恒定吗?
·
K/2
k值只代表种群数量的一个平均值,在环境不遭受破坏的条件下,实际的种群数量在这个平均值的上下波动。所以K值是种群在该环境中的稳定平衡密度。
K值
原因:存在环境阻力——自然界中食物和空间等资源总是有限的,当种群密度增大时,种内斗争和种间竞争会不断加剧,捕食者数量也会不断增加,还有气候、传染病等因素作用,导致该种群的出生率降低,死亡率增高(即种群增长率不断下降),当出生率与死亡率相等(即增长率为0)时,种群的增长就会停止,有时会稳定在一定的水平。
Q.种群数量达到K值时,都能在K值维持恒定吗?
·
K/2
K值
种群数量小于K/2时,种群增长逐渐加快;
种群数量等于K/2时,种群增长最快;
种群数量大于K/2时, 种群增长逐渐减慢;
种群数量达到K值时,种群增长停止或在K值上下波动
K/2时种群的增长速率最快,
K值时种群数量最大,但增长速率为0
小结:种群的逻辑斯谛增长
①产生条件:
存在环境阻力
有限条件——资源有限,空间有限,受其他生物制约
③增长特点:
起始呈加速增长,K/2时增长最快,此后开始减速增长,到达K值时停止增长或在K值上下波动。
②数学模型:
S 形曲线
增长速率是先上升,后下降,
而增长率逐渐下降。
开始期
加快
转折期
减速期
思考:1.在“S”形增长曲线中,有一段时期近似于“J”形增长曲线,这一段是否等同于“J”形增长曲线
“S”形曲线
“J”形曲线
阴影部分为环境阻力导致,实际为生存斗争中被淘汰的个体
环境阻力:指妨碍生物潜能实现的环境因子的总和,包括生物因子和非生物因子
(2)对于濒危野生动物的保护,可通过改善生存环境来增大环境容纳量;
(3)对于有害生物的防治,应通过限制环境因素来降低环境容纳量。
应用
(1)
讨论:家鼠繁殖力极强,善于打洞,偷吃粮食,传播疾病危害极大,请同学们讨论应该采取哪些措施控制家鼠数量?
老鼠
机械捕杀
药物捕杀
施用性诱捕剂
养殖或释放天敌(猫)
将食物储存在安全处
降低
出生率率
减少数量
增大环境阻力
降低环境容纳量
打扫卫生
硬化地面
增长方式 指数增长 逻辑斯谛增长
增长曲线 J型曲线 S型曲线
形成条件 资源无限、空间无限、不受其他生物制约 资源有限、空间有限、受其他生物制约
适用范围 理想条件 自然条件
K值 无 有
增长率变化 保持稳定不变 逐渐下降
增长速率变化 一直增大 先上升,到K/2后下降
指数增长和逻辑斯谛增长的区别
同课章节目录
