浙教(2024)七年级上册-4.1列代数式 课件(15张PPT)
文档属性
| 名称 | 浙教(2024)七年级上册-4.1列代数式 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-03 22:33:18 | ||
图片预览






文档简介
(共15张PPT)
一条隧道长L米,一列火车长 180米。如果该列火车穿过隧道所花的时间为t分,则列车的速度怎么表示
情景引入
答:列车的为
情景引入
4.1 列代数式
第三章 代数式
1、通过实例经历代数式概念产生的过程。
2、了解代数式的概念。
3、能分析具体问题中的简单数量关系,并用代数式表示。
学习目标
(1)大米的单价为每千克a元,食用油的单价为每千克b元。买10千克大米、2千克食用油共需_________元。
知识点讲解
请回答下面的问题:
(2)日平均气温是指一天中2:00,8:00,14:00,20:00 四个时刻气温的平均值。若某天上述四个时刻气温的摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数是__________。
(10a+b)
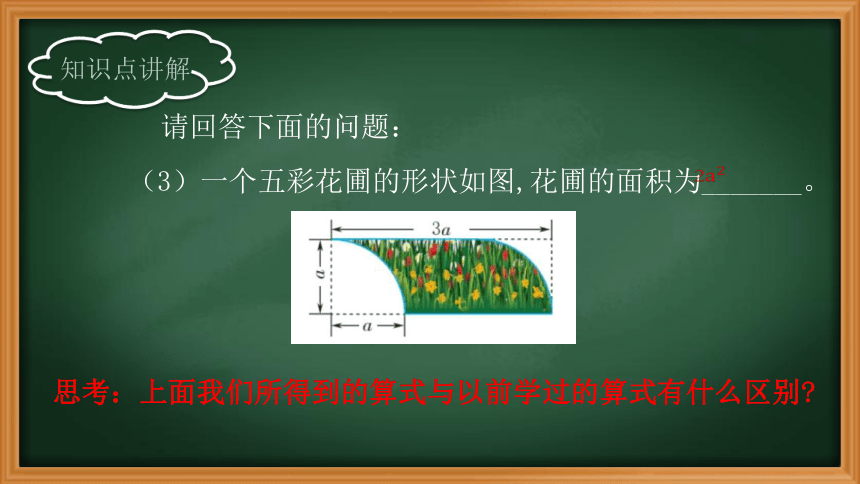
(3)一个五彩花圃的形状如图,花圃的面积为_______。
知识点讲解
请回答下面的问题:
2
思考:上面我们所得到的算式与以前学过的算式有什么区别
知识点讲解
像10a+26, ,2, 这样, 由数、表示数的字母和运算符号组成的数学表达式称为代数式。
这里的运算是指加、減、乘、除、乘方和开方。单独一个数或者一个字母也称代数式。
例1 用代数式表示:
(1)x的3倍与3的差:_________。
(2)x的2倍与y的的和:_________。
(3)a与b的和的平方:________。
(4)2a的立方根:__________。
例题练一练
3x-3
2x+y
知识点讲解
代数式可以简明地、具有普遍意义地表示实际问题中的量,给数量关系的研究带来方便。
例2 一辆汽车以80km/h的速度行驶,从A城到B城需t(h)。如果该车的行驶速度增加v (km/h),那么从A城到B城需多少时间
例题练一练
A城
B城
解:由题意得,A,B两城之间的路程为80t(km)。如果该车的行驶速度增加v(km/h),那么汽车的行驶速度为(80+v)km/h,此时从A城到B城需 (h)。
答:若该车的行驶速度增加v(km/h),则从A城到B城需 (h)。
例题练一练
课内练习
1、用代数式表示:
(1)a与b的的和:_________
(2)a与b的平方的差:_________
(3)m与n的差的平方:_________
(4),和除以s所得的商:_________
(5) x与1的差的平方根:_________
a+
a-
±
课内练习
2、已知甲数比乙数的2倍少1。设乙数为x,用关于x的代数式表示甲数。
解:甲数的表达式是2x-1。
课内练习
3、举一个用代数式 3a+2b表示结果的实际问题的例子。
举例:苹果每千克a元,桃子每千克b元,购买3千克苹果、2千克桃子共需(3a+2b)元。
感悟与反思
一条隧道长L米,一列火车长 180米。如果该列火车穿过隧道所花的时间为t分,则列车的速度怎么表示
情景引入
答:列车的为
情景引入
4.1 列代数式
第三章 代数式
1、通过实例经历代数式概念产生的过程。
2、了解代数式的概念。
3、能分析具体问题中的简单数量关系,并用代数式表示。
学习目标
(1)大米的单价为每千克a元,食用油的单价为每千克b元。买10千克大米、2千克食用油共需_________元。
知识点讲解
请回答下面的问题:
(2)日平均气温是指一天中2:00,8:00,14:00,20:00 四个时刻气温的平均值。若某天上述四个时刻气温的摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数是__________。
(10a+b)
(3)一个五彩花圃的形状如图,花圃的面积为_______。
知识点讲解
请回答下面的问题:
2
思考:上面我们所得到的算式与以前学过的算式有什么区别
知识点讲解
像10a+26, ,2, 这样, 由数、表示数的字母和运算符号组成的数学表达式称为代数式。
这里的运算是指加、減、乘、除、乘方和开方。单独一个数或者一个字母也称代数式。
例1 用代数式表示:
(1)x的3倍与3的差:_________。
(2)x的2倍与y的的和:_________。
(3)a与b的和的平方:________。
(4)2a的立方根:__________。
例题练一练
3x-3
2x+y
知识点讲解
代数式可以简明地、具有普遍意义地表示实际问题中的量,给数量关系的研究带来方便。
例2 一辆汽车以80km/h的速度行驶,从A城到B城需t(h)。如果该车的行驶速度增加v (km/h),那么从A城到B城需多少时间
例题练一练
A城
B城
解:由题意得,A,B两城之间的路程为80t(km)。如果该车的行驶速度增加v(km/h),那么汽车的行驶速度为(80+v)km/h,此时从A城到B城需 (h)。
答:若该车的行驶速度增加v(km/h),则从A城到B城需 (h)。
例题练一练
课内练习
1、用代数式表示:
(1)a与b的的和:_________
(2)a与b的平方的差:_________
(3)m与n的差的平方:_________
(4),和除以s所得的商:_________
(5) x与1的差的平方根:_________
a+
a-
±
课内练习
2、已知甲数比乙数的2倍少1。设乙数为x,用关于x的代数式表示甲数。
解:甲数的表达式是2x-1。
课内练习
3、举一个用代数式 3a+2b表示结果的实际问题的例子。
举例:苹果每千克a元,桃子每千克b元,购买3千克苹果、2千克桃子共需(3a+2b)元。
感悟与反思
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
