4.4 两个三角形相似的判定 导学案

4.4.1 两个三角形相似的判定
班级_________ 学号_________ 姓名_________
一、旧知新证
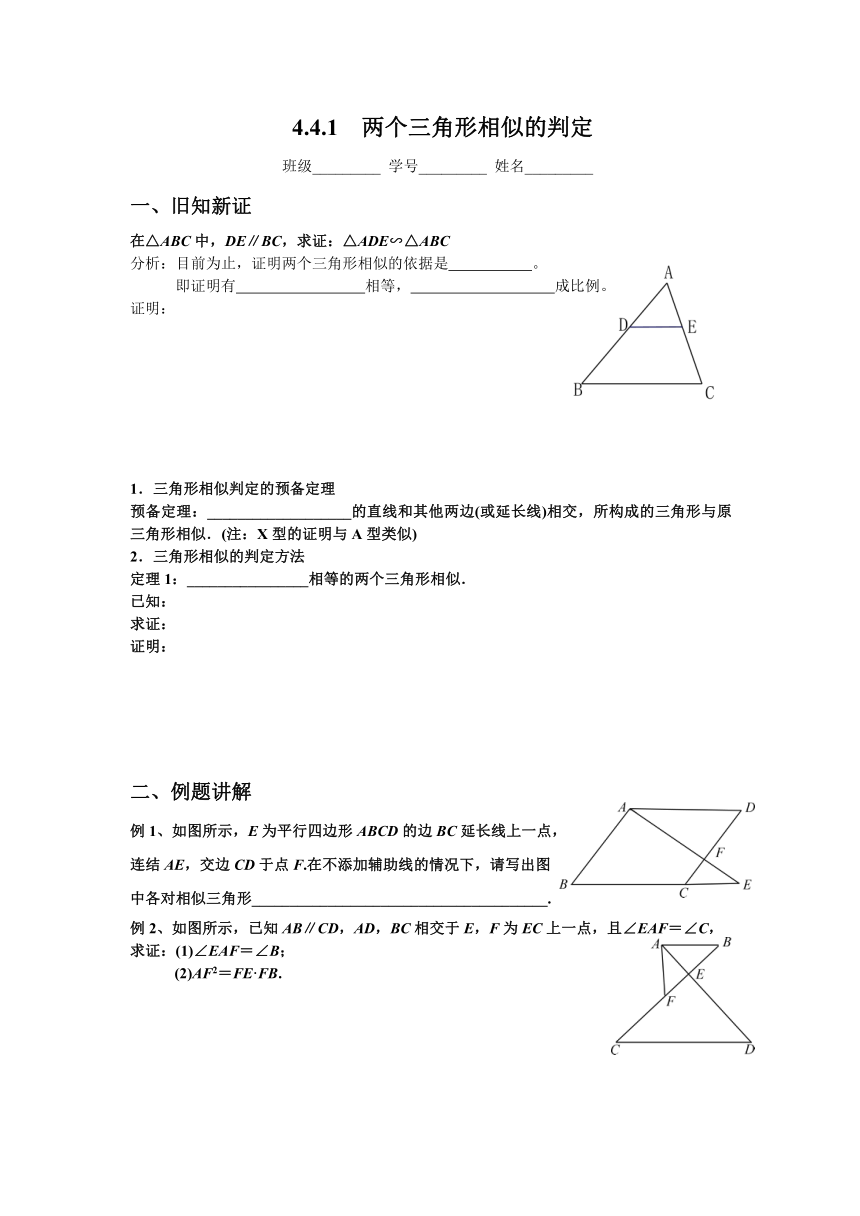
在△ABC中，DE∥BC，求证：△ADE∽△ABC
分析：目前为止，证明两个三角形相似的依据是 。
即证明有 相等， 成比例。
证明：
1．三角形相似判定的预备定理
预备定理：___________________的直线和其他两边(或延长线)相交，所构成的三角形与原三角形相似．(注：X型的证明与A型类似)
2．三角形相似的判定方法
定理1：________________相等的两个三角形相似．
已知：
求证：
证明：
二、例题讲解
例1、如图所示，E为平行四边形ABCD的边BC延长线上一点，
连结AE，交边CD于点F.在不添加辅助线的情况下，请写出图
中各对相似三角形_______________________________________.
例2、如图所示，已知AB∥CD，AD，BC相交于E，F为EC上一点，且∠EAF＝∠C，
求证：(1)∠EAF＝∠B；
(2)AF2＝FE·FB.
巩固练习：
1．如图所示，AB∥CD∥EF，AD，BC相交于点O，找出图中的相似三角形．
2、如图所示，点D是△ABC中AC边上的一点，
(1)若∠1＝__ __时，△CBD∽△CAB； (2)若∠2＝__ __，则△CBD∽△CAB.
3、如图，∠1＝∠2＝∠3，则以下结论不正确的是(　 　)
A．△DEC∽△ABC B．△ADE∽△BEA C．△ACE∽△BEA D．△ACE∽△BCA
4、如图所示，已知DE∥BC，AD＝5，DB＝3，BC＝10，∠B＝50°，则∠ADE＝_______，DE＝_______.
5、如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED＝1，BD＝4，那么AB＝______.
6、如图，点D，E在BC上，且FD∥AB，FE∥AC.求证：△ABC∽△FDE.
7．如图所示，已知⊙O的弦CD垂直于直径AB，点E在CD上，且EC＝EB.
(1)求证：△CEB∽△CBD；
(2)若CE＝3，CB＝5，求DE的长．
8、如图，△ABC内接于⊙O，∠BAC的平分线交⊙O于点D，交边BC于点E，连结BD.
(1)根据题设条件，请你找出图中各对相似三角形；
(2)请选择其中的一对相似三角形加以证明．
第2题图
第1题图
第3题图
第5题图
第4题图